Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 6cm. Lấy điểm M trên cạnh SA sao cho SM = 2MA. Diện tích của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp ( ABC) là: A.
33
23/04/2024
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 6cm. Lấy điểm M trên cạnh SA sao cho \(SM = 2MA\). Diện tích của hình tứ diện khi cắt bởi mặt phẳng qua M và song song với mp \(\left( {ABC} \right)\) là:
A. \(4\sqrt 3 c{m^2}\).
B. \(8\sqrt 3 c{m^2}\).
C. \(\sqrt 3 c{m^2}\).
D. \(16\sqrt 3 c{m^2}\).
Trả lời
Đáp án A
Phương pháp:
Sử dụng tỉ số và định lí Ta-lét.
Cách giải:
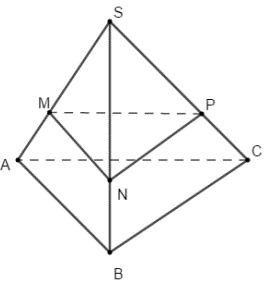
Gọi N, P lần lượt thuộc SB, SC sao cho \(\frac{{SN}}{{SB}} = \frac{{SP}}{{SC}} = \frac{{SM}}{{SA}}\).
Khi đó thiết diện của mặt phẳng qua M song song với \(\left( {ABC} \right)\) là tam giác MNP.
Áp dụng định lí ta-lét trong tam giác SAB có: \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3} = 4\)\(\left( {SM = 2MA;SA = 6} \right)\)
Tương tự ta có \(NP = MP = 4\,cm\).
Do đó tam giác MNP là tam giác đều cạnh 4cm.
\( \Rightarrow {S_{MNP}} = \frac{{\sqrt 3 }}{4}{.4^2} = 4\sqrt 3 c{m^2}\)

