Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh bằng a, SA vuông góc với (ABC) và SA = 2a

Bài 7.28 trang 38 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh bằng a, SA $\perp$ (ABC) và SA = 2a. Tính theo a khoảng cách:

a) Từ điểm B đến mặt phẳng (SAC).

b) Từ điểm A đến mặt phẳng (SBC).

c) Giữa hai đường thẳng AB và SC.

Trả lời

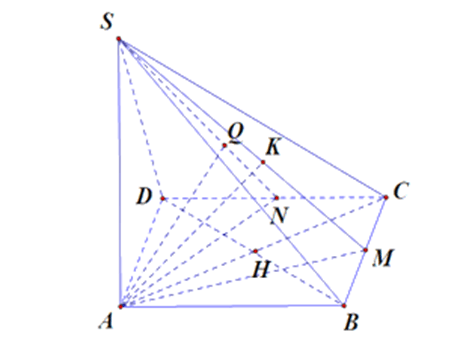
a) Kẻ BH $\perp$ AC tại H.

Vì SA $\perp$ (ABC) nên SA $\perp$ BH mà BH $\perp$ AC. Suy ra, BH $\perp$ (SAC).

Vì ABC là tam giác đều cạnh a có BH là đường cao nên BH = $\frac{a\sqrt{3}}{2}$.

Do đó d(B, (SAC)) = BH = $\frac{a\sqrt{3}}{2}$.

b) Kẻ AM $\perp$ BC tại M, AK $\perp$ SM tại K

Do SA $\perp$ (ABC) nên SA $\perp$ BC mà AM $\perp$ BC nên BC $\perp$ (SAM), suy ra BC $\perp$ AK.

Vì AK $\perp$ SM và BC $\perp$ AK thì AK $\perp$ (SBC).

Suy ra d(A, (SBC)) = AK.

Tam giác ABC đều cạnh bằng a có AM là đường cao nên AM = $\frac{a\sqrt{3}}{2}$.

Vì SA $\perp$ (ABC) nên SA $\perp$ AM.

Xét tam giác SAM vuông tại A, có $\frac{1}{A{K}^2}=\frac{1}{S{A}^2}+\frac{1}{A{M}^2}=\frac{1}{4a^2}+\frac{4}{3a^2}=\frac{19}{12a^2}$ $\Rightarrow$AK = 2a$\sqrt{\frac{3}{19}}$. Vậy d(A, (SBC)) = 2a$\sqrt{\frac{3}{19}}$.

c) Dựng hình bình hành ABCD thì AB // CD nên AB // (SCD) và mặt phẳng (SCD) chứa SC nên d(AB, SC) = d(AB, (SCD)). Mà d(AB, (SCD)) = d(A, (SCD)).

Kẻ AN $\perp$ DC tại N, kẻ AQ $\perp$ SN tại Q

Vì ADC là tam giác đều, AN là đường cao nên AN = $\frac{a\sqrt{3}}{2}$.

Vì SA $\perp$ (ABC) nên SA $\perp$ (ABCD), suy ra SA $\perp$ DC mà AN $\perp$ DC nên DC $\perp$ (SAN).

Vì DC $\perp$ (SAN) nên DC $\perp$ AQ mà AQ $\perp$ SN nên AQ $\perp$ (SDC).

Khi đó d(A, (SCD)) = AQ.

Xét tam giác SAN vuông tại A, có $\frac{1}{A{Q}^2}=\frac{1}{S{A}^2}+\frac{1}{A{N}^2}=\frac{1}{4a^2}+\frac{4}{3a^2}=\frac{19}{12a^2}$
$\Rightarrow AQ=2a\sqrt{\frac{3}{19}}$. Vậy d(AB, SC) = $2a\sqrt{\frac{3}{19}}$ .

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: