Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC bằng 60°, biết tam giác SBC đều

Bài 7.29 trang 38 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC bằng 60°, biết tam giác SBC đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính theo a khoảng cách:

a) Từ điểm S đến mặt phẳng (ABC).

b) Từ điểm B đến mặt phẳng (SAC).

c) Giữa hai đường thẳng AB và SC.

Trả lời

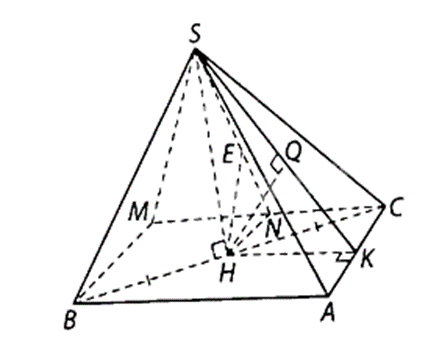
a) Kẻ SH $\perp$ BC tại H. Do (SBC) $\perp$ (ABC) và (SBC) $\cap$ (ABC) = BC nên SH $\perp$ (ABC). Suy ra d(S, (ABC)) = SH.

Vì tam giác SBC là tam giác đều cạnh a, SH là đường cao nên SH = $\frac{a\sqrt{3}}{2}$.

Vậy d(S, (ABC)) = $\frac{a\sqrt{3}}{2}$.

b) Do tam giác SBC đều và SH $\perp$ BC nên SH đồng thời là trung tuyến hay H là trung điểm của BC.

Kẻ HK $\perp$ CA tại K mà SH $\perp$ AC (do SH $\perp$ (ABC)). Suy ra AC $\perp$ (SHK).

Kẻ HQ $\perp$ SK tại Q mà AC $\perp$ HQ (do AC $\perp$ (SHK)). Do đó HQ $\perp$ (SAC).

Khi đó d(H, (SAC)) = HQ.

Xét tam giác vuông ABC vuông tại A, có AB = BC . cos 60° = $\frac{a}{2}$.

Xét tam giác ABC vuông tại A, có HK // AB (vì cùng vuông góc với AC) mà H là trung điểm của BC nên K là trung điểm của AC. Do đó HK là đường trung bình của tam giác ABC. Suy ra HK = $\frac{AB}{2}=\frac{a}{4}$.

Xét tam giác SHK vuông tại H, có $\frac{1}{H{Q}^2}=\frac{1}{S{H}^2}+\frac{1}{H{K}^2}=\frac{4}{3a^2}+\frac{16}{a^2}=\frac{52}{3a^2}$.

$\Rightarrow HQ=\frac{\sqrt{39}a}{26}$.

Lại có H là trung điểm của BC nên d(B, (SAC)) = 2 . d(H, (SAC)) = 2HQ = $\frac{\sqrt{39}a}{13}$.

c) Dựng hình bình hành ABMC mà $\hat{A}=90°$ nên ABMC là hình chữ nhật.

Do ABMC là hình chữ nhật nên AB // MC.

Khi đó AB // (SCM) và mặt phẳng (SCM) chứa SC nên

d(AB, SC) = d(AB, (SCM)) = d(B, (SCM)) = 2d(H, (SCM)).

Kẻ HN $\perp$ CM tại N.

Vì SH $\perp$ (ABC) nên SH $\perp$ (ABMC), suy ra SH $\perp$ MC.

Vì SH $\perp$ MC và HN $\perp$ CM nên CM $\perp$ (SHN).

Kẻ HE $\perp$ SN tại E.

Vì CM $\perp$ (SHN) nên CM $\perp$ HE mà HE $\perp$ SN nên HE $\perp$ (SCM).

Suy ra d(H, (SCM)) = HE.

Xét tam giác vuông ABC vuông tại A, có AC = BC . sin 60° = $\frac{a\sqrt{3}}{2}$.

Xét tam giác BCM có HN là đường trung bình nên HN = $\frac{BM}{2}=\frac{AC}{2}=\frac{a\sqrt{3}}{4}$.

Xét tam giác SHN vuông tại H, có $\frac{1}{H{E}^2}=\frac{1}{S{H}^2}+\frac{1}{H{N}^2}=\frac{4}{3a^2}+\frac{16}{3a^2}=\frac{20}{3a^2}$

$\Rightarrow HE=\frac{\sqrt{15}a}{10}$.

Vậy d(AB, SC) = 2HE $=\frac{\sqrt{15}a}{5}$.