Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 3. Các mặt bên (SAB), (SAC), (SBC) lần lượt tạo với đáy các góc là $30°,45°,60°$ . Tính thể tích của khối chóp S.ABC. Biết rằng hình chiếu vuông góc của S trên (ABC) nằm trong tam giác ABC.

Đáp án đúng là: B

Gọi H là hình chiếu của S lên (ABC).

Đặt SH = h

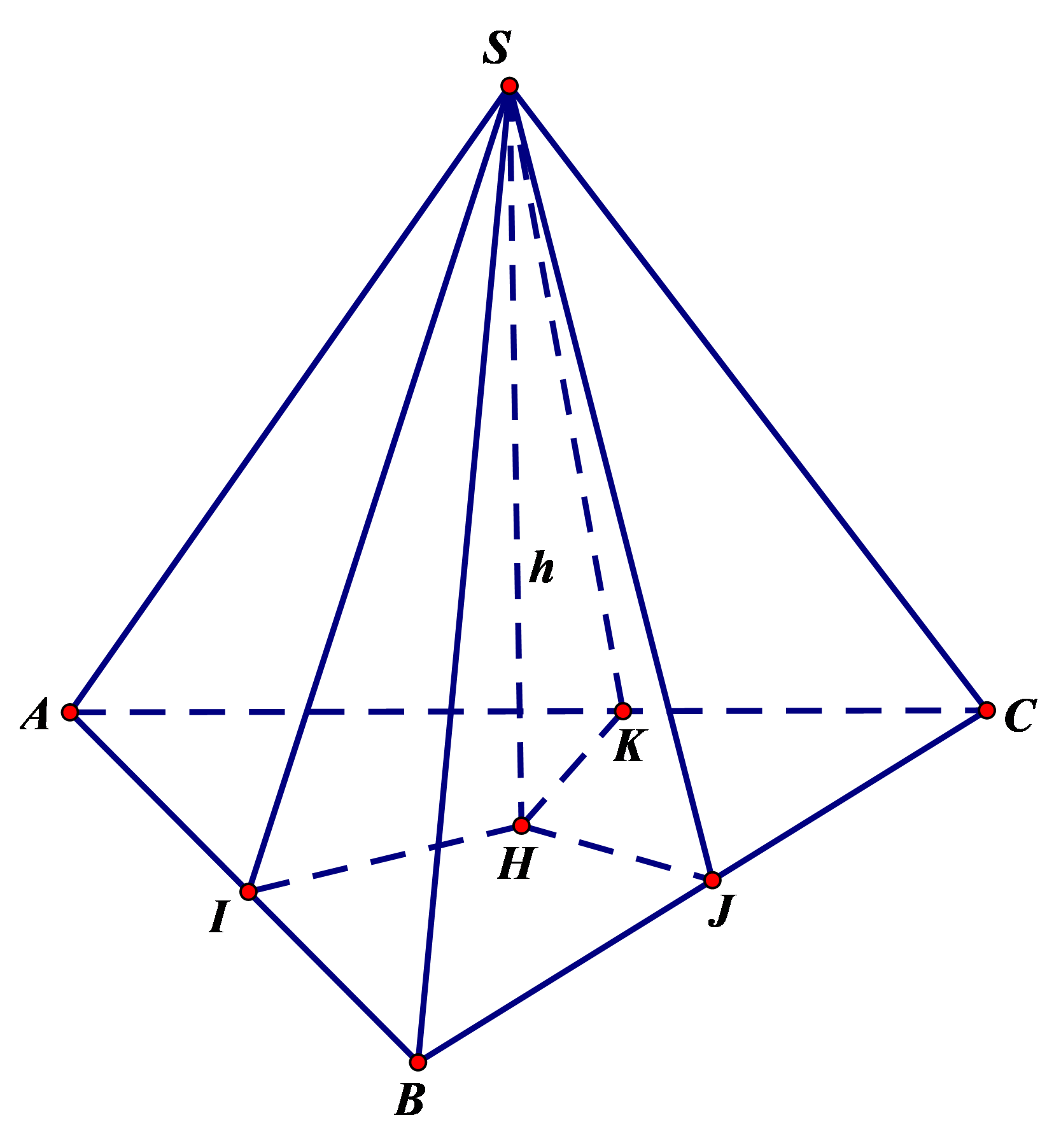
Hạ HI, HJ, HK lần lượt vuông góc với các cạnh AB, BC. AC.

Xét $\Delta SHI$ : $\tan 30°=\frac{SH}{HI}\Rightarrow HI=h\sqrt{3}$

Xét $\Delta SHJ$ : $\tan 60°=\frac{SH}{HJ}\Rightarrow HJ=\frac{h}{\sqrt{3}}$

Xét $\Delta SHK$ : $\tan 45°=\frac{SH}{HK}\Rightarrow HK=h$

Xét $\Delta ABC$ : $S_{ABC}=S_{HAB}+S_{HBC}+S_{HAC}=\frac{1}{2}HI.AB+\frac{1}{2}HJ.BC+\frac{1}{2}HK.AC$

                       $=\frac{1}{2}.h\sqrt{3}.3+\frac{1}{2}.\frac{h}{\sqrt{3}}.3+\frac{1}{2}.h.3=\frac{h\left(4+\sqrt{3}\right)\sqrt{3}}{2}$ .

Mà $S_{ABC}=\frac{\sqrt{3}.A{B}^2}{4}=\frac{\sqrt{3}{.3}^2}{4}$ .

Nên $\frac{h\left(4+\sqrt{3}\right)\sqrt{3}}{2}=\frac{\sqrt{3}{.3}^2}{4}\iff h=\frac{9}{2\left(4+\sqrt{3}\right)}$ .

Vậy $V_{S.ABC}=\frac{1}{3}.h.S_{ABC}=\frac{27\sqrt{3}}{8\left(4+\sqrt{3}\right)}$ .