Cho hình chóp đều S.ABC có $\widehat{ASB}=30°,SA=1$ . Lấy B’, C’ lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác AB’C’ nhỏ nhất. Tỉ số $\frac{V_{S.A{B}^{\text{'}}{C}^{\text{'}}}}{V_{S.ABC}}$  gần giá trị nào nhất trong các giá trị sau?

Đáp án đúng là: C

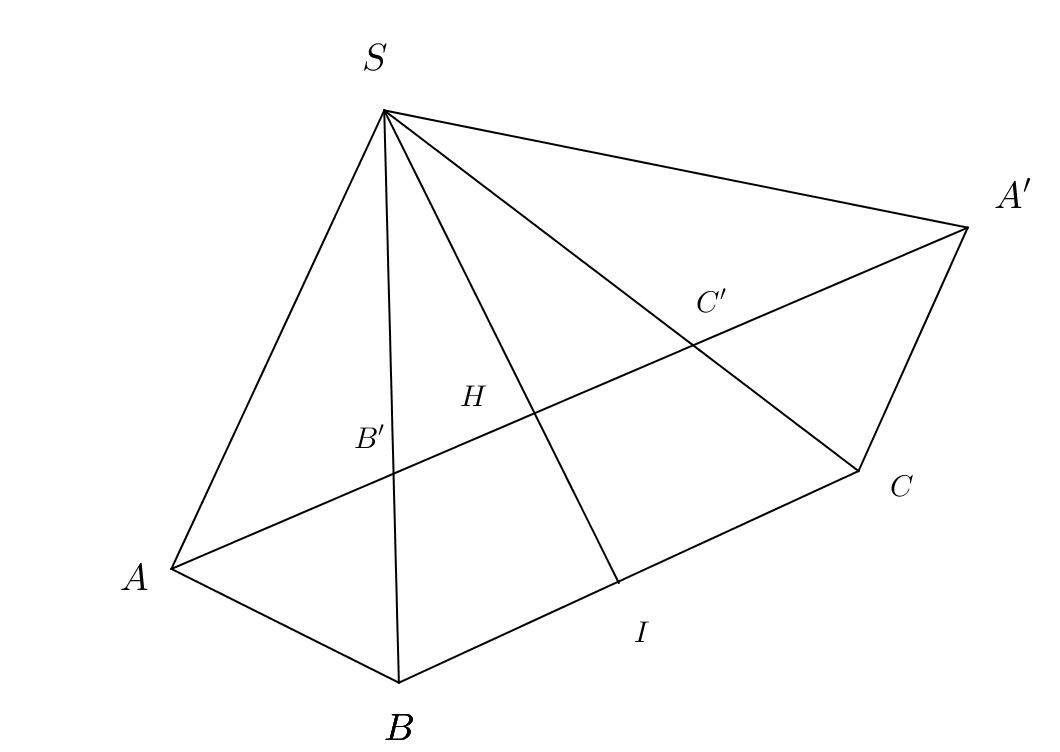
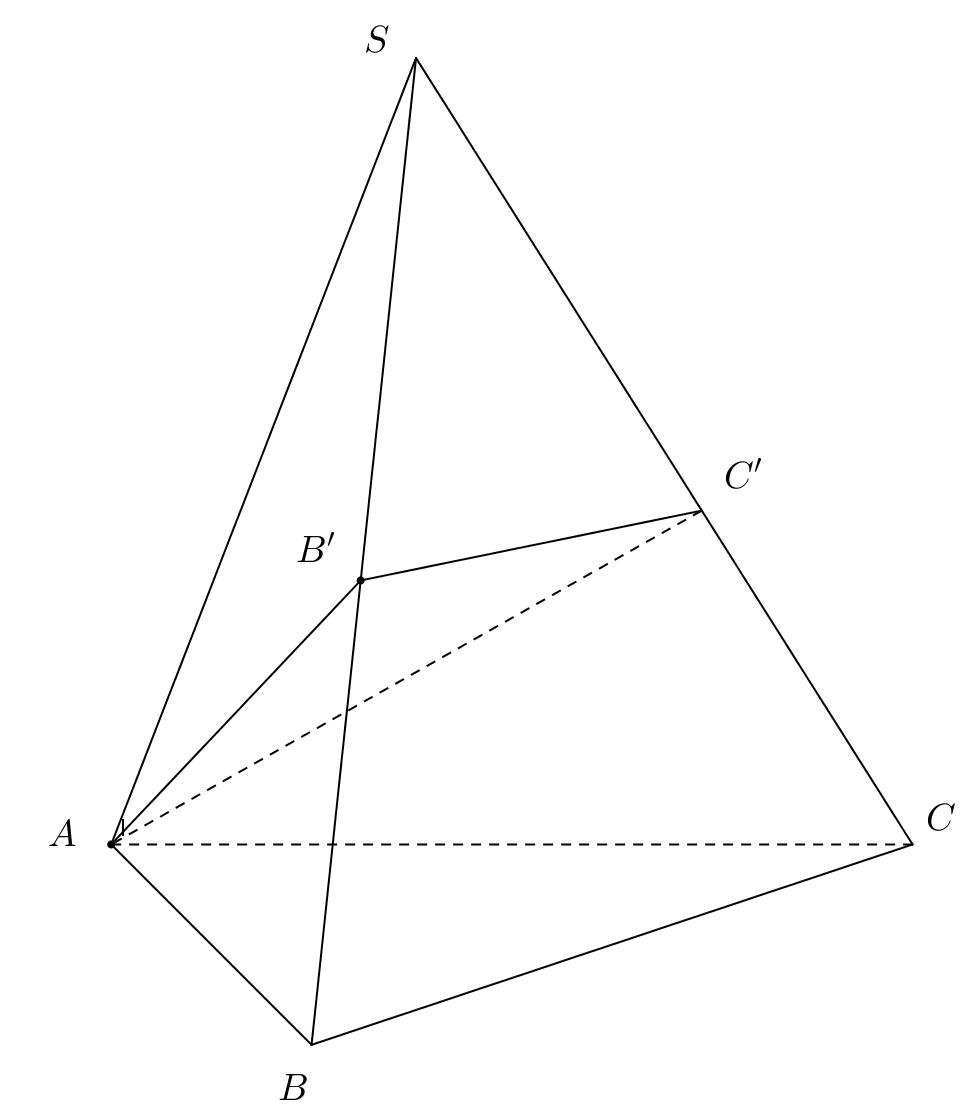
Trải hình, ta có $A\equiv A^{\text{'}},SA=SB=1$ ,$\widehat{ASB}=30°$

$\Rightarrow \Delta SA{A}^{\text{'}}$vuông cân tại S $\Rightarrow \widehat{SA{A}^{\text{'}}}=45°$.

Ta có chu vi $\Delta A{B}^{\text{'}}{C}^{\text{'}}$  là $2p=A{B}^{\text{'}}+A{C}^{\text{'}}+B^{\text{'}}{C}^{\text{'}}\ge A{A}^{\text{'}}$ .

Do đó chu vi $\Delta A{B}^{\text{'}}{C}^{\text{'}}$  nhỏ nhất $\iff B^{\text{'}},C^{\text{'}}\in A{A}^{\text{'}}$.

Gọi I là trung điểm của BC và H là giao điểm của SI và B'C'.

Ta có

$SH=SA.\sin \widehat{SAH}=1.\sin 45°=\frac{\sqrt{2}}{2};SI=SB.\sin \widehat{SBI}=1.\sin 75°=\frac{\sqrt{2}}{4}\left(1+\sqrt{3}\right)$ .

Vì $B^{\text{'}}{C}^{\text{'}}\text{//}BC$  nên $\frac{V_{S.A{B}^{\text{'}}{C}^{\text{'}}}}{V_{S.ABC}}=\frac{S{B}^{\text{'}}}{SB}.\frac{S{C}^{\text{'}}}{SC}=\frac{SH}{SI}.\frac{SH}{SI}={\left(\frac{SH}{SI}\right)}^2=4-2\sqrt{3}$ .

Vậy tỉ số $\frac{V_{S.A{B}^{\text{'}}{C}^{\text{'}}}}{V_{S.ABC}}$  gần giá trị 0,55 nhất trong các giá trị đã cho.