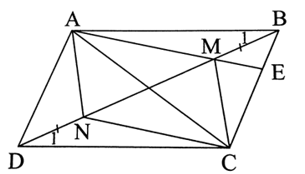
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho BM = DN. a) Chứng minh tứ giác AMCN là hình bình hành. b) Xác định vị trí của điểm M để tia AM cắt BC tại trung điểm củ
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm M và N sao cho BM = DN.
a) Chứng minh tứ giác AMCN là hình bình hành.
b) Xác định vị trí của điểm M để tia AM cắt BC tại trung điểm của BC.