Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc ADB, DBC (E ∈ AB, K ∈ CD). a) Chứng minh DE // BK. b) Giả sử DE ⊥ AB. Chứng minh DA = DB. c) Trong trường hợp DE ⊥
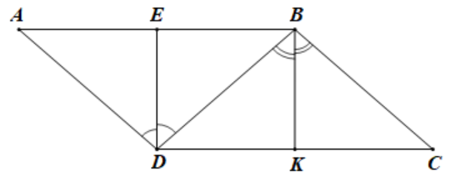
Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của hai góc ^ADB,^DBC(E ∈ AB, K ∈ CD).
a) Chứng minh DE // BK.
b) Giả sử DE ⊥ AB. Chứng minh DA = DB.
c) Trong trường hợp DE ⊥ AB, tìm số đo của ^ADB để tứ giác DEBK là hình vuông.