Bài 3.23 trang 63 Toán 8 Tập 1: Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành;
b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.
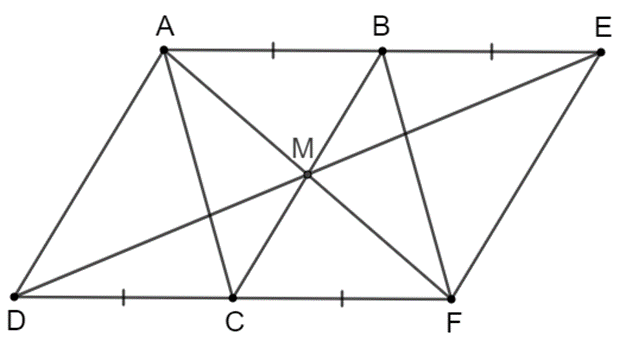
a) Vì ABCD là hình bình hành nên AB = CD; AB // CD.
Mà hai điểm B, C lần lượt là trung điểm AE, DF.
Suy ra AE = DF; AB = BE = CD = CF.
Tứ giác AEFD có AE // DF (vì AB // CD); AE = DF (chứng minh trên).
Do đó tứ giác AEFDlà hình bình hành.
Tứ giác ABFC có AB // CF (vì AB // CD); AB = CF (chứng minh trên).
Do đó tứ giác ABFClà hình bình hành.
Vậy ta chứng minh được hai tứ giác AEFD, ABFC là những hình bình hành.
b) Vì hình bình hành AEFD có hai đường chéo AF và DE nên chúng cắt nhau tại trung điểm của mỗi đường, ta gọi giao điểm đó là O.
Hình bình hành AEFD có hai đường chéo AF và BC.
Mà O là trung điểm của AF.
Suy ra O cũng là trung điểm của BC.
Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.
Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 14: Hình thoi và hình vuông