Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm. Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC

Bài 3.22 trang 63 Toán 8 Tập 1: Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.

a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?

b) Tính khoảng cách từ giao điểm đó đến điểm C.

Trả lời

a)

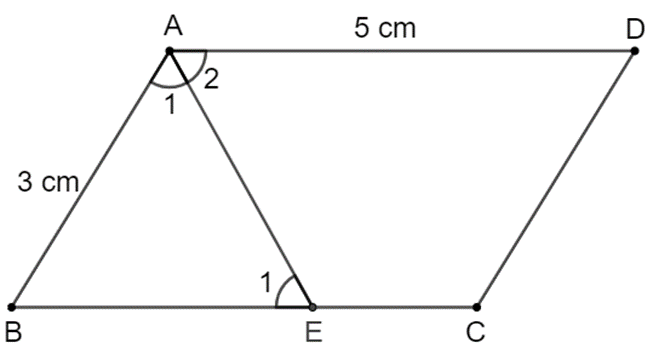
Vì ABCD là hình bình hành nên BC = AD = 5 cm

Do đó có điểm E duy nhất trên cạnh BC sao cho BE = 3 cm.

Tam giác BAE cân tại B (vì BE = BA) nên $\widehat{BAE}=\widehat{BEA}$ mà $\widehat{BEA}=\widehat{EAD}$ (so le trong)

Suy ra $\widehat{BEA}=\widehat{EAD}$ , hay AE là tia phân giác của góc A của hình bình hành ABCD. Tia này không cắt cạnh CD.

b) Gọi E là giao điểm của tia phân giác góc A với cạnh BC.

Khoảng cách từ giao điểm đó đến điểm C tức là khoảng cách từ điểm E đến C, chính là độ dài đoạn EC.

Vì AE là tia phân giác của $\widehat{BAD}$ nên ${\hat{A}}_1={\hat{A}}_2$ .

Vì AD // BC (vì tứ giác ABCD là hình bình hành) nên ${\hat{A}}_2={\hat{E}}_1$ .

Do đó ${\hat{A}}_1={\hat{E}}_1$ .

Tam giác ABE cân tại B (vì ${\hat{A}}_1={\hat{E}}_1$ ) suy ra AB = BE.

Mà AD = BC (vì ABCD là hình bình hành).

Ta có BC = BE + EC.

Suy ra EC = BC – EC = 5 – 3 = 2 (cm).

Vậy EC = 2 cm.

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung

Bài 12: Hình bình hành

Luyện tập chung

Bài 13: Hình chữ nhật

Bài 14: Hình thoi và hình vuông

Luyện tập chung