Cho Hình 4.15, chứng minh rằng ∆ABC = ∆DCB; ∆ADB = ∆DAC
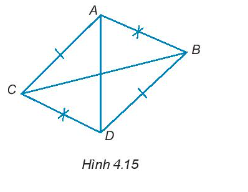
Bài 4.16 trang 57 Tập 1: Cho Hình 4.15, chứng minh rằng ∆ABC = ∆DCB; ∆ADB = ∆DAC.
Xét ∆ABC và ∆DCB có:
AB = DC (giả thiết)
AC = BD (giải thiết)
BC chung
Do đó, ∆ABC = ∆DCB (c – c – c).
Xét hai tam giác ∆ADB và ∆DAC có:
AB = DC (giả thiết)
BD = AC (giải thiết)
AD chung
Do đó, ∆ADB = ∆DAC (c – c – c).
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 12: Tổng các góc trong một tam giác
Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác