Cho hàm số y = f(x) = ax^2 + bx + c với đồ thị là parabol (P) có đỉnh (5/2;-1/4) và đi qua điểm A(1; 2)

Bài 9 trang 96 Toán 10 Tập 2: Cho hàm số y = f(x) = ax² + bx + c với đồ thị là parabol (P) có đỉnh$I\left(\frac{5}{2};-\frac{1}{4}\right)$ và đi qua điểm A(1; 2).

a) Biết rằng phương trình của parabol có thể viết dưới dạng y = a(x – h)² + k, trong đó I(h, k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.

b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

c) Giải bất phương trình f(x) ≥ 0.

Trả lời

a) Vì parabol có đỉnh $I\left(\frac{5}{2};-\frac{1}{4}\right)$ nên ta có h =$\frac{5}{2}$ và k =$-\frac{1}{4}$ . Suy ra phương trình của parabol (P) có dạng: $y=a{\left(x-\frac{5}{2}\right)}^2-\frac{1}{4}$. 

Vì parabol (P) đi qua điểm A(1; 2) nên ta có $2=a{\left(1-\frac{5}{2}\right)}^2-\frac{1}{4}$. Suy ra a = 1. 

Vậy parabol (P) có phương trình là $y=1.{\left(x-\frac{5}{2}\right)}^2-\frac{1}{4}$ hay y = x² – 5x + 6. 

* Vẽ parabol (P): 

Parabol có đỉnh $I\left(\frac{5}{2};-\frac{1}{4}\right)$, hệ số a = 1> 0 nên parabol có bề lõm hướng lên trên.

Phương trình trục đối xứng: $x=\frac{5}{2}$. 

Giao điểm của (P) với trục tung có tọa độ là B(0; 6). 

Phương trình x² – 5x + 6 = 0 có hai nghiệm x = 2 và x = 3. Vậy giao điểm của (P) với trục hoành là C(2; 0) và D(3; 0). 

Vẽ đường cong đi qua các điểm trên ta được parabol (P).

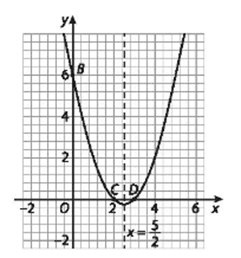
b) Từ parabol (P) đã vẽ ở câu a, ta có hàm số y = x² – 5x + 6 đồng biến trên khoảng $\left(\frac{5}{2};+\infty \right)$ và nghịch biến trên khoảng $\left(-\infty ;\frac{5}{2}\right)$. 

c) Ta có: f(x) ≥ 0 

⇔ x² – 5x + 6 ≥ 0

⇔ x ≤ 2 hoặc x ≥ 3 (từ đồ thị suy ra)

Vậy tập nghiệm của bất phương trình là S = (– ∞; 2] ∪ [3; + ∞).