Cho hàm số f( x ) = 1 + 2/x - 1 có đồ thị như Hình 5.4. Giả sử (xn) là dãy số sao cho xn > 1, xn ⟶ +∞. Tính f(xn) và tìm lim n đến + vô cùng f( xn).
21
26/07/2024
Cho hàm số \(f\left( x \right) = 1 + \frac{2}{{x - 1}}\) có đồ thị như Hình 5.4.
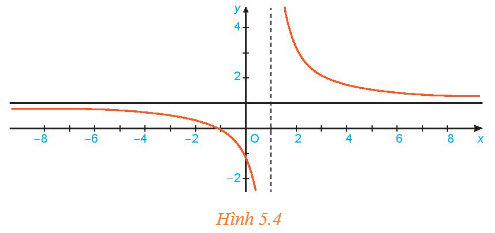
Giả sử (xn) là dãy số sao cho xn > 1, xn ⟶ +∞. Tính f(xn) và tìm \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right)\).
Trả lời
Lời giải:
Với (xn) là dãy số sao cho xn > 1, xn ⟶ +∞.
Ta có: \(f\left( {{x_n}} \right) = 1 + \frac{2}{{{x_n} - 1}}\).
Khi xn ⟶ +∞ thì \(\mathop {\lim }\limits_{n \to + \infty } \frac{2}{{{x_n} - 1}} = 0\).
Do đó \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right) = \mathop {\lim }\limits_{n \to + \infty } \left( {1 + \frac{2}{{{x_n} - 1}}} \right) = 1\).
