Cho hai tam giác ABC và A'B'C' có \[\widehat A = \widehat {A'},\;\widehat C = \widehat {C'}\] (Hình 9).

Trên cạnh AC, Lấy điểm D sao cho DC = A'C'. Qua D kẻ đường thẳng song song với AB cắt cạnh BC tại E.

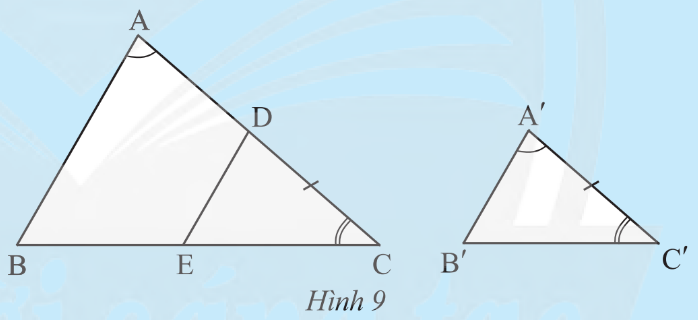
a) Tam giác DEC có đồng dạng với tam giác ABC không?

b) Nhận xét về mối quan hệ giữa tam giác A'B'C' và tam giác DEC.

c) Dự đoán về sự đồng dạng của hai tam giác A'B'C' và ABC.

Lời giải:

a) Tam giác ABC có DE // AB nên ΔDEC ᔕ ΔABC.

b) ΔDEC ᔕ ΔABC, do đó \[\widehat D = \widehat A\]

Xét ΔA′B′C và ΔDEC có:

\[\widehat {A'} = \widehat D\] (cùng bằng \[\widehat A\])

A'C' = DC (gt)

\[\widehat {C'} = \widehat C\] (gt)

Suy ra ΔA′B′C′ = ΔDEC (g.c.g).

c) Từ câu b, ta có: ΔA′B′C′ = ΔDEC.

Dự đoán: ΔA′B′C′ ᔕ ΔABC.