Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC = 3AB, B′D′ = 3A′B′

Bài 9.26 trang 103 Toán 8 Tập 2: Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC = 3AB, B′D′ = 3A′B′.

a) Chứng minh rằng ΔABC ∽ ΔA'B'C'.

b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là 2 m² thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu?

Trả lời

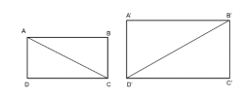
a) Ta có AC = 3AB. Suy ra $\frac{AB}{AC}=\frac{1}{3}$ .

- Có B′D′ = 3A′B′. Suy ra $\frac{A\text{'}B\text{'}}{B\text{'}D\text{'}}=\frac{1}{3}$ .

Do đó, $\frac{AB}{AC}=\frac{A\text{'}B\text{'}}{B\text{'}D\text{'}}$, suy ra  $\frac{AB}{A\text{'}B\text{'}}=\frac{AC}{B\text{'}D\text{'}}$.

Mà A'B'C'D' là hình chữ nhật nên A'C' = B'D', do đó $\frac{AB}{A\text{'}B\text{'}}=\frac{AC}{A\text{'}C\text{'}}$ .

Xét tam giác vuông ABC (vuông tại B) và tam giác vuông A'B'C' (vuông tại B') có

$\frac{AB}{A\text{'}B\text{'}}=\frac{AC}{A\text{'}C\text{'}}$.

Suy ra ΔABC ∽ ΔA′B′C′ (cạnh huyền – cạnh góc vuông).

b) Vì A′B′ = 2AB. Suy ra  $\frac{AB}{A\text{'}B\text{'}}=\frac{1}{2}$.

Mà ΔABC ∽ ΔA'B'C'. Suy ra  $\frac{AC}{A\text{'}C\text{'}}=\frac{BC}{B\text{'}C\text{'}}=\frac{AB}{A\text{'}B\text{'}}=\frac{1}{2}$.

+ Ta có diện tích hình chữ nhật ABCD là: AB ∙ BC

+ Diện tích hình chữ nhật A'B'C'D' là: A′B′ ∙ B′C′.

Xét tỉ lệ diện tích hai hình chữ nhật ABCD và A'B'C'D', có

$\frac{AB\cdot BC}{A\text{'}B\text{'}\cdot BC}=\frac{AB}{A\text{'}B\text{'}}\cdot \frac{BC}{B\text{'}C\text{'}}=\frac{1}{2}\cdot \frac{1}{2}=\frac{1}{4}$.

Suy ra A′B′ ∙ B′C′ = 4AB ∙ BC = 4 ∙ 2 = 8 m².

Vậy diện tích hình chữ nhật A'B'C'D' là 8 m².

Xem thêm lời giải bài tập SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung (trang 91)

Bài 35: Định lí Pythagore và ứng dụng

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng

Luyện tập chung (trang 108)

Bài tập cuối chương 9