Cho ΔA'B'C' ∽ ΔABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC

Bài 9.27 trang 103 Toán 8 Tập 2: Cho ΔA'B'C' ∽ ΔABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC.

Chứng minh rằng:

a)$\frac{A\text{'}H\text{'}}{AH}=k$.

b) Diện tích tam giác A'B'C' bằng k² lần diện tích tam giác ABC.

Trả lời

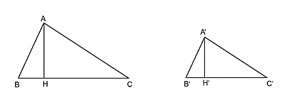
a) Vì ΔA'B'C' ∽ ∆ABC theo tỉ số k nên $\widehat{B}=\widehat{B\text{'}};\frac{A\text{'}B\text{'}}{AB}=\frac{A\text{'}C\text{'}}{AC}=\frac{B\text{'}C\text{'}}{BC}=k$ .

Xét tam giác A'H'B' vuông tại H' và tam giác AHB vuông tại H có: $\widehat{B}=\widehat{B\text{'}}$ .

Do đó ∆A'H'B' ∽ ∆AHB.

Suy ra $\frac{A\text{'}H\text{'}}{AH}=\frac{A\text{'}B\text{'}}{AB}=k$.

b) Diện tích tam giác ABC là $\frac{1}{2}\cdot AH\cdot BC$

Diện tích tam giác A'B'C' là $\frac{1}{2}\cdot A\text{'}H\text{'}\cdot B\text{'}C\text{'}$

Xét tỉ lệ diện tích giữa hai tam giác A'B'C' và tam giác ABC:

$\frac{\frac{1}{2}A\text{'}H\text{'}\cdot B\text{'}C\text{'}}{\frac{1}{2}AH\cdot BC}=\frac{A\text{'}H\text{'}}{AH}\cdot \frac{B\text{'}C\text{'}}{BC}=k\cdot k=k^2$ Suy ra $\frac{1}{2}A\text{'}H\text{'}\cdot B\text{'}C\text{'}=k^2\cdot \frac{1}{2}AH\cdot BC$ .

Vậy diện tích tam giác A'B'C' bằng k² lần diện tích tam giác ABC.

Xem thêm lời giải bài tập SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung (trang 91)

Bài 35: Định lí Pythagore và ứng dụng

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng

Luyện tập chung (trang 108)

Bài tập cuối chương 9