Các tam giác vuông AHB và A'H'B' trong Hình 9.50 mô tả hai con dốc có chiều dài lần lượt là AB = 13 m, A′B′ = 6,5 m

HĐ1 trang 100 Toán 8 Tập 2: Các tam giác vuông AHB và A'H'B' trong Hình 9.50 mô tả hai con dốc có chiều dài lần lượt là AB = 13 m, A′B′ = 6,5 m và độ cao lần lượt là BH = 5 m, B′H′ = 2,5 m. Độ dốc của hai con dốc lần lượt được tính bởi số đo các góc HAB và H'A'B'.

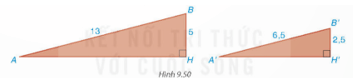
- Nhận xét về hai đại lượng $\frac{A\text{'}B\text{'}}{AB}và\frac{B\text{'}H\text{'}}{BH}$ .

- Dùng định lí Pythagore để tính AH và A'H'.

- So sánh các đại lượng  $\frac{A\text{'}H\text{'}}{AH}và\frac{B\text{'}H\text{'}}{BH}$.

- Hai tam giác vuông A'H'B' và AHB có đồng dạng không? Từ đó rút ra kết luận về độ dốc của hai con dốc.

Trả lời

- Ta có: $\frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}H\text{'}}{BH}=\frac{1}{2}$ .

- Áp dụng định lí Pythagore cho tam giác vuông ABH ta có: AH² + BH² = AB², suy ra AH² = AB² – BH² = 13² – 5² = 144.

Suy ra AH = 12 (m).

- Tương tự ta có: A'H'² = A'B'² – B'H'² = (6,5)² – (2,5)² = 36. Suy ra A'H' = 6 (m).

- Vậy $\frac{A\text{'}H\text{'}}{AH}=\frac{1}{2}=\frac{B\text{'}H\text{'}}{BH}$ .

Do đó hai tam giác vuông A'H'B' và AHB đồng dạng, suy ra $\widehat{A}=\widehat{A\text{'}}$ .

Vậy hai con dốc có độ dốc như nhau.

Xem thêm lời giải bài tập SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung (trang 91)

Bài 35: Định lí Pythagore và ứng dụng

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng

Luyện tập chung (trang 108)

Bài tập cuối chương 9