Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD

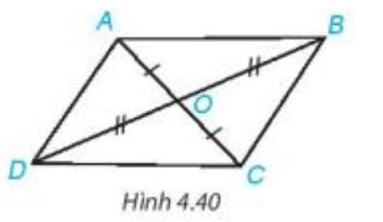
Bài 4.13 trang 73 Toán 7 Tập 1: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.

a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.

b) Chứng minh rằng $\Delta DAB=\Delta BC\text{D}.$

Trả lời

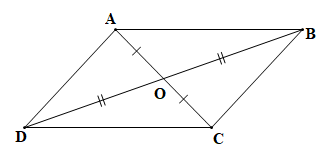
a) Hai cặp tam giác có chung đỉnh O bằng nhau là:

 +) Tam giác OAB và tam giác OCD

Giải thích:

OA = OC (giải thuyết)

OB = OD (giải thuyết)

$\widehat{AOB}=\widehat{COD}$ (hai góc đối đỉnh)

Do đó, $\Delta OAB=\Delta OCD$ (c – g – c)

+) Tam giác OAD và tam giác OCB.

Giải thích:

OA = OC (giải thuyết)

OD = OB (giải thuyết)

$\widehat{AOD}=\widehat{COB}$ (hai góc đối đỉnh)

Do đó, $\Delta OAD=\Delta OCB$ (c – g – c)

b) $\Delta OAB=\Delta OCD$ (Chứng minh ở câu a) nên $\widehat{ABO}=\widehat{CDO}$ (hai góc tương ứng) hay $\widehat{ABD}=\widehat{CDB}.$ 

$\Delta OAD=\Delta OCB$(Chứng minh ở câu a) nên $\widehat{ADO}=\widehat{CBO}$ (hai góc tương ứng) hay $\widehat{ADB}=\widehat{CBD}.$ 

+) Xét tam giác DAB và tam giác BCD có:

$\widehat{ABD}=\widehat{CDB}$ (chứng minh trên);

BD là cạnh chung;

$\widehat{ADB}=\widehat{CBD}$ (chứng minh trên).

Vậy $\Delta DAB=\Delta BCD$ (g.c.g).

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Luyện tập chung trang 68

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Luyện tập chung trang 74

Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng