Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC

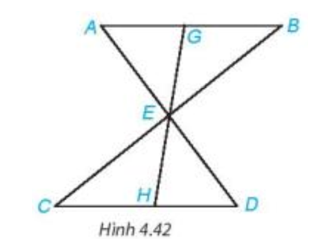
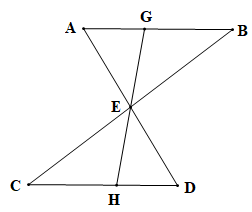
Bài 4.15 trang 73 Toán 7 Tập 1: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:

a) $\Delta ABE=\Delta DCE;$                             

b) EG = EH.

Trả lời

a) Từ AB // CD (theo giả thiết) suy ra $\widehat{DAB}=\widehat{ADC}$ (hai góc so le trong) và $\widehat{ABC}=\widehat{DCB}$ (hai góc so le trong).

Hay $\widehat{EAB}=\widehat{EDC}$ và $\widehat{ABE}=\widehat{DCE}.$

Xét tam giác ABE và tam giác DCE có:

$\widehat{EAB}=\widehat{EDC}$ (chứng minh trên);

AB = DC (theo giả thiết);

$\widehat{ABE}=\widehat{DCE}$ (chứng minh trên).

Vậy $\Delta ABE=\Delta DCE$ (g.c.g).

b) Từ $\Delta ABE=\Delta DCE$(chứng minh câu a) suy ra AE = DE (hai cạnh tương ứng).

Xét tam giác AEG và tam giác DEH có:

$\widehat{EAG}=\widehat{EDH}$ (do $\widehat{EAB}=\widehat{EDC}$);

AE = DE (chứng minh trên);

$\widehat{AEG}=\widehat{DEH}$ (hai góc đối đỉnh).

Vậy $\Delta AEG=\Delta DEH$ (g.c.g).

Suy ra EG = EH (hai cạnh tương ứng).

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Luyện tập chung trang 68

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Luyện tập chung trang 74

Bài 15: Các trường hợp bằng nhau của tam giác vuông

Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng