Câu hỏi:
29/12/2023 184Cho hai điểm A(2; 2), B(5; 1) và đường thẳng ∆: x – 2y + 8 = 0. Lấy điểm C ∈ ∆. Điểm C có hoành độ dương sao cho diện tích tam giác ABC bằng 17. Tọa độ của C là:
A. C(10; 12);
B. C(12; 10);
C. C(8; 8);
D. C(10; 8).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
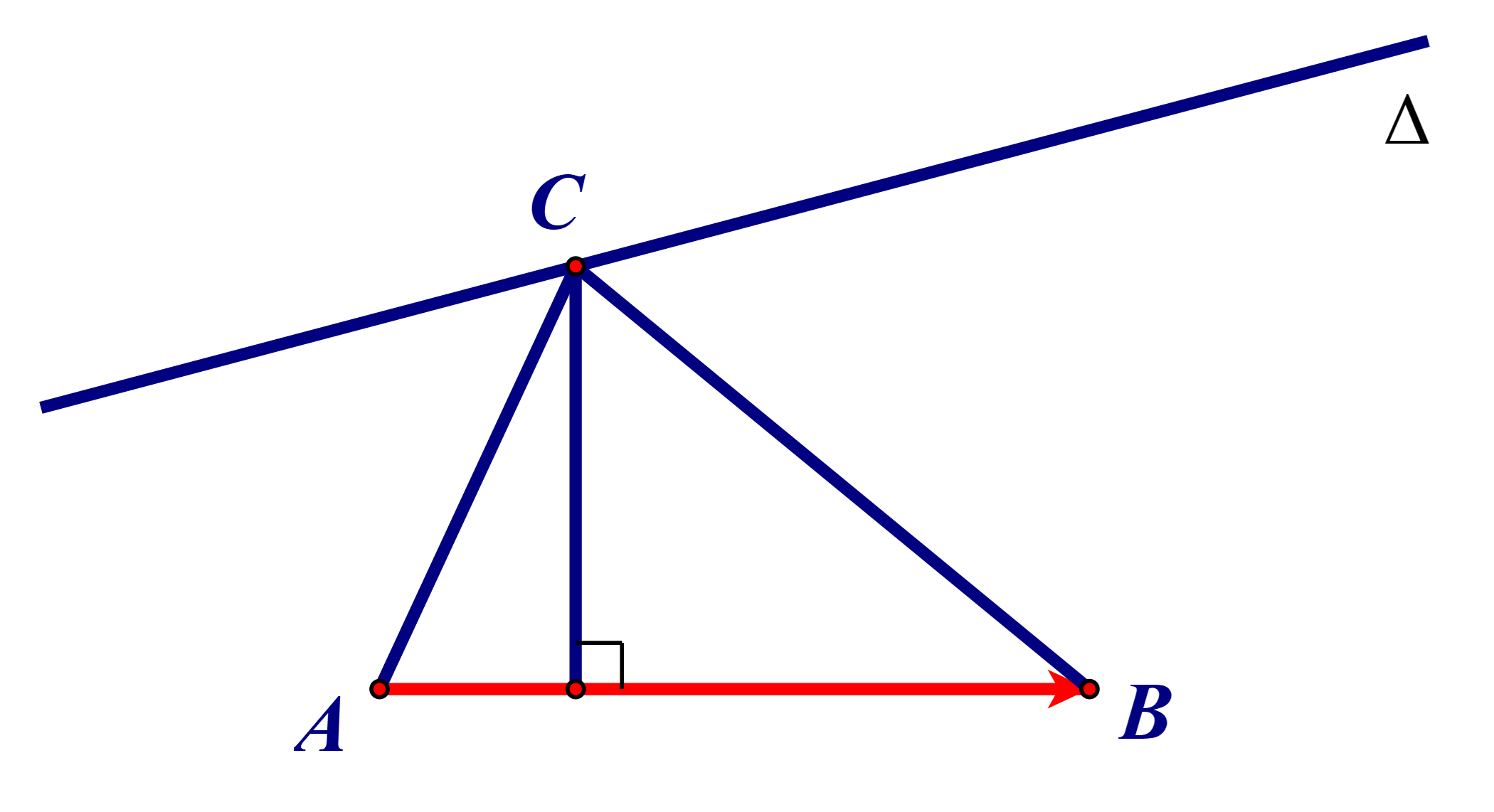
Ta có \(\overrightarrow {AB} = \left( {3; - 1} \right)\). Suy ra \(AB = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} \).
Đường thẳng AB có vectơ chỉ phương \(\overrightarrow {AB} = \left( {3; - 1} \right)\).
Suy ra đường thẳng AB có vectơ pháp tuyến \({\vec n_{AB}} = \left( {1;3} \right)\).
Đường thẳng AB đi qua A(2; 2) và có vectơ chỉ phương \(\overrightarrow {AB} = \left( {3; - 1} \right)\).
Suy ra phương trình tổng quát của AB: 1(x – 2) + 3(y – 2) = 0.
⇔ x + 3y – 8 = 0.
Đường thẳng ∆ đi qua điểm M(–8; 0) và có vectơ chỉ phương \({\vec u_\Delta } = \left( {2;1} \right)\).
Suy ra phương trình tham số của ∆: \(\left\{ \begin{array}{l}x = - 8 + 2t\\y = t\end{array} \right.\)
Ta có C ∈ ∆. Suy ra tọa độ C(2t – 8; t).
Theo đề, ta có diện tích tam giác ABC bằng 17.
\( \Leftrightarrow \frac{1}{2}d\left( {C,AB} \right).AB = 17\).
\( \Leftrightarrow \frac{1}{2}.\frac{{\left| {2t - 8 + 3t - 8} \right|}}{{\sqrt {{1^2} + {3^2}} }}.\sqrt {10} = 17\)
⇔ |5t – 16| = 34
\( \Leftrightarrow \left[ \begin{array}{l}5t - 16 = 34\\5t - 16 = - 34\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}t = 10\\t = - \frac{{18}}{5}\end{array} \right.\)
Với t = 10, ta có C(12; 10).
Với \(t = - \frac{{18}}{5}\), ta có \(C\left( { - \frac{{76}}{5}; - \frac{{18}}{5}} \right)\).
Vậy C(12; 10) hoặc \(C\left( { - \frac{{76}}{5}; - \frac{{18}}{5}} \right)\) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án B.
Hướng dẫn giải
Đáp án đúng là: B

Ta có \(\overrightarrow {AB} = \left( {3; - 1} \right)\). Suy ra \(AB = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10} \).
Đường thẳng AB có vectơ chỉ phương \(\overrightarrow {AB} = \left( {3; - 1} \right)\).
Suy ra đường thẳng AB có vectơ pháp tuyến \({\vec n_{AB}} = \left( {1;3} \right)\).
Đường thẳng AB đi qua A(2; 2) và có vectơ chỉ phương \(\overrightarrow {AB} = \left( {3; - 1} \right)\).
Suy ra phương trình tổng quát của AB: 1(x – 2) + 3(y – 2) = 0.
⇔ x + 3y – 8 = 0.
Đường thẳng ∆ đi qua điểm M(–8; 0) và có vectơ chỉ phương \({\vec u_\Delta } = \left( {2;1} \right)\).
Suy ra phương trình tham số của ∆: \(\left\{ \begin{array}{l}x = - 8 + 2t\\y = t\end{array} \right.\)
Ta có C ∈ ∆. Suy ra tọa độ C(2t – 8; t).
Theo đề, ta có diện tích tam giác ABC bằng 17.
\( \Leftrightarrow \frac{1}{2}d\left( {C,AB} \right).AB = 17\).
\( \Leftrightarrow \frac{1}{2}.\frac{{\left| {2t - 8 + 3t - 8} \right|}}{{\sqrt {{1^2} + {3^2}} }}.\sqrt {10} = 17\)
⇔ |5t – 16| = 34
\( \Leftrightarrow \left[ \begin{array}{l}5t - 16 = 34\\5t - 16 = - 34\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}t = 10\\t = - \frac{{18}}{5}\end{array} \right.\)
Với t = 10, ta có C(12; 10).
Với \(t = - \frac{{18}}{5}\), ta có \(C\left( { - \frac{{76}}{5}; - \frac{{18}}{5}} \right)\).
Vậy C(12; 10) hoặc \(C\left( { - \frac{{76}}{5}; - \frac{{18}}{5}} \right)\) thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(3; 4), B(2; 1), C(–1; –2). Cho M(x; y) trên đoạn thẳng BC sao cho SABC = 4SABM. Khi đó x2 – y2 bằng:
Câu 2:
Cho đường tròn (C): x2 + y2 + 2x – 6y + 5 = 0. Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y – 15 = 0 là:
Câu 3:
Cho điểm M nằm trên ∆: x + y – 1 = 0 và cách N(–1; 3) một khoảng bằng 5. Khi đó tọa độ điểm M là:
Câu 4:
Cho elip (E): \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Đường thẳng d: x = –4 cắt (E) tại hai điểm M, N. Khi đó:


