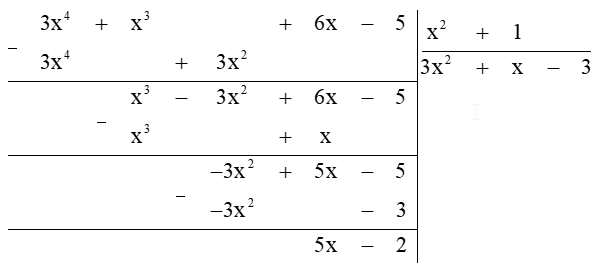Bài 7.29 trang 34 SBT Toán 7 Tập 2: Cho hai đa thức A = 3x4 + x3 + 6x −5 và B = x2 + 1. Tìm thương Q và dư R trong phép chia A cho B rồi kiểm nghiệm lại rằng A = BQ + R.
Thực hiện phép chia (3x4 + x3 + 6x −5) : (x2 + 1)
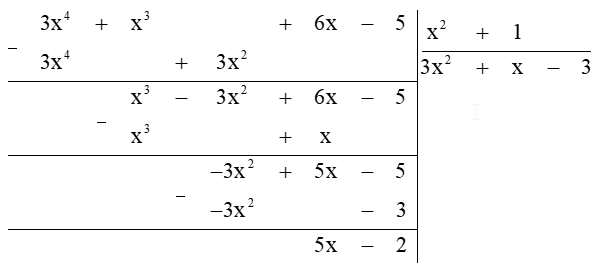
Vậy phép chia (3x4 + x3 + 6x −5) : (x2 + 1) có thương Q = 3x2 + x − 3 và dư R = 5x − 2
Kiểm nghiệm BQ + R = (x2 + 1)(3x2 + x − 3) + 5x − 2
= x2( 3x2 + x − 3) + 1. (3x2 + x − 3) + 5x − 2
= 3x4 + x3 − 3x2 + 3x2 + x − 3 + 5x − 2
= 3x4 + x3 + (−3x2 + 3x2) + (x + 5x) + (−3 − 2)
= 3x4 + x3 + 6x −5 = A
Vậy A = BQ + R là một đẳng thức đúng.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 26: Phép cộng và phép trừ đa thức một biến
Bài 27: Phép nhân đa thức một biến