Cho chóp tứ giác S.ABCD có đáy là hình bình hành (tham khảo hình vẽ). Gọi I, J, K lần lượt là trung điểm các cạnh SA, SB, SC. Mệnh đề nào sau đây là mệnh đề sai? A. IJ//CD B. SD ( IJK)
36
24/04/2024
Cho chóp tứ giác \(S.ABCD\) có đáy là hình bình hành (tham khảo hình vẽ). Gọi I, J, K lần lượt là trung điểm các cạnh SA, SB, SC. Mệnh đề nào sau đây là mệnh đề sai?
A. \(IJ//CD\)
B. \(SD \cap \left( {IJK} \right) = \emptyset \)
C. \(\left( {IJK} \right) \cap \left( {ACD} \right) = \emptyset \)
D. \(IK//AC\)
Trả lời
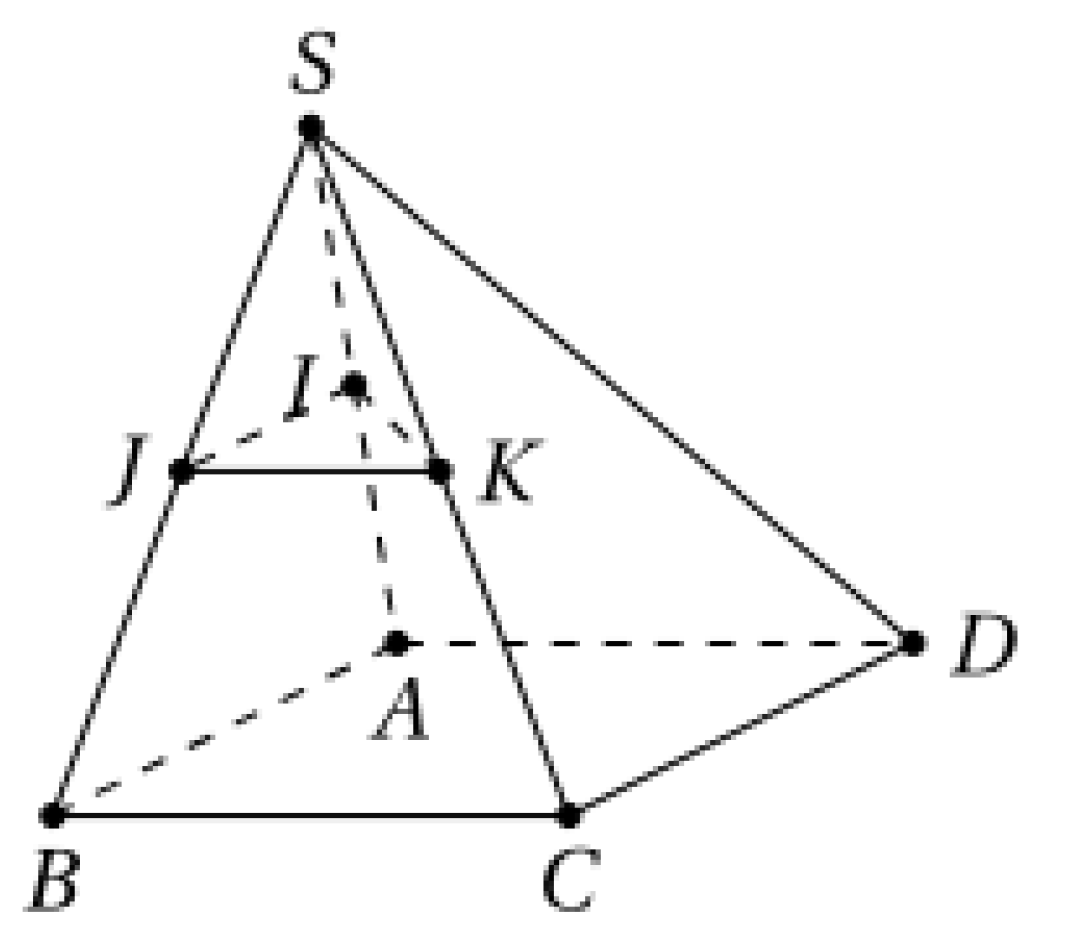
Đáp án B
Phương pháp:
Sử dụng tính chất hình bình hành, tính chất đường trung bình của tam giác
Sử dụng cách tìm giao tuyến của hai mặt phẳng, tìm giao điểm của đường thẳng và mặt phẳng.
Cách giải:
Vì \(ABCD\) là hình bình hành nên \(AB//CD\), lại có \(IJ//AB\) (do \(IJ\) là đường trung bình của tam giác \(SAB\)) nên \(IJ//CD\) hay A đúng.
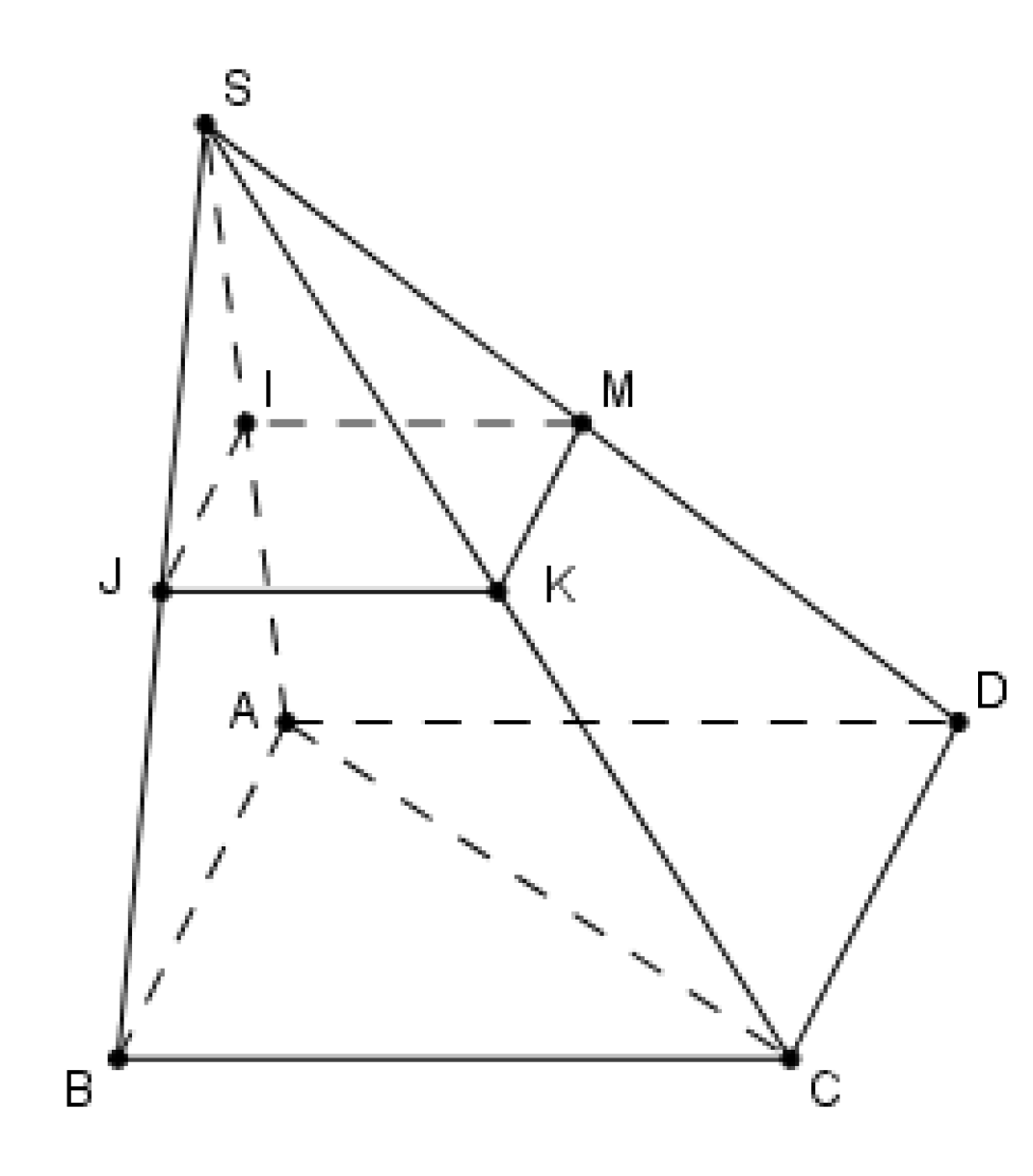
Lấy \(M\) là trung điểm của \(SD \Rightarrow IJKM\) là hình bình hành nên \(\left( {IJK} \right) \cap SD = \left\{ M \right\}\), do đó B sai.
Vì \(\left\{ \begin{array}{l}IJ//AB\\JK//BC\end{array} \right. \Rightarrow \left( {IJK} \right)//\left( {ACD} \right)\) nên \(\left( {IJK} \right) \cap \left( {ACD} \right) = \emptyset \), do đó C đúng.
+ \(IK//AC\) do \(IK\) là đường trung bình tam giác \(SAC\) nên D đúng.
