Câu hỏi:
19/01/2024 46
Cho bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0. Để x = 6 là một nghiệm của bất phương trình trên thì m nhận giá trị nào trong các giá trị sau đây?
Cho bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0. Để x = 6 là một nghiệm của bất phương trình trên thì m nhận giá trị nào trong các giá trị sau đây?
A. ;
A. ;
Đáp án chính xác
B. ;
B. ;
C. ;
D. .
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Vì x = 6 là một nghiệm của bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0 nên ta có:
(m – 2).62 + 2(2m – 3).6 + 5m – 6 ≥ 0.
⇔ 36(m – 2) + 12(2m – 3) + 5m – 6 ≥ 0
⇔ 65m – 114 ≥ 0
Vậy thỏa mãn yêu cầu bài toán.
Ta chọn phương án A.
Hướng dẫn giải
Đáp án đúng là: A
Vì x = 6 là một nghiệm của bất phương trình (m – 2)x2 + 2(2m – 3)x + 5m – 6 ≥ 0 nên ta có:
(m – 2).62 + 2(2m – 3).6 + 5m – 6 ≥ 0.
⇔ 36(m – 2) + 12(2m – 3) + 5m – 6 ≥ 0
⇔ 65m – 114 ≥ 0
Vậy thỏa mãn yêu cầu bài toán.
Ta chọn phương án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số bậc hai f(x) có đồ thị như hình bên.
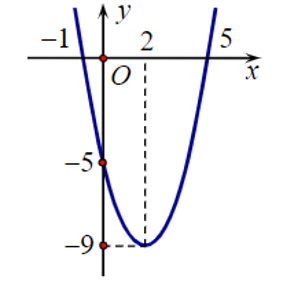
Tập nghiệm của bất phương trình f(x) ≥ 0 là:
Cho hàm số bậc hai f(x) có đồ thị như hình bên.
Tập nghiệm của bất phương trình f(x) ≥ 0 là:
Xem đáp án »
19/01/2024
59
Câu 3:
Cho f(x) = –x2 – 4x + 5. Có bao nhiêu giá trị nguyên của x thỏa mãn f(x) ≥ 0?
Cho f(x) = –x2 – 4x + 5. Có bao nhiêu giá trị nguyên của x thỏa mãn f(x) ≥ 0?
Xem đáp án »
19/01/2024
54
