Cho ∆ABC  = ∆MNP. Hai tia phân giác của góc B và C cắt nhau tại O tạo thành góc BOC bằng 120°. Tính tổng số đo các góc MNP và MPN của

Bài 26 trang 73 SBT Toán 7 Tập 2: Cho ∆ABC  = ∆MNP. Hai tia phân giác của góc B và C cắt nhau tại O tạo thành góc BOC bằng 120°. Tính tổng số đo các góc MNP và MPN của tam giác MNP.

Trả lời

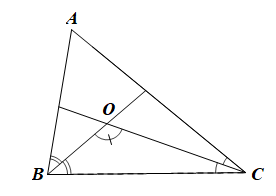
Vì BO là phân giác của góc ABC nên $\widehat{ABO}=\widehat{CBO}=\frac{\widehat{ABC}}{2}$

Vì CO là phân giác của góc ACB nên $\widehat{ACO}=\widehat{BCO}=\frac{\widehat{ACB}}{2}$

Xét $∆$COB ta có: $\widehat{BOC}+\widehat{OBC}+\widehat{OCB}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{OBC}+\widehat{OCB}=180°-\widehat{BOC}=180°-120°=60°.$

Mà $\widehat{CBO}=\frac{\widehat{ABC}}{2},\widehat{BCO}=\frac{\widehat{ACB}}{2}.$ 

Suy ra $\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}=60°$

Do đó $\widehat{ABC}+\widehat{ACB}=2.60°=120°.$

Mặt khác ∆ABC  = ∆MNP nên ta có:

$\widehat{ABC}=\widehat{MNP}$ và $\widehat{ACB}=\widehat{MPN}$(các cặp góc tương ứng).

Suy ra $\widehat{MNP}+\widehat{MPN}=\widehat{ABC}+\widehat{ACB}=120°$

Vậy $\widehat{MNP}+\widehat{MPN}=120°$.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 1. Tổng các góc của một tam giác

Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Bài 3. Hai tam giác bằng nhau

Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6. Trường hợp bằng nhau thứ ba của tam giác: