Bảng sau thống kê số ca nhiễm mới SARS – coV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam. a) Xác định số trung bình và tứ phân vị

Bài 9 trang 144 Toán 11 Tập 1: Bảng sau thống kê số ca nhiễm mới SARS – coV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam.

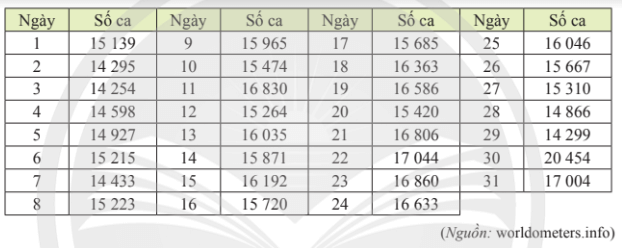
a) Xác định số trung bình và tứ phân vị của mẫu số liệu trên. Mẫu số liệu có bao nhiêu giá trị ngoại lệ?

b) Hoàn thiện bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng số trung bình và tứ phân vị của mẫu số liệu ở bảng tần số ghép nhóm trên.

Trả lời

a) Số ca nhiễm mới SARS – coV – 2 trung bình là:

$\frac{15139+14295+...+20454+17004}{31}\approx 15882$ (ca).

Dãy số liệu được sắp xếp theo chiều không giảm ta được:

14 254; 14 295; 14 299; 14 433; 14 598; 14 866; 14 927; 15 139; 15 215; 15 223; 15 264; 15 310; 15 420; 15 474; 15 667; 15 685; 15 720; 15 871; 15 965; 16 035; 16 046; 16 192; 16 363; 16 586; 16 633; 16 806; 16 830; 16 860; 17 004; 17 044; 20 454.

b) Ta có bảng tần số ghép nhóm như sau:

c) Ước lượng số ca nhiễm trung bình mỗi ngày:

$\overline{x}=\frac{14,75.14+16,25.14+17,75.2+19,25.0+20,75.1}{31}\approx 15,8$.

Gọi x₁; ...; x₃₁ là số ca nhiễm mới SARS – coV – 2 mỗi ngày theo thứ tự không giảm.

Ta có: x₁; ...; x₁₄ ∈ [14; 15,5), x₁₅; ...; x₂₈ ∈ [15,5; 17), x₂₉; x₃₀ ∈ [18,5; 20), x₃₁ ∈ [20; 21,5).

Khi đó:

Tứ phân vị thứ hai là x₁₆ ∈ [15,5; 17), nên ta có:

$Q_2=15,5+\frac{\frac{31}{2}-14}{14}.(17-15,5)=15,66$.

Tứ phân vị thứ nhất là x₈ ∈ [14; 15,5) nên ta có:

$Q_1=14+\frac{\frac{31}{4}-0}{14}.(15,5-14)=14,83$.

Tứ phân vị thứ ba x₂₃ ∈ [15,5; 17) nên ta có:

$Q_3=15,5+\frac{\frac{3.31}{4}-14}{14}.(17-15,5)=16,49$.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 4

Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm

Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

Bài tập cuối chương 5

Bài 1: Tìm hiểu hàm số lượng giác bằng phần mềm GeoGebra

Bài 2: Dùng công thức cấp số nhân để dự báo dân số