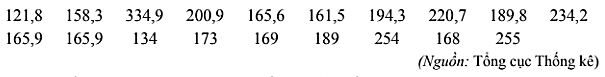Giải SGK Toán 11 (Chân trời sáng tạo): Bài tập cuối chương 5

Giải Toán 11 Bài tập cuối chương 5

Câu hỏi trắc nghiệm

Chọn phương án đúng

Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).

Bài 1 trang 143 Toán 11 Tập 1: Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?

A. [7; 9);

B. [9; 11);

C. [11; 13);

D. [13; 15).

Lời giải:

Đáp án đúng là: B

Ta có bảng giá trị đại diện sau:

Giá trị trung bình của mẫu số liệu là:

$\overline{x}=\frac{6.2+8.7+10.7+12.3+14.1}{20}=9,4$ ∈ [9; 11).

Bài 2 trang 143 Toán 11 Tập 1: Trung vị của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?

A. [7; 9);

B. [9; 11);

C. [11; 13);

D. [13; 15).

Lời giải:

Đáp án đúng là: B

Tổng số ngày là 20.

Gọi x₁; ...; x₂₀ là doanh thu của cửa hàng trong 20 ngày sắp xếp theo thứ tự không giảm.

Ta có: x₁; x₂ ∈ [5; 7), x₃; ...; x_9­ ∈ [7; 9), x₁₀; ...; x₁₆ ∈ [9; 11), x₁₇; x₁₈; x₁₉ ∈ [11; 13), x₂₀ ∈ [13; 15).

Khi đó:

Trung vị của mẫu số liệu là $\frac{1}{2}\left(x_{10}+x_{11}\right)$ và x₁₀, x₁₁ ∈ [9; 11) nên ta có:

$Q_2=9+\frac{\frac{20}{2}-9}{7}(11-9)\approx 9,3$ ∈ [9; 11).

Bài 3 trang 143 Toán 11 Tập 1: Mốt của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?

A. [7; 9);

B. [9; 11);

C. [11; 13);

D. [13; 15).

Lời giải:

Đáp án đúng là: A và B

Mốt của mẫu số liệu thuộc vào cả hai khoảng [7; 9) và [9; 11).

Bài 4 trang 143 Toán 11 Tập 1: Tứ phân vị thứ nhất của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?

A. 7;

B. 7,6;

C. 8;

D. 8,6.

Lời giải:

Đáp án đúng là: B

Tứ phân vị thứ nhất là $\frac{1}{2}\left(x_5+x_6\right)$ và x₅; x₆ ∈ [7; 9) nên ta có:

$Q_2=7+\frac{\frac{20}{4}-2}{7}(9-7)\approx 7,86$.

Vậy giá trị này sẽ gần với giá trị 7,6.

Bài 5 trang 143 Toán 11 Tập 1: Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?

A. 10;

B. 11;

C. 12;

D. 13.

Lời giải:

Đáp án đúng là: B

Tứ phân vị thứ nhất là $\frac{1}{2}\left(x_{15}+x_{16}\right)$ và x₁₅; x₁₆ ∈ [9; 11) nên ta có:

$Q_2=9+\frac{\frac{3.20}{4}-9}{7}.(11-9)\approx 10,71$.

Vậy giá trị này sẽ gần với giá trị 11.

Bài tập tự luận

Bài 6 trang 143 Toán 11 Tập 1: Thống kê điểm trung bình môn Toán của một số học sinh lớp 11 được cho ở bảng sau:

Hãy uớc lượng số trung bình, tứ phân vị và mốt của mẫu số liệu ghép nhóm trên.

Lời giải:

Ta có bảng giá trị đại diện:

+) Ước lượng trung bình của mẫu số liệu là:

$\frac{6,75.8+7,25.10+7,75.16+8,25.24+8,75.13+9,25.7+9,75.4}{82}\approx 8,12$.

+) Gọi x₁; ...; x₈₂ là điểm trung bình môn Toán của một số học sinh lớp 11 được sắp xếp theo chiều ko giảm.

Ta có: x₁; ...; x₈ ∈ [6,5; 7), x₉; ...; x₁₈ ∈ [7; 7,5), x₁₉; ...; x₃₄ ∈ [7,5; 8), x₃₅; ...; x₅₈ ∈ [8; 8,5), x₅₉; ...; x₇₁ ∈ [8,5; 9), x₇₂; ...; x₇₈ ∈ [9; 9,5), x₇₉; ...; x₈₂ ∈ [9,5; 10).

Trung vị của mẫu số liệu là $\frac{1}{2}\left(x_{41}+x_{42}\right)$ và x₄₁; x₄₂ ∈ [8; 8,5) nên ta có:

$Q_2=8+\frac{\frac{82}{2}-34}{24}.(8,5-8)\approx 8,15$.

+) Mốt của mẫu số liệu thuộc khoảng [8; 8,5) nên:

$M_0=8+\frac{24-16}{24-16+24-13}.(8,5-8)\approx 8,21$.

Bài 7 trang 143 Toán 11 Tập 1: Để kiểm tra thời gian sử dụng pin của chiếc điện thoại mới, chị An thống kê thời gian sử dụng điện thoại của mình từ lúc sạc đầy pin cho đến khi hết pin ở bảng sau:

a) Hãy ước lượng thời gian sử dụng trung bình từ lúc chị An sạc đầy pin điện thoại cho tới khi hết pin.

b) Chị An cho rằng có khoảng 25% số lần sạc điện thoại chỉ dùng được dưới 10 giờ. Nhận định của chị An có hợp lí không?

Lời giải:

Ta có bảng giá trị đại diện:

a) Thời gian sử dụng trung bình từ lúc c An sạc đầy điện thoại cho đến khi hết pin là:

$\overline{x}=\frac{8.2+10.5+12.7+14.6+16.3}{23}\approx 12,26$.

b) Tổng số lần sử dụng là: 2 + 5 + 7 + 6 + 3 = 23 (lần).

Gọi x₁; ...; x₂₃ là thời gian sử dụng của pin điện thoại mới sau mỗi lần theo thứ tự không giảm.

Ta có: x₁; x₂ ∈ [7; 9), x₃; ...; x₇ ∈ [9; 11), x₈; ...; x₁₄ ∈ [11; 13), x₁₅; ...; x₂₀ ∈ [13; 15), x₂₁; x₂₂; x₂₃ ∈ [15; 17).

Tứ phân vị thứ nhất là x₆ ∈ [9; 11) nên ta có: $Q_1=9+\frac{\frac{23}{4}-2}{5}.(11-9)=10,5$.

Bài 8 trang 144 Toán 11 Tập 1: Tổng lượng mưa trong tháng 8 đo được tại một trạm quan trắc đặt tại Vũng Tàu từ năm 2002 đến năm 2020 được ghi lại như dưới đây (đơn vị: mm):

a) Xác định số trung bình, tứ phân vị và mốt của mẫu số liệu trên.

b) Hoàn thiện bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng số trung bình, tứ phân vị và mốt của mẫu số liệu ở bảng tần số ghép nhóm trên.

Lời giải:

a) Mẫu số liệu được sắp xếp theo thứ tự không giảm ta được:

121,8; 134; 158,3; 161,5; 165,6; 165,9; 165,9; 168; 169; 173; 189; 189,8; 194,3; 200,9; 220,7; 234,2; 254; 255; 334,9.

Tổng số năm điều tra là 19 năm.

Lượng mưa trung bình qua 19 năm tại Vũng Tàu là:

$\overline{x}=\frac{121,8+134+...+165,6+165,9+165,9+...+255+334,9}{19}\approx 192,4$

+) Trung vị của mẫu số liệu là giá trị thứ 10 là Q₂ = 173.

Tứ phân vị thứ nhất của nửa số liệu bên trái là giá trị thứ 5 là Q₁ = 165,6.

Tứ phân vị thứ ba của nửa số liệu bên phải là giá trị thứ 15 là Q₃ = 220,7.

+) Mốt của mẫu số liệu là M₀ = 165,9.

b) Ta có bảng tần số ghép nhóm như sau:

c) Ước lượng giá trị trung bình dựa vào bảng giá tần số ghép nhóm ta được:

$\overline{x}=\frac{147,5.10+202,5.5+257,5.3+312,5}{19}\approx 188,03$

+) Gọi x₁; ...; x₁₉ là lượng mua trung bình ở Vũng Tàu qua các năm theo thứ tự không giảm.

Ta có: x₁; ...; x₁₀ ∈ [120; 175), x₁₁; ...; x₁₅ ∈ [175; 230), x₁₆; ...; x₁₈ ∈ [230; 285), x₁₉ ∈ [285; 340).

Tứ phân vị thứ hai là x₁₀ ∈ [120; 175) nên ta có:

$Q_2=120+\frac{\frac{19}{2}}{10}.(175-120)=172,25$.

Tứ phân vị thứ nhất là x₅ ∈ [120; 175) nên ta có:

$Q_1=120+\frac{\frac{19}{4}}{10}.(175-120)=146,125$.

Tứ phân vị thứ ba là x₁₅ ∈ [175; 230) nên ta có:

$Q_3=175+\frac{\frac{3.19}{4}-10}{5}.(230-175)=221,75$.

+) Mốt của mẫu số liệu thuộc [120; 175) nên ta có:

$M_0=120+\frac{10}{10+10-5}.(175-120)\approx 156,7$.

Bài 9 trang 144 Toán 11 Tập 1: Bảng sau thống kê số ca nhiễm mới SARS – coV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam.

a) Xác định số trung bình và tứ phân vị của mẫu số liệu trên. Mẫu số liệu có bao nhiêu giá trị ngoại lệ?

b) Hoàn thiện bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng số trung bình và tứ phân vị của mẫu số liệu ở bảng tần số ghép nhóm trên.

Lời giải:

a) Số ca nhiễm mới SARS – coV – 2 trung bình là:

$\frac{15139+14295+...+20454+17004}{31}\approx 15882$ (ca).

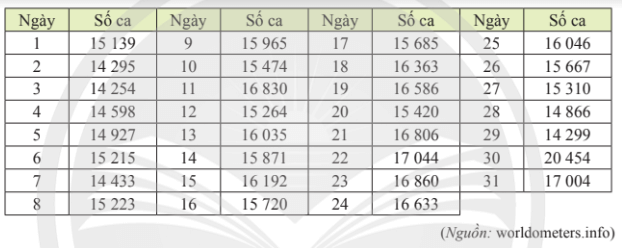
Dãy số liệu được sắp xếp theo chiều không giảm ta được:

14 254; 14 295; 14 299; 14 433; 14 598; 14 866; 14 927; 15 139; 15 215; 15 223; 15 264; 15 310; 15 420; 15 474; 15 667; 15 685; 15 720; 15 871; 15 965; 16 035; 16 046; 16 192; 16 363; 16 586; 16 633; 16 806; 16 830; 16 860; 17 004; 17 044; 20 454.

b) Ta có bảng tần số ghép nhóm như sau:

c) Ước lượng số ca nhiễm trung bình mỗi ngày:

$\overline{x}=\frac{14,75.14+16,25.14+17,75.2+19,25.0+20,75.1}{31}\approx 15,8$.

Gọi x₁; ...; x₃₁ là số ca nhiễm mới SARS – coV – 2 mỗi ngày theo thứ tự không giảm.

Ta có: x₁; ...; x₁₄ ∈ [14; 15,5), x₁₅; ...; x₂₈ ∈ [15,5; 17), x₂₉; x₃₀ ∈ [18,5; 20), x₃₁ ∈ [20; 21,5).

Khi đó:

Tứ phân vị thứ hai là x₁₆ ∈ [15,5; 17), nên ta có:

$Q_2=15,5+\frac{\frac{31}{2}-14}{14}.(17-15,5)=15,66$.

Tứ phân vị thứ nhất là x₈ ∈ [14; 15,5) nên ta có:

$Q_1=14+\frac{\frac{31}{4}-0}{14}.(15,5-14)=14,83$.

Tứ phân vị thứ ba x₂₃ ∈ [15,5; 17) nên ta có:

$Q_3=15,5+\frac{\frac{3.31}{4}-14}{14}.(17-15,5)=16,49$.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 4

Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm

Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

Bài 1: Tìm hiểu hàm số lượng giác bằng phần mềm GeoGebra

Bài 2: Dùng công thức cấp số nhân để dự báo dân số