Cho hình bình hành ABCD có AB = 4, AD = 6, góc BAD = 60độ (Hình 74). a) Biểu thị các vectơ BD, vectơ AC theo vectơ AB, vectơ AD

Bài 8 trang 100 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có AB = 4, AD = 6, $\widehat{BAD}=60°$ (Hình 74).

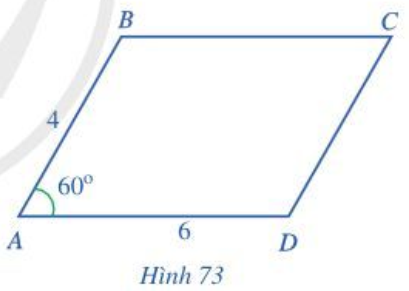
a) Biểu thị các vectơ $\overrightarrow{BD},\overrightarrow{AC}$ theo $\overrightarrow{AB},\overrightarrow{AD}$.

b) Tính các tích vô hướng $\overrightarrow{AB}.\overrightarrow{AD},\overrightarrow{AB}.\overrightarrow{AC},\overrightarrow{BD}.\overrightarrow{AC}$.

c) Tính độ dài các đường chéo BD, AC.

Trả lời

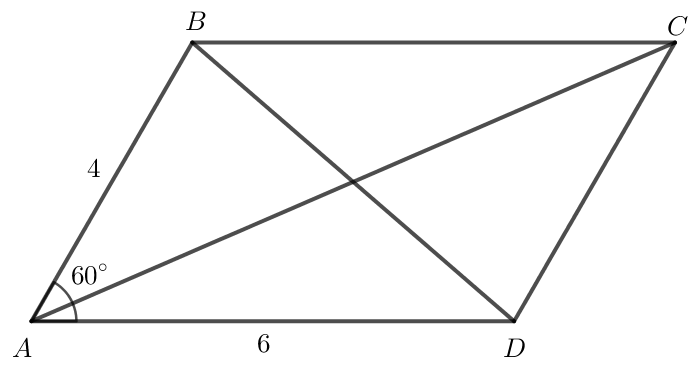
a) Ta có $\overrightarrow{B\text{D}}=\overrightarrow{AD}-\overrightarrow{AB}$.

Áp dụng quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.

b) Ta có $\overrightarrow{AB}.\overrightarrow{AD}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AD}\right|.\cos \left(\overrightarrow{AB},\overrightarrow{AD}\right)$

= 4 . 6 . cos $\widehat{BAD}$ = 24 . cos 60^o = 12.

$\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{AB}.\left(\overrightarrow{AB}+\overrightarrow{AD}\right)={\overrightarrow{AB}}^2+\overrightarrow{AB}.\overrightarrow{AD}$ = 4² + 12  = 28.

$$\begin{gathered} \overrightarrow{BD}.\overrightarrow{AC}=\left(\overrightarrow{AD}-\overrightarrow{AB}\right).\left(\overrightarrow{AB}+\overrightarrow{AD}\right) \\ =\overrightarrow{AD}.\overrightarrow{AB}+{\overrightarrow{AD}}^2-{\overrightarrow{AB}}^2-\overrightarrow{AB}.\overrightarrow{AD} \end{gathered}$$ 

= 6² - 4² = 20.

c) Áp dụng định lí côsin vào tam giác ABD có:

BD² = AB² + AD² - 2.AB.AD.cos $\widehat{BAD}$

$\Rightarrow$ BD² = 4² + 6² - 2.4.6.cos 60^o

$\Rightarrow$ BD² = 28

$\Rightarrow$ BD = $2\sqrt{7}$

Do ABCD là hình bình hành nên $\widehat{BA\text{D}}+\widehat{ADC}=180°$.

Do đó $\widehat{A\text{D}C}=180°-\widehat{BA\text{D}}=180°-60°=120°$.

Áp dụng định lí côsin vào tam giác ADC có:

CD² = AD² + DC² - 2.AD.DC.cos $\widehat{ADC}$

$\Rightarrow$ CD² = 6² + 4² - 2.6.4.cos 120^o

$\Rightarrow$ CD² = 76

$\Rightarrow$ CD = $2\sqrt{19}$

Vậy BD = $2\sqrt{7}$; CD = $2\sqrt{19}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài 5: Tích của một số với một vectơ

Bài 6: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Chủ đề 1: Đo góc

Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây

Bài 2: Hoán vị. Chỉnh hợp