Chứng minh: a) Nếu ABCD là hình bình hành thì vectơ AB + vectơ AD + vectơ CE = vectơ AE với E là điểm bất kì
812
10/06/2023
Bài 7 trang 100 Toán lớp 10 Tập 1: Chứng minh:
a) Nếu ABCD là hình bình hành thì →AB+→AD+→CE=→AE với E là điểm bất kì;
b) Nếu I là trung điểm của đoạn thẳng AB thì →MA+→MB+2→IN=2→MN với M, N là hai điểm bất kì;
c) Nếu G là trọng tâm của tam giác ABC thì →MA+→MB+→MC−3→MN=3→NG với M, N là hai điểm bất kì.
Trả lời
a)
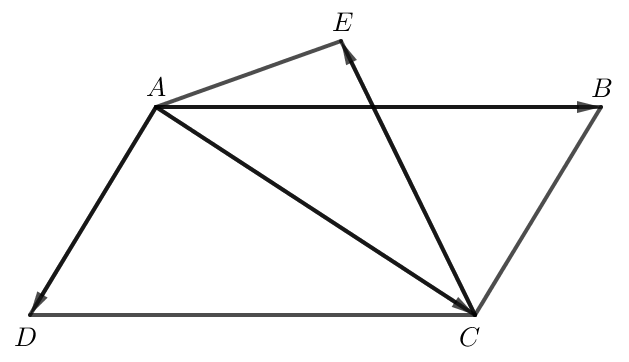
Áp dụng quy tắc hình bình hành ta có →AB+→AD=→AC.
Do đó →AB+→AD+→CE=→AC+→CE=→AE.
Vậy →AB+→AD+→CE=→AE.
b)
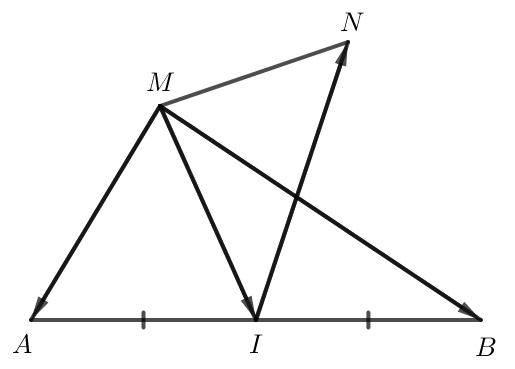
Do I là trung điểm của AB nên →MA+→MB=2→MI.
Do đó →MA+→MB+2→IN=2→MI+2→IN=2(→MI+→IN)=2→MN.
Vậy →MA+→MB+2→IN=2→MN.
c)
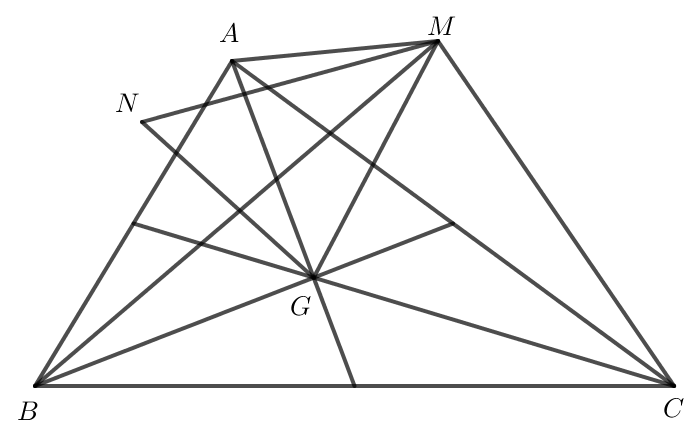
Do G là trọng tâm của tam giác ABC nên →MA+→MB+→MC=3→MG.
Do đó →MA+→MB+→MC−3→MN=3→MG−3→MN=3(→MG−→MN)=3→NG.
Vậy →MA+→MB+→MC−3→MN=3→NG.
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 5: Tích của một số với một vectơ
Bài 6: Tích vô hướng của hai vectơ
Bài tập cuối chương 4
Chủ đề 1: Đo góc
Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây
Bài 2: Hoán vị. Chỉnh hợp



