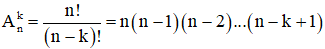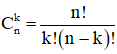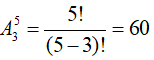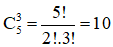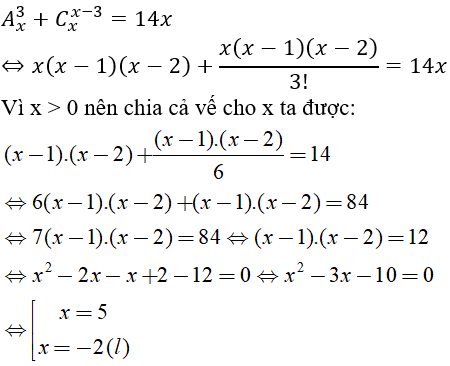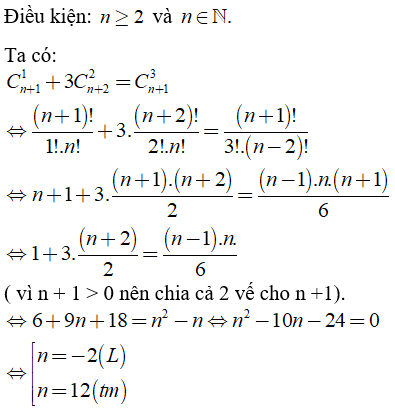Cách tính tổ hợp chập K của N phần tử
I. Phương pháp giải
Cho tập hợp A có n phần tử và cho số nguyên k, (1 ≤ k ≤ n). Mỗi tập hợp con của A có k phần tử được gọi là một tổ hợp chập k của n phần tử của A.
- Số các tổ hợp chập k của một tập hợp có n phần tử là : Ckn= .
- Tính chất :
- Đặc điểm: Tổ hợp là chọn phần tử không quan trọng thứ tự, số phần tử được chọn là k: 0 ≤ k ≤ n
II. Bài tập vận dụng
Bài 1: Một tổ gồm 12 học sinh. Có bao nhiêu cách:
a) Chọn ra 2 bạn đại diện cho nhóm
b) Chọn ra 2 bạn, rồi phân công chứ vụ tổ trưởng và tổ phó
c) Chia tổ thành 2 nhóm, trong đó tổ trưởng và tổ phó khác nhóm.
Lời giải
a) Chọn 2 bạn từ 12 bạn là tổ hợp chập 2 của 12: C122 = 66 cách.
b) Chọn 2 bạn rồi phân công chức vị là chỉnh hợp chập 2 của 12: A122 = 132 cách.
c) Chia tổ thành 2 nhóm tức mỗi nhóm có 6 bạn
Trong đó tổ trưởng và tổ phó khác nhóm
Chọn 5 bạn vào cùng nhóm với tổ trưởng trong 10 bạn còn lại: C105 = 252 cách.
Chọn 5 bạn vào cùng nhóm với tổ phó trong 5 bạn còn lại: C55 = 1 cách.
Vậy có 252.1 = 252 cách.
Bài 2: Một hộp có 15 viên bi đỏ và 5 viên bi xanh, 10 viên bi vàng. Có bao nhiêu cách chọn ra 5 viên sao cho
a) Các viên bi cùng màu
b) Số bi xanh bằng số bi đỏ, biết luôn có bi xanh và đỏ
c) Có ít nhất 1 viên bi xanh.
Lời giải
a) Chọn 5 viên bi cùng màu
+ Trường hợp 1: Chọn được 5 viên bi màu đỏ: có C155 = 3003 cách.
+ Trường hợp 2: Chọn được 5 viên bi màu xanh: có C55 = 1 cách.
+ Trường hợp 3: Chọn được 5 viên bi màu xanh: có C105 = 252 cách.
Vậy có 3003 + 1 + 252 = 3256 cách chọn.
b) Chọn được 5 viên bi trong đó số bi xanh bằng số bi đỏ
+ Trường hợp 1: có 1 viên bi xanh, 1 viên bi đỏ, 3 viên bi vàng: C51 . C151. C103 = 9000 cách.
+ Trường hợp 2: có 2 viên bi xanh, 2 viên bi đỏ, 1 viên bi vàng: C52 . C152. C101 = 10500 cách.
Vậy có 9000 + 10500 = 19500 cách chọn.
c) Chọn được ít nhất 1 viên bi xanh
Số cách chọn 5 viên bi bất kì là: C305 = 14250 cách.
Số cách chọn 5 viên trong đó không có bi xanh là: C255 = 53130 cách.
Vậy số cách chọn được ít nhất 1 viên bi xanh là: 142506 – 53130 = 89376 cách chọn.
Bài 3.Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
+ Số chỉnh hợp chập k của n phần tử:
+ Số tổ hợp chập k của n phần tử:
+ Ví dụ:
- Số chỉnh hợp chập 3 của 5: 
- Số tổ hợp chập 3 của 5: 
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau để cắm vào 5 lọ khác nhau:
⇒ Có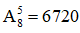 
cách chọn.
- Chọn ngẫu nhiên 5 bông hoa trong số 8 bông hoa khác nhau
⇒ Có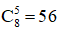 
cách chọn.
Bài 4: Giải phương trình Ax3+=14x (x là ẩn số)
Điều kiện x ∈ N và x ≥ 3, ta có:
Bài 5: Một túi đựng 6 bi trắng, 5 bi xanh. Lấy ra 4 viên bi từ túi đó. Hỏi có bao nhiêu cách lấy mà 4 viên bi lấy ra có đủ hai màu.
Lời giải:
Các viên bi lấy ra có đủ cả 2 màu nên ta có các trường hợp:
Cách 2. Dùng phần bù. Số cách chọn 4 viên bi tùy ý từ 11 viên bi là: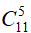 
cách.
Số cách chọn 4 viên bi màu trắng là: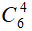 
cách.
Số cách chọn 4 viên bi là màu xanh là: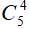 
cách.
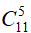
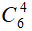
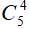
Vậy có - ( + ) = 310 cách chọn 4 viên bi trong đó có cả 2 màu.
Bài 6: Từ 20 người cần chọn ra một đoàn đại biểu gồm 1 trưởng đoàn, 1 phó đoàn, 1 thư kí và 3 ủy viên. Hỏi có bao nhiêu cách chọn đoàn đại biểu ?
Lời giải:
Bài 7: Một nhóm đoàn viên thanh niên tình nguyện về sinh hoạt tại một xã nông thôn gồm có 21 đoàn viên nam và 15 đoàn viên nữ. Hỏi có bao nhiêu cách phân chia 3 nhóm về 3 ấp để hoạt động sao cho mỗi ấp có 7 đoàn viên nam và 5 đoàn viên nữ?
Lời giải:
Nhóm thứ 1: chọn 7 nam từ 21 bạn nam, chọn 5 nữ từ 15 bạn nữ nên số cách chọn nhóm thứ nhất là: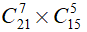 
cách.
Nhóm thứ 2: chọn 7 nam từ 14 bạn nam còn lại, chọn 5 nữ từ 10 bạn nữ còn lại nên số cách chọn nhóm thứ hai là: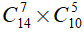 
cách.
Số cách chọn nhóm thứ ba là: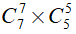 
cách.
Vậy có 
cách chia nhóm.
Bài 8: Có 12 học sinh giỏi gồm 3 học sinh khối 12, 4 học sinh khối 11 và 5 học sinh khối 10. Hỏi có bao nhiêu cách chọn ra 6 học sinh trong số học sinh giỏi đó sao cho mỗi khối có ít nhất 1 học sinh?
Lời giải:
Số cách chọn 6 học sinh bất kì trong 12 học sinh là: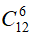 
cách.
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 10 ( hay 6 học sinh từ khối 11 và 12) là: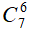 
cách.
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 11 (hay 6 học sinh từ khối 10 và 12) là: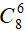 
cách.
Số cách chọn 6 học sinh mà trong đó không có học sinh khối 12 (hay 6 học sinh từ khối 10 và 11) là: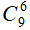 
cách.
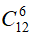
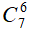
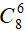
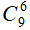
Vậy có - ( + + ) = 805 cách chọn thỏa mãn yêu cầu bài toán.
Bài 9: Một hộp bi có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Hỏi có bao nhiêu cách lấy ra 4 viên bi trong đó số viên bi đỏ lớn hơn số viên bi vàng.
Tổng số bi lấy ra có 4 viên mà bi đỏ nhiều hơn bi vàng nên có 2 trường hợp xảy ra:
TH1: Không có bi vàng, khi đó số bi đỏ phải từ 1 viên trở lên.
Số cách lấy 4 viên bi bất kì trong tổng số 9 viên bi (gồm 5 đỏ và 4 xanh) là: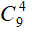 
cách.
Số cách lấy 4 viên bi xanh ( khi đó bi đỏ không được lấy ra) là: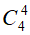 
cách.
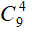
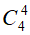
Số cách lấy thỏa mãn trong trường hợp này là: - = 125 cách.
TH2: Có 1 viên bi vàng, khi đó số bi đỏ phải từ 2 viên trở lên.
Số cách lấy 1 viên bi vàng: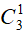 
cách.
Số cách lấy 3 viên bi còn lại trong đó có 2 bi đỏ và 1 bi xanh là: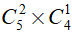 
cách.
Số cách lấy 3 viên bi còn lại đều là bi đỏ là: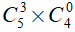 
cách.
Số cách lấy thỏa mãn trong trường hợp này là:
* ( + ) = 150 cách.
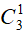
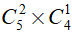
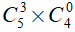
Vậy có 125 + 150 = 275 cách lấy thỏa mãn yêu cầu bài toán.
Bài 10: Tìm giá trị n ∈ N thỏa mãn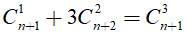 
.
Lời giải:
Bài 11: Cho 10 điểm phân biệt A1, A2, ..., A10 trong đó có 4 điểm A1, A2, A3, A4 thẳng hàng, ngoài ra không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác có 3 đỉnh được lấy trong 10 điểm trên?
Lời giải:
Số cách lấy 3 điểm từ 10 điểm phân biệt là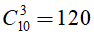 
.
Số cách lấy 3 điểm bất kì trong 4 điểm A1, A2, A3, A4 là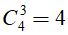 
.
Khi lấy 3 điểm bất kì trong 4 điểm A1, A2, A3, A4 thì sẽ không tạo thành tam giác.
Như vậy, số tam giác tạo thành : 120 - 4 = 116 tam giác.
Bài 12: Cho hai đường thẳng song song d1 và d2. Trên d1 lấy 17 điểm phân biệt, trên d2 lấy 20 điểm phân biệt. Tính số tam giác mà có các đỉnh được chọn từ 37 điểm này.
Lời giải:
Một tam giác được tạo bởi ba điểm phân biệt nên ta xét:
TH1. Chọn 1 điểm thuộc d1 và 2 điểm thuộc d2: có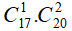 
tam giác.
TH2. Chọn 2 điểm thuộc d1 và 1 điểm thuộc d2: có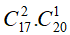 
tam giác.
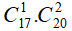
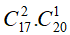
Như vậy, ta có + = 5950 tam giác cần tìm.
Xem thêm các dạng bài tập hay, có đáp án:
