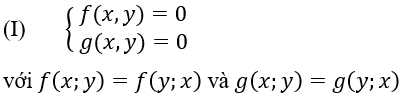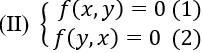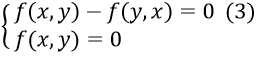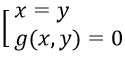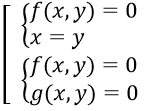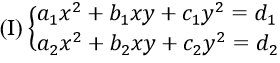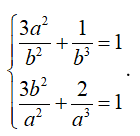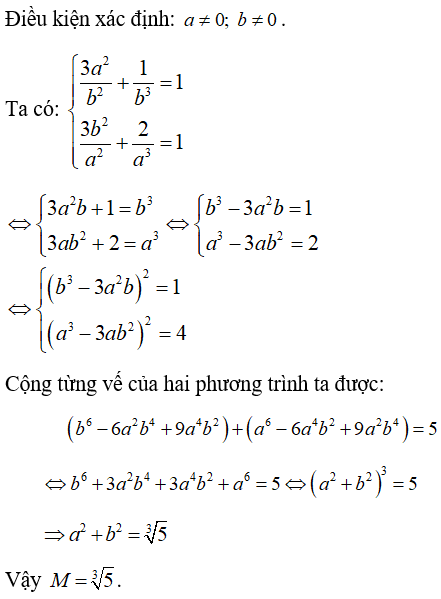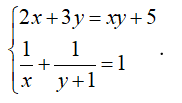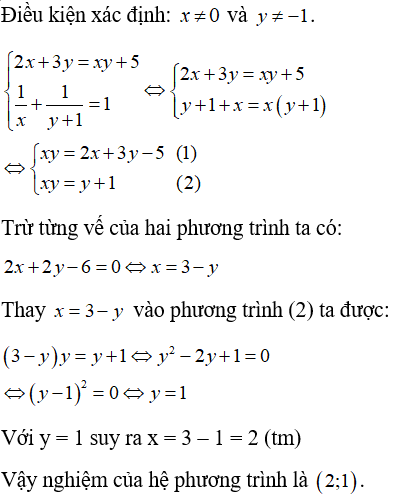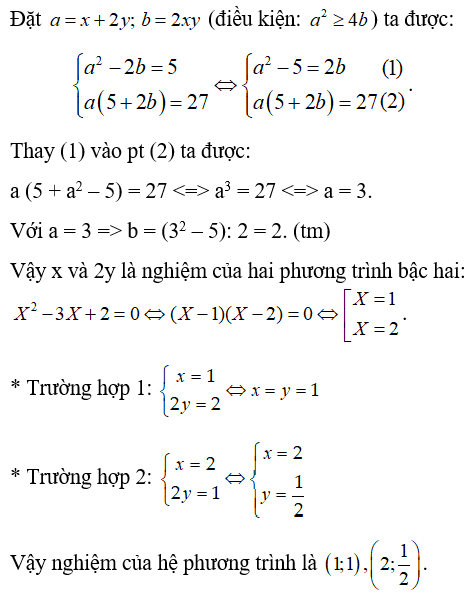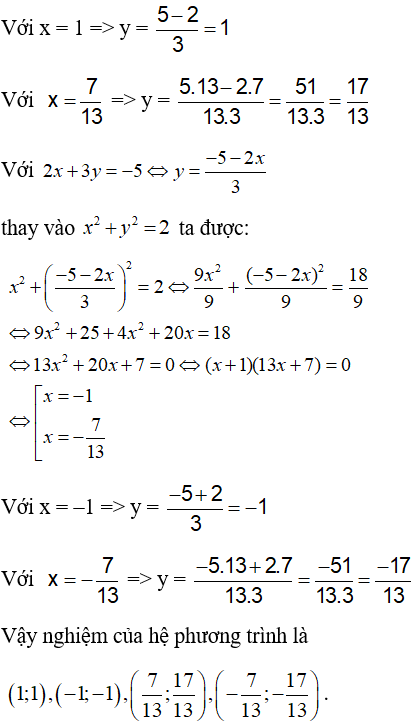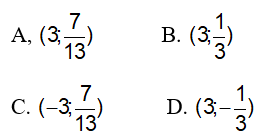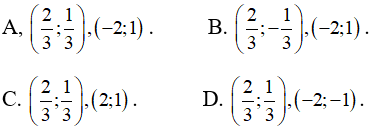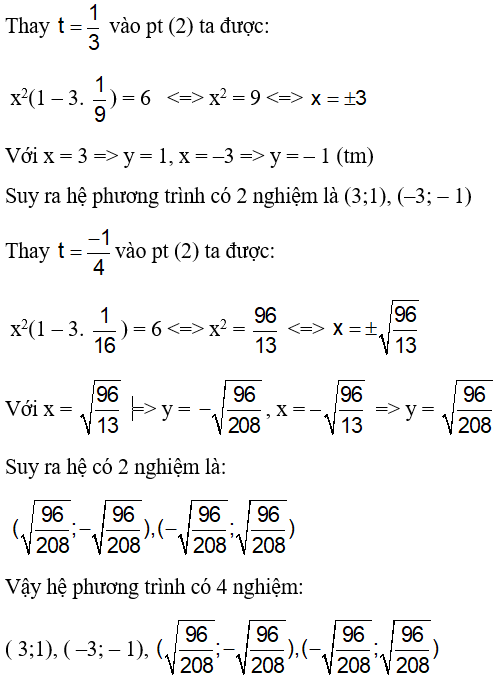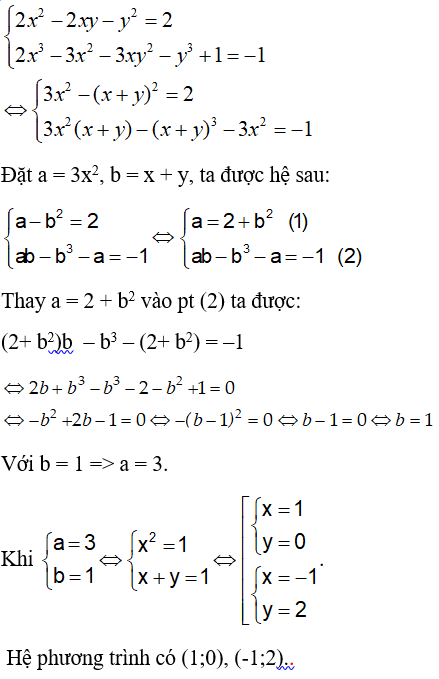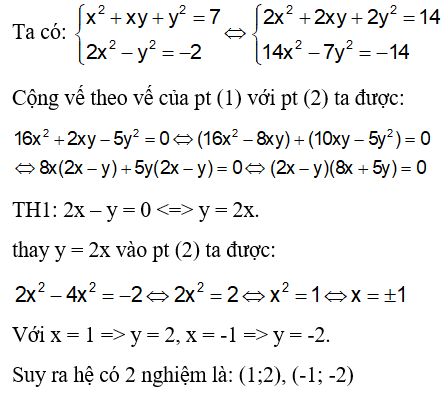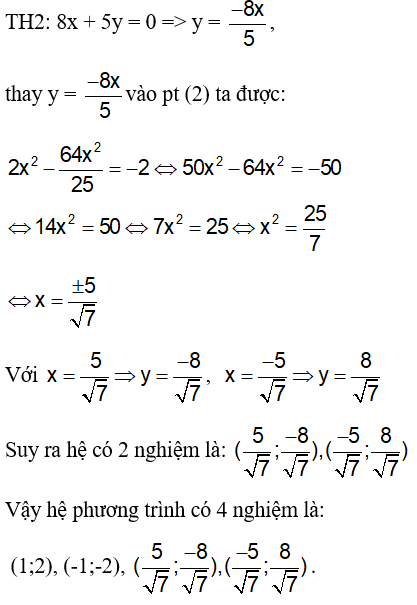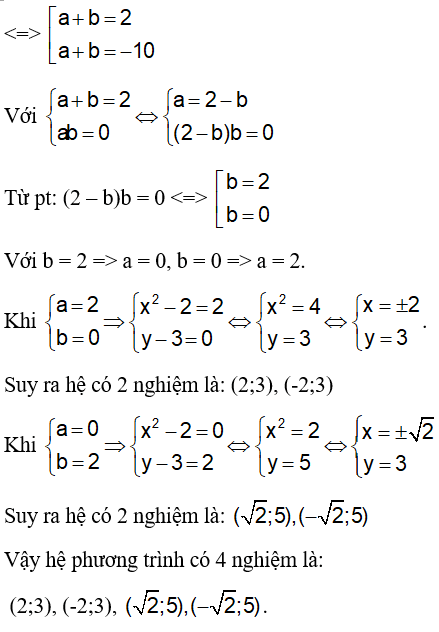Cách giải hệ phương trình đặc biệt, nâng cao cực hay
Phương pháp giải
DẠNG TOÁN 1: HỆ GỒM MỘT PHƯƠNG TRÌNH BẬC NHẤT VÀ MỘT BẬC HAI
1. Phương pháp giải
Sử dụng phương pháp thế
- Từ phương trình bậc nhất rút một ẩn theo ẩn kia.
- Thế vào phương trình bậc hai để đưa về phương trình bậc hai một ẩn.
- Số nghiệm của hệ tuỳ theo số nghiệm của phương trình bậc hai này.
DẠNG TOÁN 2: HỆ PHƯƠNG TRÌNH ĐỐI XỨNG
1. Phương pháp giải
a. Hệ đối xứng loại 1
Hệ phương trình đối xứng loại 1 là hệ phương trình có dạng:
(Có nghĩa là khi ta hoán vị giữa x và y thì f(x, y) và g(x, y) không thay đổi).
Cách giải
- Đặt S = x + y, P = xy
- Đưa hệ phương trình (I) về hệ (I') với các ẩn là S và P.
- Giải hệ (I') ta tìm được S và P
- Tìm nghiệm (x; y) bằng cách giải phương trình: X2 - SX + P = 0
b. Hệ đối xứng loại 2
Hệ phương trình đối xứng loại 2 là hệ phương trình có dạng:
(Có nghĩa là khi hoán vị giữa x và y thì (1) biến thành (2) và ngược lại)
- Trừ (1) và (2) vế theo vế ta được: (II) ⇔ 
- Biến đổi (3) về phương trình tích: (3) ⇔ (x-y).g(x,y) = 0 ⇔ 
- Như vậy (II) ⇔ 
- Giải các hệ phương trình trên ta tìm được nghiệm của hệ (II)
c. Chú ý
Hệ phương trình đối xứng loại 1, 2 nếu có nghiệm là (x0; y0) thì (y0; x0) cũng là một nghiệm của nó
DẠNG TOÁN 3: HỆ PHƯƠNG TRÌNH ĐẲNG CẤP BẬC HAI
1. Phương pháp giải
Hệ phương trình đẳng cấp bậc hai là hệ phương trình có dạng:
- Giải hệ khi x = 0 (hoặc y = 0)
- Khi x ≠ 0, đặt y = tx. Thế vào hệ (I) ta được hệ theo k và x. Khử x ta tìm được phương trình bậc hai theo k. Giải phương trình này ta tìm được k, từ đó tìm được (x; y)
Ví dụ minh họa
Ví dụ 1: Cho hệ phương trình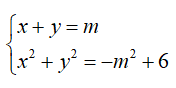 
(m là tham số). Hãy tìm các giá trị của m để hệ phương trình có nghiệm (x,y) sao cho biểu thức A = xy + 2(X+y) đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Hướng dẫn giải:
Ví dụ 2: : Tính giá trị của biểu thức M = a2+b2 biết a, b thỏa mãn: 
Hướng dẫn giải:
Ví dụ 3: Giải hệ phương trình 
Hướng dẫn giải:
Bài tập trắc nghiệm (có đáp án)
Câu 1: Cho hệ phương trình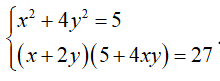 
. Hệ có bao nhiêu nghiệm nguyên?
A. 1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: A
Ta có:
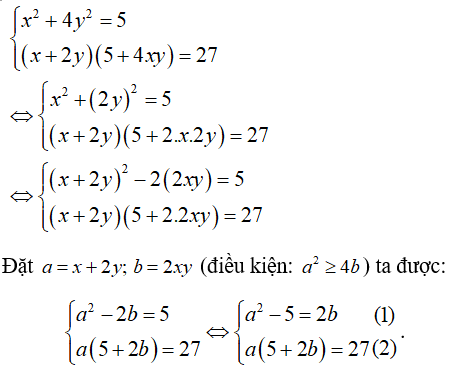
Câu 2: Giải hệ phương trình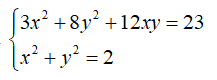 
có bao nhiêu nghiệm là?
A. 1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: D
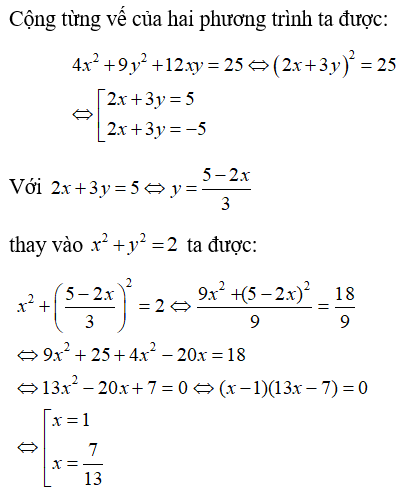
Câu 3: Cho hệ phương trình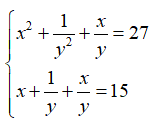 
. Nghiệm của hệ phương trình là:
Lời giải:
Đáp án: B
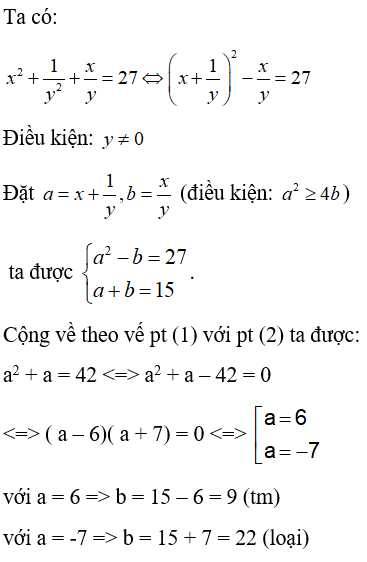
Câu 4: Cho hệ phương trình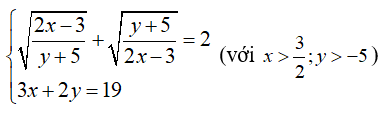 
. Tính x + y = ?
A. 5 B.6 C.7 D.8
Lời giải:
Đáp án: C
Vậy nghiệm của hệ phương trình là (5;2). Do đó x + y = 7.
Câu 5: Cho hệ phương trình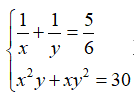 
hệ phương trình có bao nhiêu nghiệm nguyên là?
A. 1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: D
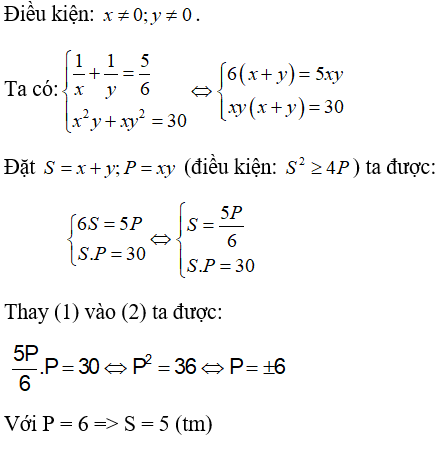
Câu 6: Cho hệ phương trình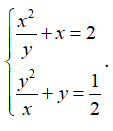 
. Nghiệm của hệ phương trình là?
Lời giải:
Đáp án: A
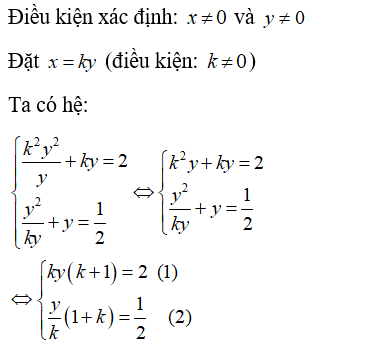
Câu 7: Cho hệ phương trình sau: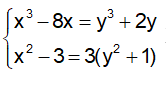
khẳng định nào sau đây đúng?
A. Hệ phương trình có một nghiệm
B. Hệ phương trình hai nghiệm
C. Hệ phượng trình có ba nghiệm
D. Hệ phương trình có bốn nghiệm
Lời giải:
Đáp án: D
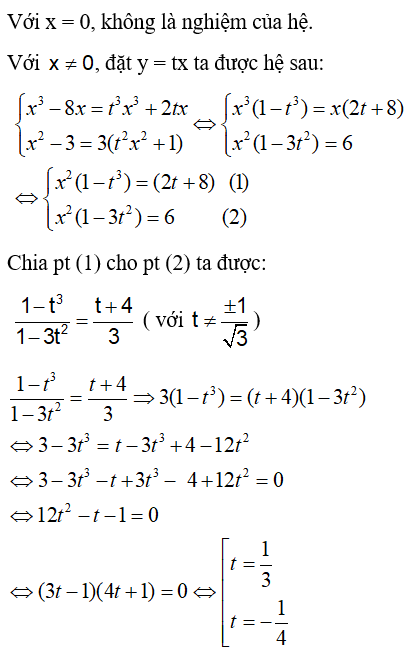
Câu 8: Cho hệ phương trình: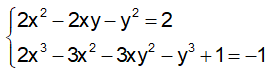
hệ có nghiệm là?
A, (-1;0), (-1;2) B. (1;0), (-1;2)
C. (-1;2), (-1;0) D. (0;2), (1;2)
Lời giải:
Đáp án: B
Câu 9: Cho hệ phương trình sau: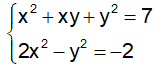
hệ có bao nhiêu nghiệm nguyên?
A. 1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: B
Câu 10: Cho hệ phương trình: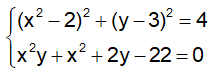 
.hệ có bao nhiêu nghiệm?
A. 1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: D
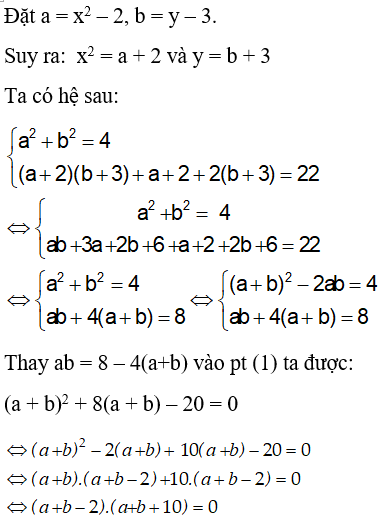
Xem thêm các dạng bài tập Toán chi tiết và hay khác:
50 Bài tập Giải hệ phương trình bằng phương pháp thế (có đáp án năm 2023)
50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2023)
50 Bài tập Phương trình bậc hai một ẩn (có đáp án năm 2023)
50 Bài tập Công thức nghiệm thu gọn (có đáp án năm 2023)
50 Bài tập Hệ thức Vi – ét và ứng dụng (có đáp án năm 2023)
