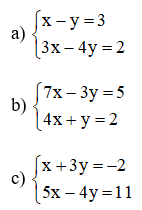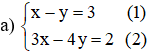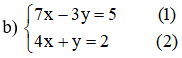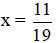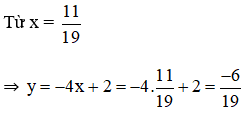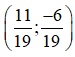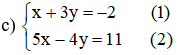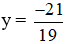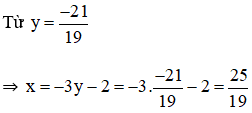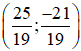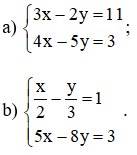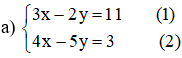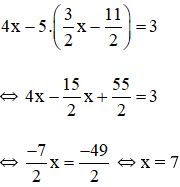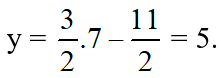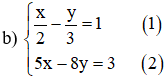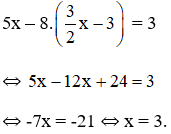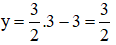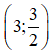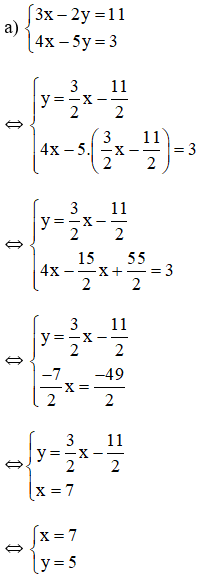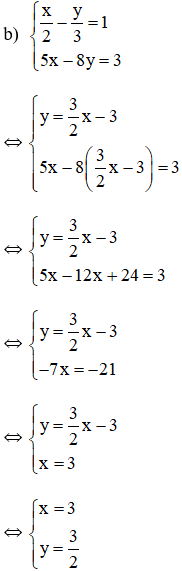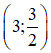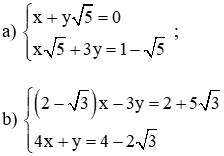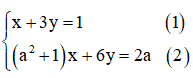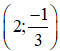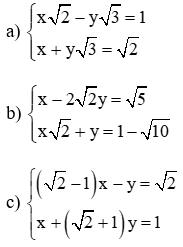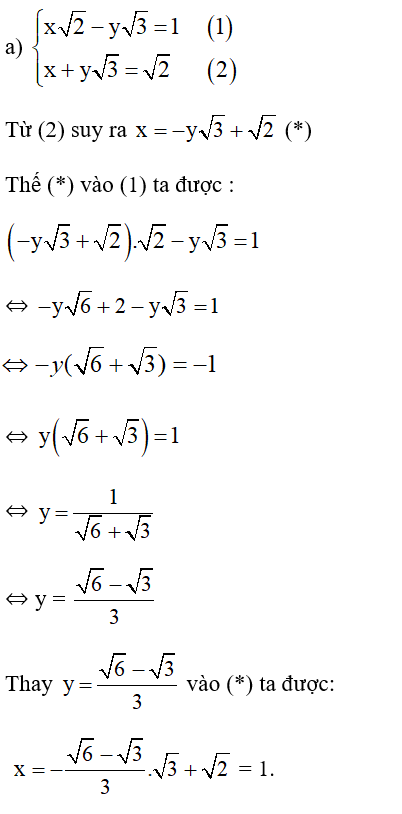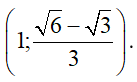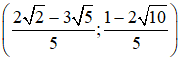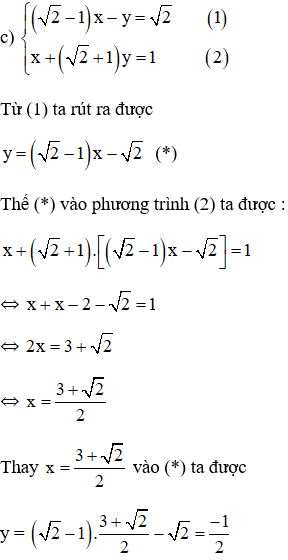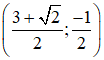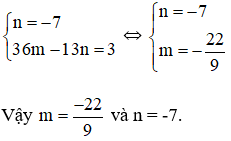50 Bài tập Giải hệ phương trình bằng phương pháp thế (có đáp án năm 2024) - Toán 9

Giải hệ phương trình bằng phương pháp thế

Kiến thức cần nhớ 

1. Quy tắc thế

Định nghĩa: Quy tắc thế dùng để biến đổi một hệ phương trình thành hệ phương trình tương đương.

Quy tắc thế gồm 2 bước sau:

Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thứ nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).

Bước 2: Dùng phương trình mới ấy để thay thế cho phương trình thứ hai trong hệ (Phương trình thứ nhất thường được thay thế bởi hệ thức biểu diễn một ẩn theo ẩn kia có được ở bước 1).

Ví dụ 1: Xét hệ phương trình: $\left\{\begin{array}{l}\mathrm{x}-2\mathrm{y}=5\\ 2\mathrm{x}+3\mathrm{y}=6\end{array}\right.$(I)

Ta thực hiện các bước rút thế như sau:

$\left\{\begin{array}{l}\mathrm{x}-2\mathrm{y}=5 \left(1\right)\\ 2\mathrm{x}+3\mathrm{y}=6 \left(2\right)\end{array}\right.$

Từ phương trình (1) ta rút được x = 2y + 5 thế vào phương trình (2) ta được:

$$\begin{gathered} \left\{\begin{array}{l}\mathrm{x}-2\mathrm{y}=5\\ 2\left(2\mathrm{y}+5\right)+3\mathrm{y}=6\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2\mathrm{y}+5\\ 4\mathrm{y}+10+3\mathrm{y}=6\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2\mathrm{y}+5\\ 7\mathrm{y}+10=6\end{array}\right. \end{gathered}$$

2. Giải hệ phương trình bằng phương pháp thế

Định nghĩa: Giải hệ phương trình bằng phương pháp thế là ta sửa dụng phương pháp thế để tìm ra tất cả các nghiệm của phương trình.

Các bước giải hệ phương trình bằng phương pháp thế:

Bước 1: Dùng quy tắc thế biến đổi hệ phương trình đã cho để được một hệ phương trình mới, trong đó có một phương trình một ẩn.

Bước 2: Giải phương trình một ẩn đó rồi suy ra nghiệm của hệ đã cho.

Ví dụ 2: Giải hệ phương trình $\left\{\begin{array}{l}\mathrm{x}-2\mathrm{y}=5\\ 2\mathrm{x}+3\mathrm{y}=6\end{array}\right.$.

Từ ví dụ 1 ta có:

Ta thực hiện các bước rút thế như sau:

$\left\{\begin{array}{l}\mathrm{x}-2\mathrm{y}=5 \left(1\right)\\ 2\mathrm{x}+3\mathrm{y}=6 \left(2\right)\end{array}\right.$

Từ phương trình (1) ta rút được x = 2y + 5 thế vào phương trình (2) ta được:

$$\begin{gathered} \left\{\begin{array}{l}\mathrm{x}-2\mathrm{y}=5\\ 2\left(2\mathrm{y}+5\right)+3\mathrm{y}=6\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2\mathrm{y}+5\\ 4\mathrm{y}+10+3\mathrm{y}=6\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2\mathrm{y}+5\\ 7\mathrm{y}+10=6\end{array}\left(\mathrm{II}\right)\right. \end{gathered}$$

Ta giải tiếp hệ phương trình (II)

$$\begin{gathered} \left\{\begin{array}{l}\mathrm{x}=2\mathrm{y}+5\\ 7\mathrm{y}+10=6\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2\mathrm{y}+5\\ 7\mathrm{y}=6-10\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=2\mathrm{y}+5\\ 7\mathrm{y}=-4\end{array}\right.\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2\mathrm{y}+5\\ \mathrm{y}=\frac{-4}{7}\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2.\left(\frac{-4}{7}\right)+5\\ \mathrm{y}=\frac{-4}{7}\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=\frac{27}{7}\\ \mathrm{y}=\frac{-4}{7}\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) là $(\frac{27}{7};\frac{-4}{7})$

Bài tập tự luyện 

Bài 1: 

Giải các hệ phương trình sau bằng phương pháp thế:

Lời giải

Cách 1

Từ (1) rút ra được y = x – 3

Thế vào phương trình (2) ta được:

3x – 4.(x – 3) = 2 ⇔ 3x – 4x + 12 = 2 ⇔ x = 10

Từ x = 10 ⇒ y = x – 3 = 7.

Vậy hệ phương trình có nghiệm duy nhất (10 ; 7).

Từ (2) rút ra được y = -4x + 2.

Thế y = -4x + 2 vào phương trình (1) ta được :

7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ 

Vậy hệ phương trình có nghiệm duy nhất 

Từ (1) rút x theo y ta được: x = -3y – 2

Thế x = -3y – 2 vào phương trình (2) ta được :

5.(-3y – 2) – 4y = 11 ⇔ -15y – 10 – 4y = 11 ⇔ -19y = 21 ⇔ 

Vậy hệ phương trình có nghiệm duy nhất 

Cách 2: 

a) $\left\{\begin{array}{l}x-y=3\\ 3x-4y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=3+y\\ 3x-4y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=3+y\\ 3\left(3+y\right)-4y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=3+y\\ 9+3y-4y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=y+3\\ 9-y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=y+3\\ y=9-2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=y+3\\ y=7\end{array}\right.$

$\iff \left\{\begin{array}{l}x=7+3\\ y=7\end{array}\right.$

$\iff \left\{\begin{array}{l}x=10\\ y=7\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = (10; 7)

b) $\left\{\begin{array}{l}7x-3y=5\\ 4x+y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}7x-3y=5\\ y=2-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}7x-3.\left(2-4x\right)=5\\ y=2-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}7x-6+12x=5\\ y=2-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}19x=5+6\\ y=2-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}19x=11\\ y=2-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{11}{19}\\ y=2-4.\frac{11}{19}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{11}{19}\\ y=\frac{-6}{19}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{11}{19};\frac{-6}{19}\right)$.

c) $\left\{\begin{array}{l}x+3y=-2\\ 5x-4y=11\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-2-3y\\ 5\left(-2-3y\right)-4y=11\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-2-3y\\ -10-15y-4y=11\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-2-3y\\ -19y=10+11\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-2-3y\\ -19y=21\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-2-3y\\ y=\frac{-21}{19}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-2-3.\left(\frac{-21}{19}\right)\\ y=\frac{-21}{19}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{25}{19}\\ y=\frac{-21}{19}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{25}{19};\frac{-21}{19}\right)$.

Bài 2: Giải các hệ phương trình sau bằng phương pháp thế:

Lời giải

Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.

Cách 1:

Từ (1) ta rút ra được  (*)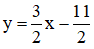

Thế (*) vào phương trình (2) ta được :

Thay x = 7 vào (*) ta suy ra 

Vậy hệ phương trình có nghiệm duy nhất (7 ; 5).

Từ (1) ta rút ra được :  (*)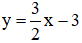

Thế (*) vào phương trình (2) ta được :

Thay x = 3 vào (*) ta suy ra 

Vậy hệ phương trình có nghiệm duy nhất 

Cách 2:

Vậy hệ phương trình có nghiệm duy nhất (7; 5).

Vậy hệ phương trình có nghiệm duy nhất 

Bài 3: Giải các hệ phương trình sau bằng phương pháp thế:

Lời giải

Cách 1: 

a) $\left\{\begin{array}{l}x+y\sqrt{5}=0\text{ (1)}\\ \text{x}\sqrt{5}+3y=1-\sqrt{5}\text{ (2)}\end{array}\right.$

Từ (1) ta rút ra được x = y$\sqrt{5}$(*)

Thế (*) vào phương trình (2) ta được: 

-y$\sqrt{5}.\sqrt{5}$ + 3y = 1 - $\sqrt{5}$

-5y + 3y = 1 - $\sqrt{5}$

-2y = 1 - $\sqrt{5}$

y = $\frac{1-\sqrt{5}}{-2}=\frac{\sqrt{5}-1}{2}$

Thay y = $\frac{\sqrt{5}-1}{2}$ vào (*) ta được: 

x = $-\frac{\sqrt{5}-1}{2}.\sqrt{5}=\frac{\sqrt{5}-5}{2}$

Vậy hệ phương trình có nghiệm (x; y) = $\left(\frac{\sqrt{5}-5}{2};\frac{\sqrt{5}-1}{2}\right)$

b) $\left\{\begin{array}{l}\left(2-\sqrt{3}\right)x-3y=2+5\sqrt{3}\text{ (1)}\\ 4x+y=4-2\sqrt{3}\text{ (2)}\end{array}\right.$

Từ (2) ta rút ra được y = -4x + 4 – 2$\sqrt{3}$ (*)

Thế (*) vào phương trình (1) ta được:

$\left(2-\sqrt{3}\right)x-3\left(-4x+4-2\sqrt{3}\right)=2+5\sqrt{3}$

$\iff \left(2-\sqrt{3}\right)x+12x-12+6\sqrt{3}=2+5\sqrt{3}$

$\iff \left(2-\sqrt{3}+12\right)x=2+5\sqrt{3}+12-6\sqrt{3}$

$\iff \left(14-\sqrt{3}\right)x=14-\sqrt{3}$

$\iff$ x = 1

Thay x = 1 vào (*) ta được y = -4.1 + 4 - 2$\sqrt{3}$ = -2$\sqrt{3}$

Vậy hệ phương trình có nghiệm duy nhất $\left(1;-2\sqrt{3}\right)$.

Cách 2: 

a) $\left\{\begin{array}{l}x+y\sqrt{5}=0\\ x\sqrt{5}+3y=1-\sqrt{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-y\sqrt{5}\\ -y\sqrt{5}.\sqrt{5}+3y=1-\sqrt{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-y\sqrt{5}\\ y\left(-5+3\right)=1-\sqrt{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-y\sqrt{5}\\ -2y=1-\sqrt{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-\sqrt{5}y\\ y=\frac{1-\sqrt{5}}{-2}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-\sqrt{5}y\\ y=\frac{\sqrt{5}-1}{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-\sqrt{5}.\left(\frac{\sqrt{5}-1}{2}\right)\\ y=\frac{\sqrt{5}-1}{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{\sqrt{5}-5}{2}\\ y=\frac{\sqrt{5}-1}{2}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{\sqrt{5}-5}{2};\frac{\sqrt{5}-1}{2}\right)$

b) $\left\{\begin{array}{l}\left(2-\sqrt{3}\right)x-3y=2+5\sqrt{3}\\ 4x+y=4-2\sqrt{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(2-\sqrt{3}\right)x-3y=2+5\sqrt{3}\\ y=4-2\sqrt{3}-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(2-\sqrt{3}\right)x-3.\left(4-2\sqrt{3}-4x\right)=2+5\sqrt{3}\\ y=4-2\sqrt{3}-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(2-\sqrt{3}\right)x-12+6\sqrt{3}+12x=2+5\sqrt{3}\\ y=4-2\sqrt{3}-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(2-\sqrt{3}+12\right)x=2+5\sqrt{3}-6\sqrt{3}+12\\ y=4-2\sqrt{3}-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(14-\sqrt{3}\right)x=14-\sqrt{3}\\ y=4-2\sqrt{3}-4x\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1\\ y=4-2\sqrt{3}-4.1\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1\\ y=-2\sqrt{3}\end{array}\right.$

Vậy phương trình đã cho có nghiệm (x; y) là (1; $-2\sqrt{3}$).

Bài 4: Giải hệ phương trình $\left\{\begin{array}{l}x+3y=1\\ \left(a^2+1\right)x+6y=2a\end{array}\right.$trong mỗi trường hợp sau:

a) a = -1;    b) a = 0;    c) a = 1.

Lời giải

Cách 1

Ta có: 

Từ (1) rút ra được x = 1 – 3y (*)

Thay vào phương trình (2) ta được :

(a² + 1).(1 – 3y) + 6y = 2a

⇔ a² + 1 – 3(a² + 1)y + 6y = 2a

⇔ a² +1- 2a = 3a².y – 6y + 3y

⇔ ( a- 1)² = 3a²y – 3y

⇔ 3(a² – 1).y = (a – 1)² (**)

a) a = -1, phương trình (**) trở thành : 0y = 4

Phương trình trên vô nghiệm

Vậy hệ phương trình khi a = -1 vô nghiệm.

b) a = 0, phương trình (**) trở thành -3y = 1 ⇔ 

Thay 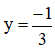 vào (*) ta được x = 2.

Vậy hệ phương trình khi a = 0 có nghiệm duy nhất 

c) a = 1, phương trình (**) trở thành: 0y = 0

Phương trình nghiệm đúng với mọi y.

Vậy hệ phương trình khi a = 1 có vô số nghiệm dạng (1 – 3y; y) (y ∈ R).

Cách 2: 

$\left\{\begin{array}{l}x+3y=1\\ \left(a^2+1\right)x+6y=2a\end{array}\right.$ $\iff \left\{\begin{array}{l}x=1-3y\\ \left(a^2+1\right)\left(1-3y\right)+6y=2a\end{array}\right.$

a) Thay a = -1 vào hệ phương trình ta được

$\left\{\begin{array}{l}x=1-3y\\ \left({\left(-1\right)}^2+1\right)\left(1-3y\right)+6y=2.\left(-1\right)\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 2.\left(1-3y\right)+6y=-2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 2-6y+6y=-2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 2=-2\end{array}\right.$ (vô lí)

Vậy với a = - 1 hệ phương trình đã cho vô nghiệm.

b) Thay a = 0 vào hệ phương trình ta được

$\left\{\begin{array}{l}x=1-3y\\ \left(0^2+1\right)\left(1-3y\right)+6y=2.0\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 1-3y+6y=0\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 3y=-1\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 3y=-1\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3.\left(\frac{-1}{3}\right)\\ y=\frac{-1}{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=2\\ y=\frac{-1}{3}\end{array}\right.$

Vậy với a = 0 hệ phương trình đã cho có nghiệm duy nhất (x; y) = $\left(2;\frac{-1}{3}\right)$

c) Thay a = 1 vào hệ phương trình ta có:

$\left\{\begin{array}{l}x=1-3y\\ \left(1^2+1\right)\left(1-3y\right)+6y=2.1\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 2.\left(1-3y\right)+6y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 2-6y+6y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1-3y\\ 2=2\end{array}\right.$ (luôn đúng)

Vậy với a = 1 hệ phương trình đã cho có vô số nghiệm dạng (1 – 3y; y) với $y\in ℝ$

Bài 5: Giải các hệ phương trình sau bằng phương pháp thế:

Lời giải

a) $\left\{\begin{array}{l}3x-y=5\\ 5x+2y=23\end{array}\right.$

$\iff \left\{\begin{array}{l}y=3x-5\\ 5x+2.\left(3x-5\right)=23\end{array}\right.$

$\iff \left\{\begin{array}{l}5x+6x-10=23\\ y=3x-5\end{array}\right.$

$\iff \left\{\begin{array}{l}11x=23+10\\ y=3x-5\end{array}\right.$

$\iff \left\{\begin{array}{l}11x=33\\ y=3x-5\end{array}\right.$

$\iff \left\{\begin{array}{l}x=33:11\\ y=3x-5\end{array}\right.$

$\iff \left\{\begin{array}{l}x=3\\ y=3.3-5\end{array}\right.$

$\iff \left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm là (x; y) = (3; 4)

b) $\left\{\begin{array}{l}3x+5y=1\\ 2x-y=-8\end{array}\right.$

$\iff \left\{\begin{array}{l}3x+5y=1\\ y=2x+8\end{array}\right.$

$\iff \left\{\begin{array}{l}3x+5\left(2x+8\right)=1\\ y=2x+8\end{array}\right.$

$\iff \left\{\begin{array}{l}3x+10x+40=1\\ y=2x+8\end{array}\right.$

$\iff \left\{\begin{array}{l}13x=1-40\\ y=2x+8\end{array}\right.$

$\iff \left\{\begin{array}{l}13x=-39\\ y=2x+8\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-39:13\\ y=2x+8\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-3\\ y=2.\left(-3\right)+8\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-3\\ y=2\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (-3; 2).

c) $\left\{\begin{array}{l}\frac{x}{y}=\frac{2}{3}\\ x+y-10=0\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{2}{3}y\\ \frac{2}{3}y+y-10=0\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{2}{3}y\\ \frac{5}{3}y=10\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{2}{3}y\\ y=10:\frac{5}{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{2}{3}y\\ y=6\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{2}{3}.6\\ y=6\end{array}\right.$

$\iff \left\{\begin{array}{l}x=4\\ y=6\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = (4; 6).

Bài 6: Giải các hệ phương trình sau bằng phương pháp thế:

Lời giải

Cách 1

Vậy hệ phương trình có nghiệm duy nhất 

Vậy hệ phương trình có nghiệm duy nhất 

Vậy hệ phương trình có nghiệm duy nhất 

Cách 2

a) $\left\{\begin{array}{l}x\sqrt{2}-y\sqrt{3}=1\\ x+y\sqrt{3}=\sqrt{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}x\sqrt{2}-y\sqrt{3}=1\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(\sqrt{2}-y\sqrt{3}\right)\sqrt{2}-y\sqrt{3}=1\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}2-y\sqrt{6}-y\sqrt{3}=1\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}y\left(-\sqrt{6}-\sqrt{3}\right)=1-2\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}y\left(\sqrt{6}+\sqrt{3}\right)=1\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}y=\frac{1}{\sqrt{6}+\sqrt{3}}\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}y=\frac{\sqrt{6}-\sqrt{3}}{3}\\ x=\sqrt{2}-\frac{\sqrt{6}-\sqrt{3}}{3}.\sqrt{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1\\ y=\frac{\sqrt{6}-\sqrt{3}}{3}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(1;\frac{\sqrt{6}-\sqrt{3}}{3}\right)$

b) $\left\{\begin{array}{l}x-2\sqrt{2}y=\sqrt{5}\\ x\sqrt{2}+y=1-\sqrt{10}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ \left(\sqrt{5}+2\sqrt{2}y\right)\sqrt{2}+y=1-\sqrt{10}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ \sqrt{10}+4y+y=1-\sqrt{10}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ 5y=1-\sqrt{10}-\sqrt{10}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ 5y=1-2\sqrt{10}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ y=\frac{1-2\sqrt{10}}{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}.\frac{1-2\sqrt{10}}{5}\\ y=\frac{1-2\sqrt{10}}{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\sqrt{5}+\frac{2\sqrt{2}-2\sqrt{2}.2\sqrt{10}}{5}\\ y=\frac{1-2\sqrt{10}}{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{-3\sqrt{5}+2\sqrt{2}}{5}\\ y=\frac{1-2\sqrt{10}}{3}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{-3\sqrt{5}+2\sqrt{2}}{5};\frac{1-2\sqrt{10}}{3}\right)$.

c) $\left\{\begin{array}{l}\left(\sqrt{2}-1\right)x-y=\sqrt{2}\\ x+\left(\sqrt{2}+1\right)y=1\end{array}\right.$

$\iff \left\{\begin{array}{l}y=\left(\sqrt{2}-1\right)x-\sqrt{2}\\ x+\left(\sqrt{2}+1\right)y=1\end{array}\right.$

$\iff \left\{\begin{array}{l}y=\left(\sqrt{2}-1\right)x-\sqrt{2}\\ x+\left(\sqrt{2}+1\right)\left(\left(\sqrt{2}-1\right)x-\sqrt{2}\right)=1\end{array}\right.$

$\iff \left\{\begin{array}{l}y=\left(\sqrt{2}-1\right)x-\sqrt{2}\\ x+\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)x-\sqrt{2}\left(\sqrt{2}+1\right)=1\end{array}\right.$

$\iff \left\{\begin{array}{l}y=\left(\sqrt{2}-1\right)x-\sqrt{2}\\ x+x-2-\sqrt{2}=1\end{array}\right.$

$\iff \left\{\begin{array}{l}2x=1+2+\sqrt{2}\\ y=\left(\sqrt{2}-1\right)x-\sqrt{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}2x=3+\sqrt{2}\\ y=\left(\sqrt{2}-1\right)x-\sqrt{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{3+\sqrt{2}}{2}\\ y=\left(\sqrt{2}-1\right)\frac{3+\sqrt{2}}{2}-\sqrt{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{3+\sqrt{2}}{2}\\ y=\frac{-1}{2}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{3+\sqrt{2}}{2};\frac{-1}{2}\right)$

Bài 7: 

a) Xác định các hệ số a và b, biết rằng hệ phương trình $\left\{\begin{array}{l}2x+by=-4\\ bx-ay=-5\end{array}\right.$ có nghiệm (1 ; -2).

b) Cũng hỏi như vậy nếu phương trình có nghiệm là $\left(\sqrt{2}-1;\sqrt{2}\right)$

Lời giải

a) Vì hệ phương trình có nghiệm (1; -2) nên x = 1 và y = -2 thỏa mãn cả hai phương trong trong hệ.

Thay x = 1 và y = -2 vào hệ ta được:

$\left\{\begin{array}{l}2.1+b.(-2)=-4\\ b.1-a.(-2)=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}2-2b=-4\\ b+2a=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}-2b=-4-2\\ b+2a=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}-2b=-6\\ b+2a=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}b=3\\ 3+2a=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}2a=-5-3\\ b=3\end{array}\right.$

$\iff \left\{\begin{array}{l}2a=-8\\ b=3\end{array}\right.$

$\iff \left\{\begin{array}{l}a=-4\\ b=3\end{array}\right.$

Vậy để hệ phương trình đã cho có nghiệm là (1; -2) thì a = -4 và b = 3.

b) Vì hệ phương trình có nghiệm $\left(\sqrt{2}-1;\sqrt{2}\right)$ nên x = $\sqrt{2}-1$ và y = $\sqrt{2}$ thỏa mãn cả hai phương trong trong hệ.

Thay x = $\sqrt{2}-1$ và y = $\sqrt{2}$ vào hệ ta được:

$\left\{\begin{array}{l}2.\left(\sqrt{2}-1\right)+b.\sqrt{2}=-4\\ b.\left(\sqrt{2}-1\right)-a.\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}2\sqrt{2}-2+b\sqrt{2}=-4\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}b\sqrt{2}=-4+2-2\sqrt{2}\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}\sqrt{2}b=-2-2\sqrt{2}\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}b=\frac{-2-2\sqrt{2}}{\sqrt{2}}\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ \left(-2-\sqrt{2}\right)\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ -2\sqrt{2}-2+2+\sqrt{2}-a\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ -a\sqrt{2}=-5+2\sqrt{2}+2-2-\sqrt{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ -a\sqrt{2}=-5+\sqrt{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}a=\frac{-5+\sqrt{2}}{-\sqrt{2}}\\ b=-2-\sqrt{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}a=\frac{5\sqrt{2}-2}{2}\\ b=-2-\sqrt{2}\end{array}\right.$

Vậy để hệ phương trình đã cho có nghiệm là $\left(\sqrt{2}-1;\sqrt{2}\right)$ thì a = $\frac{5\sqrt{2}-2}{2}$ và b = -2 - $\sqrt{2}$.

Bài 8: Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3:

P(x) = mx³ + (m – 2)x² – (3n – 5)x – 4n

Lời giải

+ P(x) chia hết cho x + 1

⇔ P(-1) = 0

⇔ m.(-1)³ + (m – 2)(-1)² – (3n – 5).(-1) – 4n = 0

⇔ -m + m – 2 + 3n – 5 – 4n = 0

⇔ -n – 7 = 0

⇔ n = -7 (1)

+ P(x) chia hết cho x – 3

⇔ P(3) = 0

⇔ m.3³ + (m – 2).3² – (3n – 5).3 – 4n = 0

⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0

⇔ 36m – 13n = 3 (2)

Từ (1) và (2) ta có hệ phương trình :

Xem thêm các dạng bài tập toán hay khác:

50 Bài tập Giải bài toán bằng cách lập phương trình (có đáp án năm 2023)

50 Bài tập Hệ thức Vi – ét và ứng dụng (có đáp án năm 2023)

50 Bài tập Phương trình bậc hai một ẩn (có đáp án năm 2023)

50 Bài tập Giải bài toán bằng cách lập hệ phương trình (có đáp án năm 2023)

50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2023)