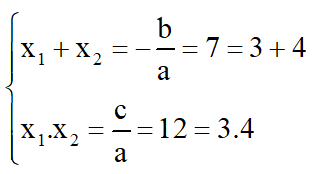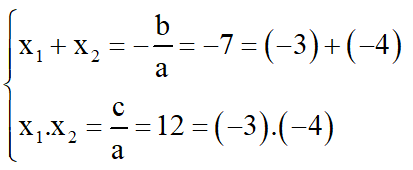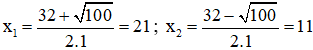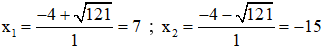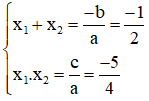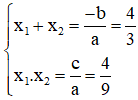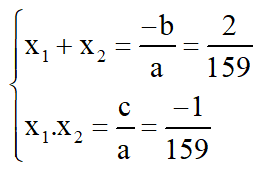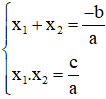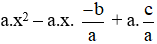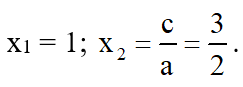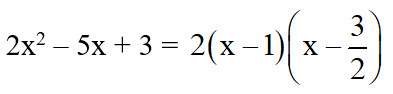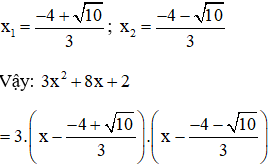50 Bài tập Hệ thức Vi – ét và ứng dụng (có đáp án năm 2023) - Toán 9

Kiến thức cần nhớ 

I. Lý thuyết

1. Hệ thức Vi – ét

Phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có nghiệm dù đó là hai nghiệm phân biệt hay nghiệm kép thì ta đều có thể viết được dưới dạng:

${\mathrm{x}}_1=\frac{-\mathrm{b}+\sqrt{∆}}{2\mathrm{a}}; {\mathrm{x}}_2=\frac{-\mathrm{b}+\sqrt{∆}}{2\mathrm{a}}$

Định lí Vi – ét

Nếu x₁, x₂ là hai nghiệm của phương trình ax² + bx + c = 0 (a ≠ 0) thì ta có:

$\left\{\begin{array}{l}{\mathrm{x}}_1+{\mathrm{x}}_2=\frac{-\mathrm{b}}{\mathrm{a}}\\ {\mathrm{x}}_1.{\mathrm{x}}_2=\frac{\mathrm{c}}{\mathrm{a}}\end{array}\right.$

Nhận xét: Nhờ định lý Vi – ét, nếu đã biết một nghiệm của phương trình bậc hai thì có thế suy ra nghiệm kia.

2. Ứng dụng của định lý Vi – ét.

a) Ứng dụng trong giải phương trình (bằng cách nhẩm miệng)

+ Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x₁ = 1 và nghiệm còn lại là x₂ =$\frac{\mathrm{c}}{\mathrm{a}}$

+ Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a - b + c = 0 thì phương trình có một nghiệm là x₁ = -1 và nghiệm còn lại là x₂ = -$\frac{\mathrm{c}}{\mathrm{a}}$

b) Tìm hai số khi biết tổng và tích.

+ Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình bậc hai x² - Sx + P = 0

+ Điều kiện để có hai số đó là S² - 4P ≥ 0

Bài tập tự luyện 

Bài 1: Đối với mỗi phương trình sau, kí hiệu x₁ và x₂ là hai nghiệm (nếu có). Không giải phương trình, hãy điền vào những chỗ trống (...):

a) 2x² – 17x + 1 = 0;

Δ = …; x₁ + x₂ = …; x₁.x₂ = …;

b) 5x² – x – 35 = 0;

Δ = …; x₁ + x₂ = …; x₁.x₂ = …;

c) 8x² – x + 1 = 0 ;

Δ = …; x₁ + x₂ = …; x₁.x₂ = …;

d) 25x² + 10x + 1 = 0 ;

Δ = …; x₁ + x₂ = …; x₁.x₂ = …;

Lời giải

a) 2x² – 17x + 1 = 0

Có a = 2; b = -17; c = 1

Δ = b² – 4ac = (-17)² – 4.2.1 = 281 > 0.

Theo hệ thức Vi-et: phương trình có hai nghiệm x₁; x₂ thỏa mãn:

x₁ + x₂ = $\frac{-b}{a}$ = $\frac{17}{2}$

x₁.x₂ = $\frac{c}{a}$ = $\frac{1}{2}$.

b) 5x² – x – 35 = 0

Có a = 5; b = -1; c = -35;

Δ = b² – 4ac = (-1)² – 4.5.(-35) = 701 > 0

Theo hệ thức Vi-et, phương trình có hai nghiệm x₁; x₂ thỏa mãn:

x₁ + x₂ = $\frac{-b}{a}$ = $\frac{-\left(-1\right)}{5}$ = $\frac{1}{5}$

x₁.x₂ = $\frac{c}{a}$ = $\frac{-35}{5}$ = -7.

c) 8x² – x + 1 = 0

Có a = 8; b = -1; c = 1

Δ = b² – 4ac = (-1)² – 4.8.1 = -31 < 0

Phương trình vô nghiệm nên không tồn tại x₁ ; x₂.

d) 25x² + 10x + 1 = 0

Có a = 25; b = 10; c = 1

Δ = b² – 4ac = 10² – 4.25.1 = 0

Khi đó theo hệ thức Vi-et có:

x₁ + x₂ = $\frac{-b}{a}$ = $\frac{-10}{25}$ = $\frac{-2}{5}$

x₁.x₂ = $\frac{c}{a}$ = $\frac{1}{25}$.

Bài 2: Dùng điều kiện a + b + c = 0 hoặc a – b + c = 0 để tính nhẩm nghiệm của mỗi phương trình sau:

a) 35x² – 37x + 2 = 0;

b) 7x² + 500x – 507 = 0;

c) x² – 49x – 50 = 0;

d) 4321x² + 21x – 4300 = 0.

Lời giải

a) Phương trình 35x² – 37x + 2 = 0

Có a = 35; b = -37; c = 2 ⇒ a + b + c = 0

⇒ Phương trình có nghiệm x₁ = 1; x₂ = $\frac{c}{a}$ = $\frac{2}{35}$.

Vậy tập nghiệm của phương trình là S = $\left\{1;\frac{2}{35}\right\}$

b) Phương trình 7x² + 500x – 507 = 0

Có a = 7; b = 500; c = -507 ⇒ a + b + c = 7 + 500 – 507 = 0

⇒ Phương trình có nghiệm x₁ = 1; x₂ = $\frac{c}{a}$ = $\frac{-507}{7}$.

Vậy tập nghiệm của phương trình là S = $\left\{1;\frac{-507}{7}\right\}$

c) Phương trình x² – 49x – 50 = 0

Có a = 1; b = -49; c = -50 ⇒ a – b + c = 1 – (-49) – 50 = 0

⇒ Phương trình có nghiệm x₁ = -1; x₂ = $\frac{-c}{a}$ = $\frac{-\left(-50\right)}{1}=50$.

Vậy tập nghiệm của phương trình là S = $\left\{-1;50\right\}$

d) Phương trình 4321x² + 21x – 4300 = 0

Có a = 4321; b = 21; c = -4300 ⇒ a – b + c = 4321 – 21 – 4300 = 0

⇒ Phương trình có nghiệm x₁ = -1; x₂ = $\frac{-c}{a}$ = $\frac{-\left(-4300\right)}{4321}=\frac{4300}{4321}$.

Vậy tập nghiệm của phương trình là S = $\left\{-1;\frac{4300}{4321}\right\}$

Bài 3: Dùng hệ thức Vi-et để tính nhẩm các nghiệm của phương trình.

a) x² – 7x + 12 = 0;

b) x² + 7x + 12 = 0.

Lời giải

a) x² – 7x + 12 = 0

Có a = 1; b = -7; c = 12

⇒ Δ = b² – 4ac = (-7)² – 4.1.12 = 1 > 0

⇒ Phương trình có hai nghiệm phân biệt x₁; x₂ thỏa mãn:

Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.

b) x² + 7x + 12 = 0

Có a = 1; b = 7; c = 12

⇒ Δ = b² – 4ac = 7² – 4.1.12 = 1 > 0

⇒ Phương trình có hai nghiệm phân biệt x₁; x₂ thỏa mãn:

Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.

Bài 4: Tìm hai số u và v trong mỗi trường hợp sau:

a) u + v = 32 , uv = 231

b) u + v = -8, uv = -105

c) u + v = 2, uv = 9

Lời giải

a) S = 32; P = 231 ⇒ S² – 4P = 32² – 4.231 = 100 > 0

⇒ Tồn tại u và v là hai nghiệm của phương trình: x² – 32x + 231 = 0.

Ta có: Δ = (-32)² – 4.231 = 100 > 0

⇒ PT có hai nghiệm:

Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.

b) S = -8; P = -105 ⇒ S² – 4P = (-8)² – 4.(-105) = 484 > 0

⇒ u và v là hai nghiệm của phương trình: x² + 8x – 105 = 0

Ta có: Δ’ = 4² – 1.(-105) = 121 > 0

Phương trình có hai nghiệm:

Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.

c) S = 2 ; P = 9 ⇒ S² – 4P = 2² – 4.9 = -32 < 0

⇒ Không tồn tại u và v thỏa mãn.

Bài 5: Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:

a) 4x² + 2x – 5 = 0;

b) 9x² – 12x + 4 = 0;

c) 5x² + x + 2 = 0;

d) 159x² – 2x – 1 = 0.

Lời giải

a) Phương trình 4x² + 2x – 5 = 0

Có a = 4; b = 2; c = -5, a.c < 0

⇒ Phương trình có hai nghiệm x₁; x₂

Theo hệ thức Vi-et ta có: 

b) Phương trình 9x² – 12x + 4 = 0

Có a = 9; b' = -6; c = 4 ⇒ Δ’ = (-6)² – 4.9 = 0

⇒ Phương trình có nghiệm kép x₁ = x₂.

Theo hệ thức Vi-et ta có: 

c) Phương trình 5x² + x + 2 = 0

Có a = 5; b = 1; c = 2 ⇒ Δ = 1² – 4.2.5 = -39 < 0

⇒ Phương trình vô nghiệm.

d) Phương trình 159x² – 2x – 1 = 0

Có a = 159; b = -2; c = -1; a.c < 0

⇒ Phương trình có hai nghiệm phân biệt x₁; x₂.

Theo hệ thức Vi-et ta có: 

Bài 6: Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.

a) x² – 2x + m = 0;

b) x² + 2(m – 1)x + m² = 0.

Lời giải

a) Phương trình x² – 2x + m = 0

Có a = 1; b = -2; c = m nên b’= -1

⇒ Δ’ = (-1)² – 1.m = 1 – m

Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.

Theo hệ thức Vi-et ta có: $\left\{\begin{array}{l}{x}_1+x_2=\frac{-b}{a}=\frac{-\left(-2\right)}{1}=\frac{2}{1}=2\\ x_1.x_2=\frac{c}{a}=\frac{m}{1}=m\end{array}\right.$

Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.

b) Phương trình x² + 2(m – 1)x + m² = 0

Có a = 1; b = 2(m – 1); c = m² nên b’ = m - 1

⇒ Δ’ = b'² – ac = (m – 1)² – m² = $m^2-2m+1$ - m²= - 2m + 1.

Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ 2m ≤ 1 $\iff m\le \frac{1}{2}$

Theo hệ thức Vi-et ta có: $\left\{\begin{array}{l}{x}_1+x_2=\frac{-b}{a}=\frac{-2\left(m-1\right)}{1}=-2\left(m-1\right)\\ x_1.x_2=\frac{c}{a}=\frac{m^2}{1}=m^2\end{array}\right.$

Vậy với m ≤ $\frac{1}{2}$, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m².

Bài 7: Tính nhẩm nghiệm của các phương trình:

a) $1,5x^2-1,6x+0,1=0$

b) $\sqrt{3}{x}^2-\left(1-\sqrt{3}\right)x-1=0$

c) $\left(2-\sqrt{3}\right)x^2+2\sqrt{3}x-\left(2+\sqrt{3}\right)=0$

d) $\left(m-1\right)x^2-\left(2m+3\right)x+m+4=0$ với $m\ne 1$

Lời giải

a) 1,5x² – 1,6x + 0,1 = 0

Có a = 1,5; b = -1,6; c = 0,1

⇒ a + b + c = 1,5 – 1,6 + 0,1 = 0

⇒ Phương trình có hai nghiệm x₁ = 1; x₂ = $\frac{c}{a}$ = $\frac{0,1}{1,5}$ = $\frac{1}{15}$.

Vậy phương trình đã cho có tập nghiệm $S=\left\{1;\frac{1}{15}\right\}$

b)$\sqrt{3}{x}^2-\left(1-\sqrt{3}\right)x-1=0$

Ta có: a = $\sqrt{3}$; b = $-\left(1-\sqrt{3}\right)$; c = -1.

$\Rightarrow a-b+c=\sqrt{3}+1-\sqrt{3}-1=0$.

Phương trình có hai nghiệm phân biệt

$x_1=-1;x_2=\frac{-c}{a}=\frac{-\left(-1\right)}{\sqrt{3}}=\frac{\sqrt{3}}{3}$

Vậy phương trình đã cho có tập nghiệm $S=\left\{-1;\frac{\sqrt{3}}{3}\right\}$

c) $\left(2-\sqrt{3}\right)x^2+2\sqrt{3}x-\left(2+\sqrt{3}\right)=0$

Ta có a = 2 - $\sqrt{3}$; b = 2$\sqrt{3}$; c = $-\left(2+\sqrt{3}\right)$

$\Rightarrow a+b+c=\left(2-\sqrt{3}\right)+2\sqrt{3}-\left(2+\sqrt{3}\right)$

$\iff a+b+c=2-\sqrt{3}+2\sqrt{3}-2-\sqrt{3}$ = 0

Phương trình có hai nghiệm phân biệt:

$x_1=1;x_2=\frac{c}{a}=\frac{-\left(2+\sqrt{3}\right)}{2-\sqrt{3}}=-7-4\sqrt{3}$

Vậy tập nghiệm của phương trình là $S=\left\{-7-4\sqrt{3};1\right\}$

d) $\left(m-1\right)x^2-\left(2m+3\right)x+m+4=0$

Có a = m – 1; b = -(2m + 3); c = m + 4

⇒ a + b + c = (m – 1) – (2m + 3) + m + 4 = m - 1 – 2m – 3 + m + 4 = 0

⇒ Phương trình có hai nghiệm $x_1=1;x_2=\frac{c}{a}=\frac{m+4}{m-1}$ với m $\ne 1$.

Vậy tập nghiệm của phương trình là $S=\left\{1;\frac{m+4}{m-1}\right\}$.

Bài 8: Tìm hai số u và v trong mỗi trường hợp sau:

a) u + v = 42, uv = 441

b) u + v = -42, uv = -400

c) u – v = 5, uv = 24

Lời giải

a) S = 42; P = 441 ⇒ S² – 4P = 42² – 4.441 = 0

⇒ u và v là hai nghiệm của phương trình: x² – 42x + 441 = 0

Có: Δ’ = (-21)² – 441 = 0

⇒ Phương trình có nghiệm kép x₁ = x₂ = $\frac{-b}{2a}=\frac{-\left(-42\right)}{2}=21$.

Vậy u = v = 21.

b) S = -42; P = -400 ⇒ S² – 4P = (-42)² – 4.(-400) = 3364 > 0

⇒ u và v là hai nghiệm của phương trình: x² + 42x – 400 = 0

Có Δ’ = 21² – 1.(-400) = 841

⇒ Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-21+\sqrt{841}}{1}=8$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-21-\sqrt{841}}{1}=-50$

Vậy u = 8; v = -50 hoặc u = -50; v = 8.

c) u – v = 5 ⇒ u + (-v) = 5

u.v = 24 ⇒ u.(-v) = -uv = -24.

Ta tìm u và –v. Từ đó, ta dễ dàng tính được u và v.

S = u + (-v) = 5; P = u. (-v) = -24 ⇒ S² – 4P = 5² – 4.(-24) = 121 > 0

⇒ u và –v là hai nghiệm của phương trình: x² – 5x – 24 = 0

Có Δ = (-5)² – 4.1.(-24) = 121

⇒ Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{5+\sqrt{121}}{1.2}=8$;

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{5-\sqrt{121}}{1.2}=-3$

+) Với u = 8 thì –v = -3

$\Rightarrow u=8;v=3$

+) Với u = -3 thì -v = 8

$\Rightarrow u=-3;v=-8$ .

Vậy u = 8 thì v = 3 hoặc u = -3 và v = -8

Bài 9: Chứng tỏ rằng nếu phương trình ax² + bx + c = 0 có nghiệm là x₁ và x₂ thì tam thức ax² + bx + c phân tích được thành nhân tử như sau:

ax² + bx + c = a( x - x₁)(x - x₂)

Áp dụng : phân tích đa thức thành nhân tử.

a) 2x² - 5x + 3;    b)3x² + 8x + 2

Lời giải

* Chứng minh:

Phương trình ax² + bx + c = 0 có hai nghiệm x₁; x₂

⇒ Theo định lý Vi-et: 

Khi đó : a.(x – x₁).(x – x₂)

= a.(x² – x₁.x – x₂.x + x₁.x₂)

= a.x² – a.x.(x₁ + x₂) + a.x₁.x₂

= 

= a.x² + bx + c (đpcm).

* Áp dụng:

a) 2x² – 5x + 3 = 0

Có a = 2; b = -5; c = 3

⇒ a + b + c = 2 – 5 + 3 = 0

⇒ Phương trình có hai nghiệm 

Vậy: 

b) 3x² + 8x + 2 = 0

Có a = 3; b' = 4; c = 2

⇒ Δ’ = 4² – 2.3 = 10 > 0

⇒ Phương trình có hai nghiệm phân biệt: