Cách chứng minh tam giác vuông cân
I. Phương pháp giải
Từ định nghĩa về tam giác vuông cân ta có các cách chứng minh tam giác vuông cân như sau:
-Tam giác có 1 góc vuông và 2 cạnh góc vuông bằng nhau là tam giác vuông cân
-Tam giác vuông có 1 góc nhọn bằng 45 độ
-Tam giác có 2 cạnh bằng nhau và 1 góc đáy bằng 45 độ
Ví dụ minh họa
VD1: Vẽ 1 tam giác vuông cân
Đáp án:
Giả sử cần vẽ tam giác ABC vuông cân tại A
- Vẽ góc vuông xAy trên hệ trục xAy
- Trên tia Ay lấy điểm C Trên tia Ax lấy điểm B, sao cho AC = AB
- Nối điểm B với C
- Như vậy ta được tam giác ABC vuông cân tại A.
VD2: Cho tam giác ABC cân tại A (Â < 90º). Vẽ CK ⊥ AB (K ∈ AB) BH ⊥ AC (H ∈ AC)
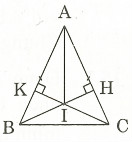
a) Chứng minh: AH = AK
b) Gọi I là giao điểm của CK và BH. Chứng minh: AI chính là tia phân giác của góc A.
Đáp án:
ΔACk = ΔABH ⇒ AK = AH
ΔAIK = ΔAIH (cạnh huyền – cạnh góc vuông)
⇒ IÂK = IÂH ⇒ AI là tia phân giác từ góc A.
VD3: Tam giác ABC có đường cao BE và CF cắt nhau tại O, Biết AB= OC
-
Chứng minh tam giác OEC = tam giác AEB
-
Tính số đo góc ACB
Đáp án
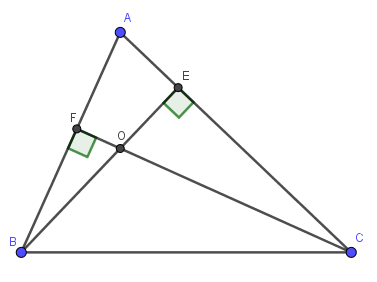
a)Xét ΔOEC và Δ AEB
Ta có góc ^AEB = ^BEC = 90 độ
Theo giả thiết: AB= OC
Góc ^ABE = ^ECO (vì cùng phụ với góc A)
Vì vậy: ΔOEC = Δ AEB (c.g.c)
b) Vì tam giác ECB vuông cân tại E nên góc ^ACB = 45 độ
II. Bài tập vận dụng
Bài 1: Hãy cho biết cần thêm điều kiện gì để
a, Tam giác vuông trở thành tam giác vuông cân
b, Tam giác cân trở thành tam giác vuông cân
Bài 2: Cho tam giác ABC, biết góc . Tính số đo các góc còn lại của tam giác đó.
Bài 3: Cho tam giác ABC cân tại A. Lấy điểm D và E lần lượt là trung điểm của AB và AC. Chứng minh BE = CD
Bài 4: Cho tam giác ABC cân ở A. Trên cạnh BC lấy D, E sao cho BD = CE. Chứng minh tam giác ADE là tam giác cân
Bài 5: Cho tam giác ABC có
a, Chứng minh tam giác ABC cân
b, Đường thẳng song song với BC cắt tia đối của tia AB ở D, cắt tia đối của tia AC ở E. Chứng minh tam giác ADE cân
Bài 6: Cho tam giác vuông cân ABC tại A, tia phân giác của các góc B và C cắt AC và AB lần lượt tại E và D
a, Chứng minh rằng BE = CD, AD = AE
b, Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh rằng các tam giác MAB và MAC là tam giác vuông cân
Hướng dẫn giải
Bài 1:
a, Gọi là tam giác vuông, tức là
Để trở thành tam giác vuông cân tại A thì hai cạnh góc vuông AB = AC
b, Gọi là tam giác cân tại A, tức là ta có AB = AC
Để trở thành tam giác vuông cân tại A thì
Bài 2:
Có là tam giác cân tại A
Lại có theo đề bài
Xét có
(tổng 3 góc trong 1 tam giác)
Bài 3:
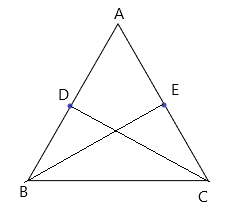
Xét tam giác ABC cân tại A, có và AB = AC
Có D là trung điểm của AB AD = BD
Có E là trung điểm của AC AE = EC
Từ đó ta có AD = BD = AE = EC
Xét tam giác BDC và tam giác CEB có:
BD = CE (cmt)
(cmt)
BC chung
Hai tam giác BDC và tam giác CEB bằng nhau (theo trường hợp c - g - c)
BE = CD (cặp cạnh tương ứng)
Bài 4:
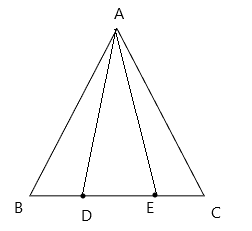
Xét tam giác ABD và tam giác ACE có:
AB = AC (do tam giác ABC cân tại A)
(do tam giác ABC cân tại A)
BD = EC (giả thiết)
(cặp cạnh tương ứng)
Xét tam gác ADE có AD = AE (cmt). Suy ra tam giác ADE là tam giác cân tại A
Bài 5: Học sinh tự vẽ hình
a, Xét tam giác ABC có: (tổng ba góc trong một tam giác)
Có Tam giác ABC là tam giác cân tại A
b, Co ED// BC
(vị trí so le trong) và
(vị trí so le trong)
Mà
Suy ra Tam giác ADE cân tại A
Bài 6: Học sinh tự vẽ hình
a, Vì tam giác ABC cân tại A nên AB = AC và
Vì BE là tia phân giác của góc B nên
Và CD là tia phân giác của góc C nên
Và nên
Xét tam giác BEA và tam giác CDA có:
chung
AB = AC (gt)
Suy ra tam giác BEA bằng với tam giác CDA (theo trường hợp g-c-g)
Suy ra BE = CD và AD = AE (cặp cạnh tương ứng)
b, Có
Xét tam giác AID và tam giác AIE có:
AI chung
Suy ra tam giác AID bằng tam giác AIE (theo trường hợp c-g-c)
Suy ra (hai góc tương ứng)
Lại có
Suy ra hai tam giác AMB và AMC là hai tam giác vuông cân
Xem thêm các dạng bài tập hay, có đáp án:
30 Bài tập đường trung tuyến trong tam giác vuông cân (2024) hay, có đáp án
70 Bài tập Tam giác cân. Tam giác đều (có đáp án năm 2024)
30 bài tập Tam giác đều. Hình vuông. Lục giác đều (2024) hay nhất, có đáp án
30 Bài tập về Trực tâm của tam giác mới nhất (2024) có đáp án
50 Bài tập Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án năm 2024)




