70 Bài tập Tam giác cân. Tam giác đều
Kiến thức cần nhớ
1. Tam giác cân:
a. Định nghĩa:
Tam giác cân là tam giác có hai cạnh bằng nhau.
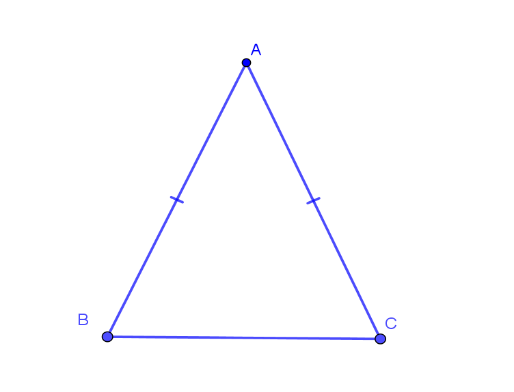
Trên hình, tam giác ABC cân ở A (AB = AC), AB và AC là hai cạnh bên, BC là cạnh đáy, ˆB, ˆC là các góc ở đáy, ˆA là góc ở đỉnh.
b. Tính chất:
- Trong tam giác cân, hai góc ở đáy bằng nhau. Ngược lại, tam giác có hai góc bằng nhau là tam giác cân.
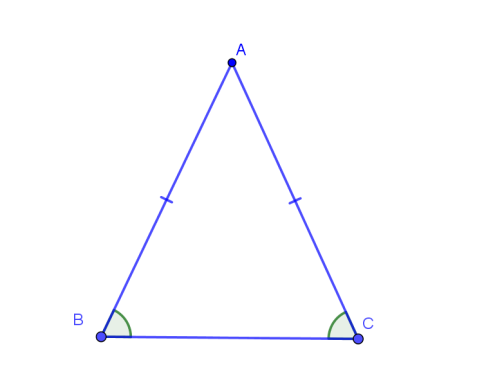
- Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.
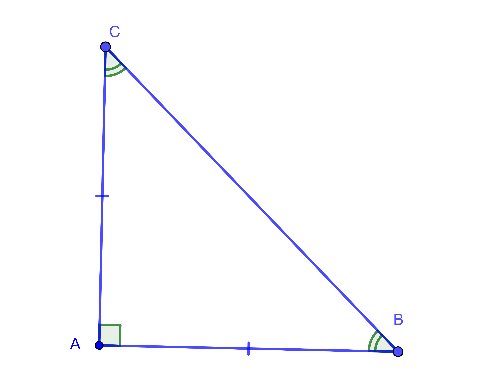
Tam giác ABC vuông cân tại A thì ˆB=ˆC=45o
2. Tam giác đều.
Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.
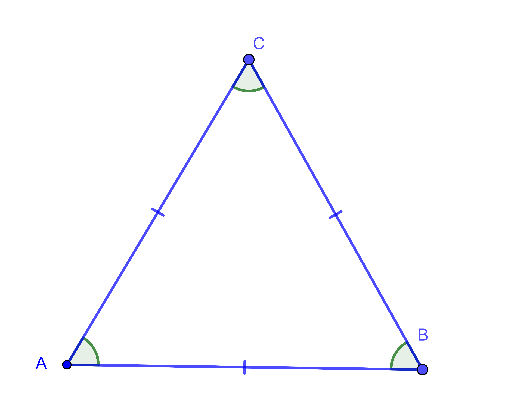
Tam giác ABC đều thì AB = AC = BC và ˆA=ˆB=ˆC=60o
Hệ quả:
- Trong tam giác đều, mỗi góc bằng 60°.
- Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
- Nếu một tam giác cân có một góc bằng 60° thì tam giác đó là tam giác đều.
Các dạng bài tập về Tam giác cân. Tam giác đều
Dạng 1: Cách vẽ tam giác cân, vuông cân, tam giác đều.
1. Phương pháp giải:
Dựa vào các cách vẽ tam giác đã học và định nghĩa các tam giác cân, vuông cân, đều.
2. Ví dụ minh họa:
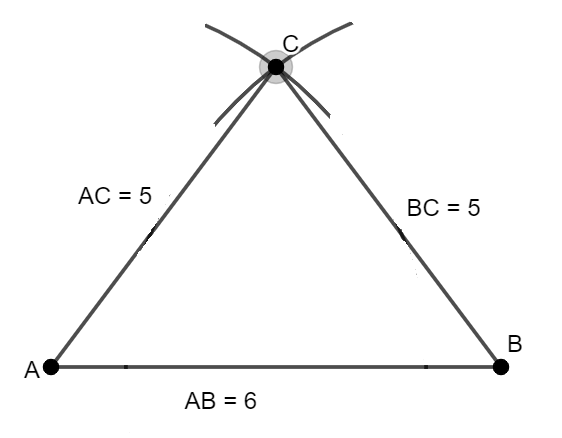
Ví dụ 1: Vẽ tam giác ABC cân tại C có AB = 6 cm, AC = BC = 5cm.
Giải: (Vẽ tương tự như cách vẽ tam giác thường biết độ dài ba cạnh)
Cách vẽ:
- Vẽ đoạn thẳng AB = 6cm.
- Vẽ cung tròn tâm A bán kính 5cm.
- Vẽ cung tròn tâm B bán kính 5cm.
- Hai cung tròn này cắt nhau tại C.
- Nối CA, CB ta được tam giác ABC cần vẽ.
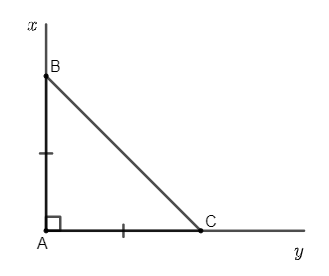
Ví dụ 2: Vẽ tam giác ABC vuông cân tại A.
Giải:
- Vẽ góc vuông xAy
- Trên tia Ax lấy điểm B, trên tia Ay lấy điểm C sao cho AB = AC
- Nối B với C
- Khi đó ta được tam giác ABC vuông cân tại A.
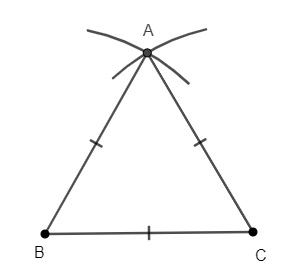
Ví dụ 3: Vẽ tam giác đều ABC có cạnh bằng 4 cm.
Giải:
- Vẽ đoạn thẳng BC = 4 cm
- Vẽ cung tròn tâm B bán kính 4 cm.
- Vẽ cung tròn tâm C bán kính 4 cm.
- Hai cung tròn này cắt nhau tại A.
- Nối AB, AC ta được tam giác ABC cần vẽ.
Dạng 2: Nhận biết một tam giác là tam giác cân, vuông cân, đều.
1. Phương pháp giải:
Những dấu hiệu nhận biết các tam giác cân, vuông cân, đều:
*Tam giác cân:
- Tam giác cân là tam giác có hai cạnh bằng nhau (theo định nghĩa).
- Tam giác có hai góc bằng nhau là tam giác cân.
*Tam giác vuông cân:
- Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau (theo định nghĩa).
- Tam giác vuông có một góc nhọn bằng 45o là tam giác vuông cân.
*Tam giác đều:
- Tam giác đều là tam giác có ba cạnh bằng nhau (theo định nghĩa).
- Tam giác có ba góc bằng nhau là tam giác đều.
- Tam giác cân có một góc bằng 60° là tam giác đều.
2. Ví dụ minh họa:
Ví dụ 4: Tìm các tam giác cân, vuông cân, đều trên hình vẽ sau:
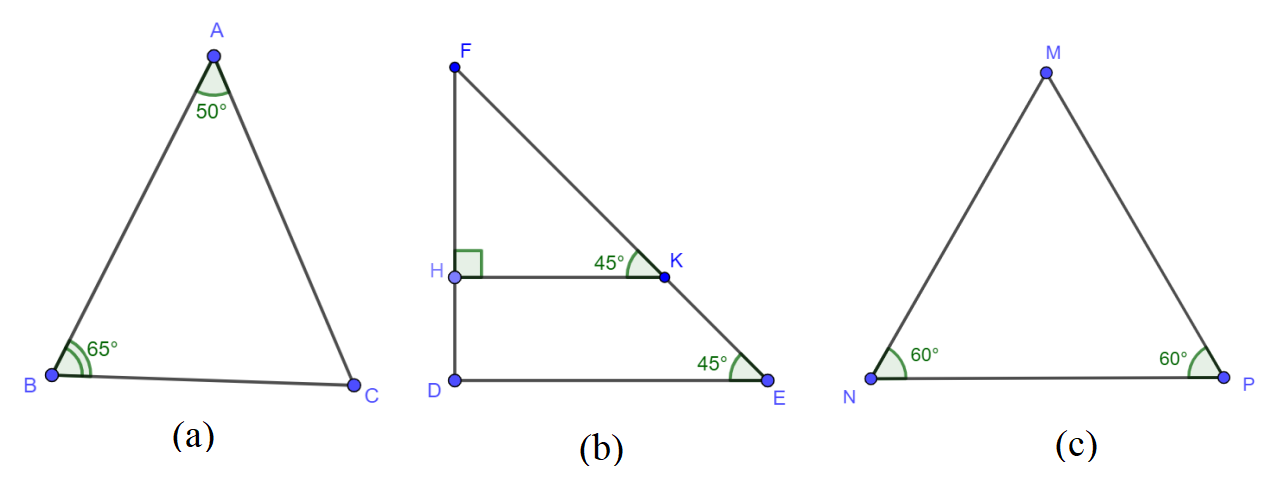
Giải:
(a) Áp dụng định lý góc ngoài trong tam giác ABC có:
ˆA+ˆB+ˆC=180o ⇒ˆC=180o−ˆA−ˆB
⇒ˆC=180o−50o−65o=65o
ΔABC có ˆB=ˆC=65o
Do đó ΔABC cân tại A.
(b) Ta có, ΔHKF vuông tại H có ˆK=45o
Nên ΔHKF là tam giác vuông cân tại H (1)
Vì ^DEF=^HKF=45o
Mà hai góc này ở vị trí so le trong nên HK // DE
Vì HK⊥HF, HK // DE
⇒DE⊥DF (Tính chất từ vuông góc đến song song)
Ta có, ΔDEF vuông tại D có ˆE=45o
Nên ΔDEF là tam giác vuông cân tại D (2)
Từ (1) và (2) suy ra ΔHKF, ΔDEF là tam giác vuông cân.
(c) Áp dụng định lý tổng ba góc trong tam giác MNP có:
ˆM+ˆN+ˆP=180o⇒ˆM=180o−ˆN−ˆP
⇒ˆM=180o−60o−60o=60o
Ta có, ΔMNP có ˆM=ˆN=ˆP (=60o)
Do đó ΔMNP là tam giác đều.
Dạng 3: Sử dụng định nghĩa, tính chất tam giác cân, vuông cân, đều để suy ra các đoạn thẳng, các góc bằng nhau.
1. Phương pháp giải:
Dựa vào định nghĩa và tính chất của tam giác cân, vuông cân, đều.
2. Ví dụ minh họa:
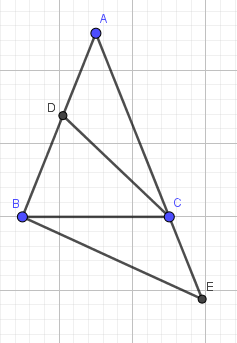
Ví dụ 5: Cho tam giác ABC cân tại A (BC < AB). Trên cạnh AB lấy D sao cho CD = CB.
a) Chứng minh: ^ACB=^CDB.
b) Trên tia đối của tia CA lấy E sao cho CE = AD. Chứng minh BE = BA.
Giải:
|
GT |
Cho ΔABC, AB = AC (BC < AB) CD = CB (D CE là tia đối của tia CA: CE = AD |
|
KL |
a) ^ACB=^CDB b) BE = BA |
a) ΔABC cân tại A nên ^ABC=^ACB (1)
Vì ΔBCD cân tại C (do CD = CB) nên ^CDB=^DBC= ^ABC (2)
Từ (1) và (2) suy ra ^ACB=^CDB
b) Ta có: ^ACB+^BCE=180o
^CDB+^ADC=180o
Mà ^ACB=^CDB (câu a)
Do đó: ^ADC=^BCE
Xét ΔADC và ΔECB có:
CE = AD (gt)
^ADC=^BCE (cmt)
CD = CB (gt)
Do đó: ΔADC=ΔECB (c.g.c)
⇒BE=AC (hai cạnh tương ứng)
Mà AC = AB (do tam giác ABC cân tại A)
Vậy BE = AB (đpcm).
Dạng 4: Tính độ dài đoạn thẳng, tính số đo góc.
1. Phương pháp giải:
Dựa vào định lý tổng ba góc của một tam giác và mối quan hệ giữa các cạnh, các góc trong tam giác đó.
2. Ví dụ minh họa:
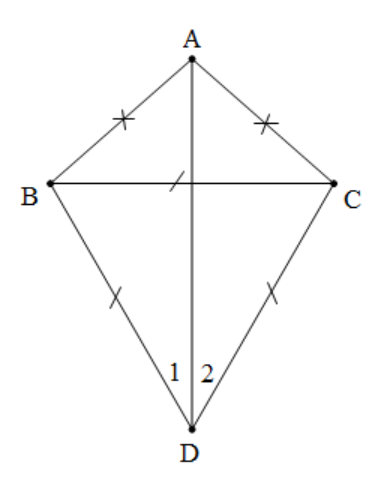
Ví dụ 6: Cho tam giác ABC cân tại A và tam giác đều BCD (D và A nằm khác phía đối với BC). Tính số đo góc BDA.
Giải:
|
GT |
ΔABC, AB=AC ΔBCD, BC=BD=CD (D và A nằm khác phía đối với BC) |
|
KL |
^BDA=? |
Xét ΔABD và ΔACD có:
AB = AC (ΔABC cân)
BD = CD (ΔBCD đều)
Cạnh AD chung
Do đó: ΔABD=ΔACD (c.c.c)
⇒ˆD1=ˆD2 (hai góc tương ứng)
Mặt khác, ΔBCD đều nên ^BDC=60o=ˆD1+ˆD2
⇒ˆD1=ˆD2=30o
Vậy ^BDA=30o.
Bài tập tự luyện
Bài 1: Câu nào đúng, câu nào sai? ( Đánh dấu x vào câu lựa chọn)
|
|
Đúng |
Sai |
|
a) Tam giác cân có một góc 45o là tam giác vuông cân. |
|
|
|
b) Mỗi góc ngoài của 1 tam giác thì bằng tổng 2 góc không kề nó của tam giác đó. |
|
|
|
c) Nếu tam giác có 1 cặp cạnh không bằng nhau thì tam giác đó không phải là tam giác cân. |
|
|
Bài 2: Cho tam giác ABC cân tại A, có ˆA=50o. Tính các góc còn lại của tam giác đó.
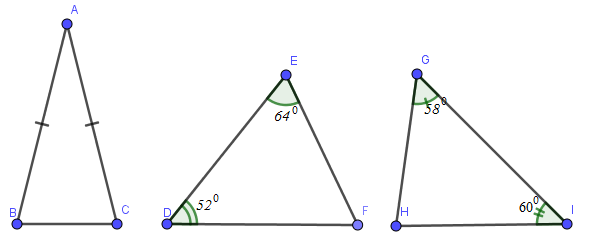
Bài 3: Số tam giác cân ở hình sau là:
A. 0
B. 1
C. 2
D. 3
Bài 4: Cho ∆ABC cân tại A. Lấy điểm E và F lần lượt thuộc các cạnh AB, AC sao cho BE = CF. Chứng minh ΔAEF là tam giác cân.
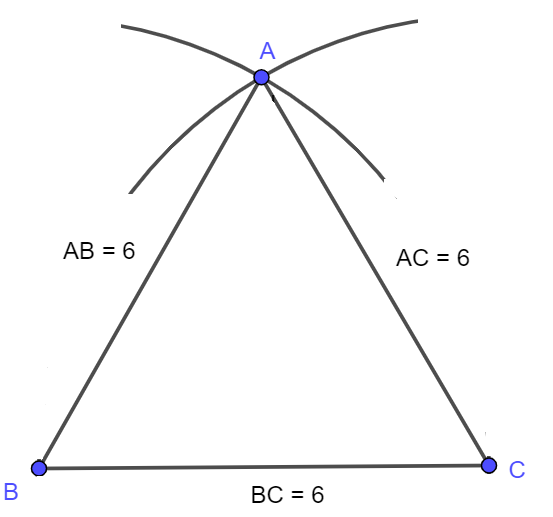
Bài 5: Vẽ tam giác đều ABC có AB = AC = BC = 6cm
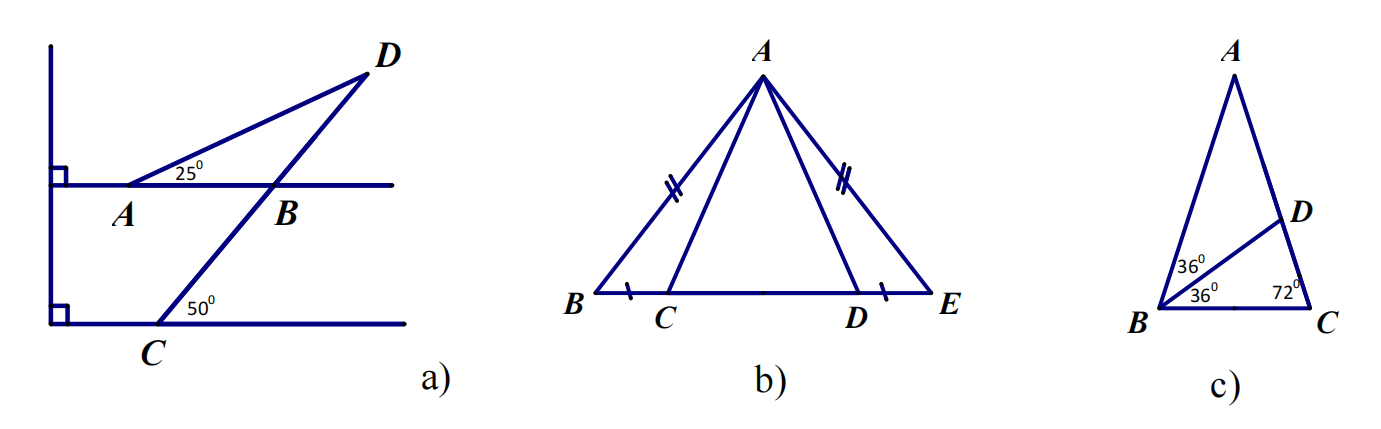
Bài 6: Tìm các tam giác cân trên hình vẽ sau:
Bài 7: Hai đường cao BE và CF của tam giác ABC cắt nhau tại O. Biết OC = AB.
a) Chứng minh ΔAEB=ΔOEC.
b) Tính góc ACB.
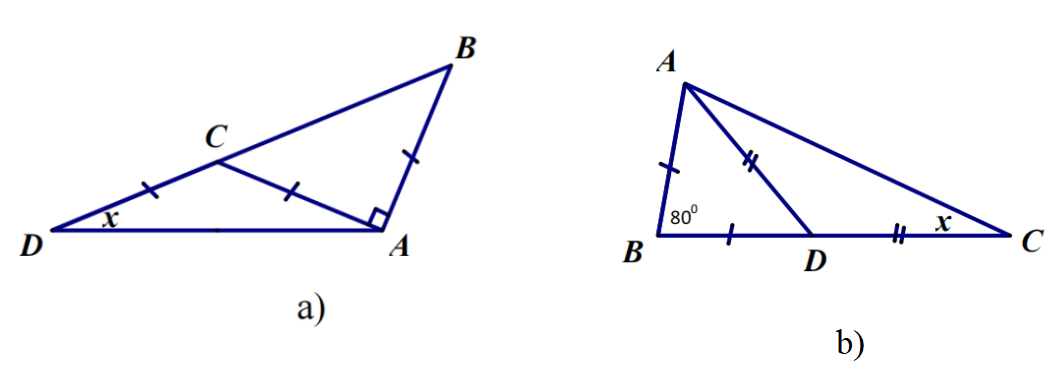
Bài 8: Tìm số đo x trên mỗi hình sau:
Bài 9: Cho ΔABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK. Chứng minh ΔOBC và ΔOHK là các tam giác cân.
Bài 10: Cho điểm M thuộc đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tam giác đều AMC và BMD. Gọi E, F theo thứ tự là trung điểm của AD, CB. Chứng minh: △MEF là tam giác đều.
Hướng dẫn giải:
Bài 1:
|
|
Đúng |
Sai |
|
a) Tam giác cân có một góc 45o là tam giác vuông cân. |
|
x |
|
b) Mỗi góc ngoài của 1 tam giác thì bằng tổng 2 góc không kề nó của tam giác đó. |
x |
|
|
c) Nếu tam giác có 1 cặp cạnh không bằng nhau thì tam giác đó không phải là tam giác cân. |
|
x |
Bài 2: ˆB=ˆC=65o
Bài 3: Đáp án: C
Tam giác ABC cân tại A do AB = AC
Tam giác DEF cân tại D do ˆE=ˆF=64o (tính toán được)
Tam giác GIH không cân do ˆG=58o, ˆI=60o, ˆH=72o
Bài 4: Dễ dàng chứng minh được AE = AF
⇒ΔAEF cân tại A.
Bài 5:
Cách vẽ:
- Vẽ đoạn thẳng BC = 6 cm.
- Vẽ cung tròn tâm C bán kính 6 cm.
- Vẽ cung tròn tâm B bán kính 6 cm.
- Hai cung tròn này cắt nhau tại A.
- Nối AB, AC ta được tam giác ABC cần vẽ.
Bài 6:
a) ΔABD cân
b) ΔABE, ΔACD cân
c) ΔABC, ΔABD, ΔBCD cân
Bài 7:
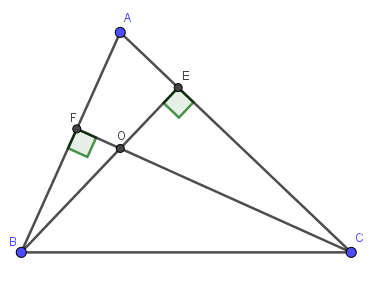
a) Xét ΔAEB và ΔOEC:
^AEB=^BEC=90o
AB=OC (gt)
^ABE=^ECO (vì cùng phụ với góc A)
Do đó: ΔAEB=ΔOEC (g.c.g)
b) Tam giác EBC vuông cân tại E: ^ACB=45o
Bài 8:
a) x = 22,5o
b) x = 25o
Bài 9:
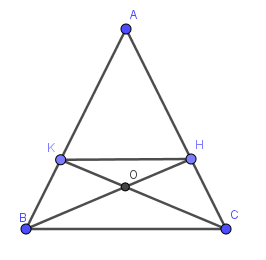
*Tam giác ABC cân tại A ⇒ AB =AC
Mà AH = AK ⇒ BK = HC
Ta chứng minh được ΔBKC= ΔCHB (c.g.c)
⇒^KCB=^HBC
⇒ΔOBC cân tại O.
* Ta có: BH = CK, OB = OC
⇒ OH = OK.
⇒ΔOHKcân tại O.
Bài 10:
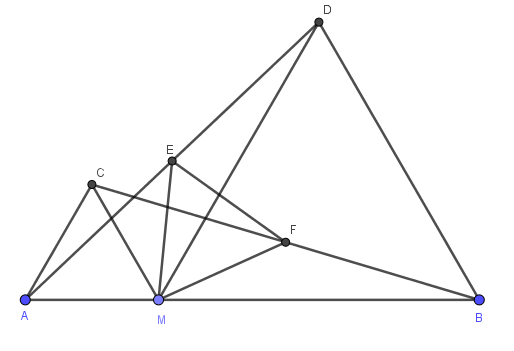
∆AMD =DCMB (c.g.c)
, AD = CB, AE = CF
Có: MAE =MCF (c.g.c)
ME = MF,
Mà cân (do ME = MF)
đều.
Xem thêm các dạng bài tập hay, có đáp án:
50 Bài tập Hình tam giác - Diện tích hình tam giác (có đáp án năm 2024) - Toán lớp 5
60 Bài tập về Tính chất đường phân giác của tam giác (có đáp án năm 2023) - Toán 8
70 Bài tập Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác (có đáp án năm 2024) - Toán 7
70 Bài tập về Sự đồng quy của ba đường phân giác trong một tam giác (có đáp án năm 2024) - Toán 7
50 Bài tập về hình tam giác đều. hình vuông. hình lục giác đều (có đáp án năm 2024) - Toán 6












