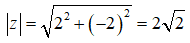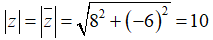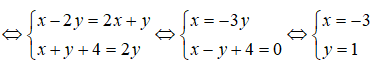Số phức
Kiến thức cần nhớ
1. Số i
Số i là số thỏa mãn: i2 = –1.
2. Định nghĩa số phức
Mỗi biểu thức dạng a + bi , trong đó a; b∈R; i2 = –1 được gọi là một số phức.
Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.
Tập hợp các số phức kí hiệu là C.
Ví dụ 1. Các số sau là những số phức: 2 – 3i; –8 + 4i; 5− i√2; √3 +2i
Ví dụ 2. Số phức 6 – i có phần thực là 6, phần ảo là – 1.
3. Số phức bằng nhau
– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :
a + bi = c + di a = c và b = d.
Ví dụ 3. Tìm các số thực x và y biết :
(2x – 1) + (y – 2)i = 3 + (4 – y)i
Lời giải:
Ta có : (2x – 1) + (y – 2)i = 3 + (4 – y)i
⇔{2x−1= 3y−2= 4−y⇔{x=2y= 3
Vậy x = 2 và y = 3.
– Chú ý :
a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.
Như vậy, mỗi số thực cũng là một số phức. Ta có : R⊂C.
b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi
Đặc biệt : i = 0 + 1.i
Số i được gọi là đơn vị ảo.
Ví dụ 4. Số phức z có phần thực là -12 và phần ảo là 12 là z = −12 + 12i.
4. Biểu diễn hình học số phức
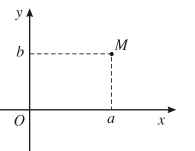
Điểm M(a ; b) trong một hệ tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z = a + bi.
Ví dụ 5.
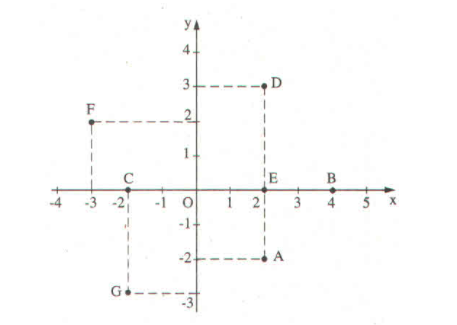
Điểm A biểu diễn số phức 2 – 2i
Điểm B biểu diễn số phức 4.
Điểm C biểu diễn số phức – 2.
Điểm D biểu diễn số phức 2 + 3i.
Điểm E biểu diễn số phức 2.
Điểm F biểu diễn số phức – 3 + 2i.
Điểm G biểu diễn số phức –2 – 3i.
5. Mô đun của số phức
Giả sử số phức z = a + bi được biểu diễn bởi điểm M(a ; b) trên mặt phẳng tọa độ.
Độ dài của vecto →OM được gọi là môđun của số phức z và kí hiệu là |z|.
Vậy |z| = |→OM| hay |a+bi|=|→OM|.
Ta thấy: |a+ bi| = √a2+ b2
Ví dụ 6.
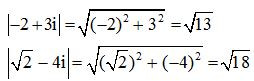
6. Số phức liên hợp
– Định nghĩa : Cho số phức z = a + bi. Ta gọi a – bi là số phức liên hợp của z và kí hiệu là ˉz = a−bi.
Ví dụ 7.
Nếu z = – 3 + 5i thì ˉz = −3− 5i.
Nếu z = – 4 + 4i thì ˉz = −4−4i.
– Nhận xét :
+ Trên mặt phẳng tọa độ các điểm biểu diễn z và ˉz đối xứng nhau qua trục Ox.
+ Từ định nghĩa ta có: ˉˉz = z; |ˉz| = |z|.
Các dạng bài tập về số phức
(Xem thêm trong file pdf)
Dạng 1: Thực hiện các phép toán của số phức, tìm phần thực phần ảo.
Dạng 2. Tìm số phức liên hợp, tính môđun số phức.
Dạng 3. Bài toán liên quan đến điểm biểu diễn số phức.
Dạng 4. Tìm số phức thỏa mãn điều kiện cho trước.
Dạng 5: Bài toán tập hợp điểm biểu diễn số phức.
Bài tập (có hướng dẫn)
1. Bài tập vận dụng
Bài 1: Hai số phức z1 = x - 2i, z22 + yi (x, y ∈ R) là liên hợp của nhau khi
Lời giải:
Ta có z1− = x + 2i. Do đó, hai số phức đã cho gọi là liên hợp của nhau khi và chỉ khi
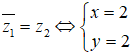
Vậy x= 2, y = 2.
Bài 2: Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là
Lời giải:
Ta có |1 + i| = √(1+1) = √2. Gọi M là điểm biểu diễn của z ta có |z| = OM.
Do đó: |z| = |1 + i| ⇔ OM = √2
Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính R= √2 .
Bài 3: Phần thực của số phức z = -i là
Lời giải:
Ta có: z = -i = 0 - i nên phần thực của số phức z = -i là 0
Bài 4: Phần ảo của số phức z = -1 là
Lời giải:
Ta có: z= -1 = -1 + 0.i nên phần ảo của số phức z = -1 là 0
Bài 5: Số phức liên hợp của số phức z = 1 + i là
Lời giải:
Số phức liên hợp của số phức z = 1 + i là z− = 1 - i
Bài 6: Cho z = 2i -1. Phần thực và phần ảo của z− là
Lời giải:
Ta có z = 2i - 1 = -1 + 2i ⇔ z− = -1 - 2i. Vậy phần thực của z− là -1 và phần ảo của z− là -2.
Bài 7: Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
Lời giải:
Số phức liên hợp của z là z− = 2 + 2i nên khẳng định C là sai.
Bài 8 Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là?
Lời giải:
Ta có z = -1 + 3i => z− = -1 - 3i
Vậy phần thực và phần ảo của z− là -1 và -3.
Bài 9 Môđun của số phức z thỏa mãn z− = 8 - 6i là
Lời giải:
Ta có
Bài 10 Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
Lời giải:
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
Vậy x = -3, y = 1.
Bài 11. Tìm phần thực và phần ảo của số phức z, biết :
a) – 2 + 2i ;
b) 8− i√3;
c) – 8 ;
d) – 10i.
Lời giải :
a) Phần thực là – 2; phần ảo là 2.
b) Phần thực là 8; phần ảo là -√3.
c) Ta có : – 8 = –8 + 0.i nên có phần thực là – 8; phần ảo là 0.
d) Ta có : –10i = 0 – 10i nên có phần thực là 0; phần ảo là –10.
Bài 12. Tìm các số thực x, y biết :
a) (6 – 3x) + (x – y)i = 3 + 2i;
b) (7 – y) + (x – 4)i = (y – 2).i
Lời giải :
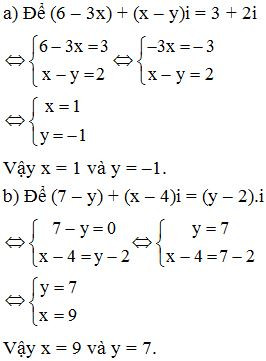
Bài 13. Tính |z|, với :
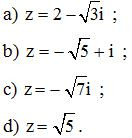
Lời giải :
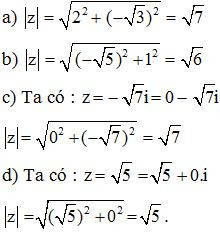
Bài 14. Tìm ˉz, biết :
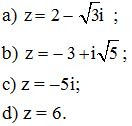
Lời giải:
a) Số phức liên hợp của z là ˉz = 2+ √3i;
b) Số phức liên hợp của z là ˉz= −3− i√5
c) Số phức liên hợp của z là ˉz = 5i;
d) Số phức liên hợp của z là ˉz = 6.
2. Bài tập tự luyện có hướng dẫn
(Xem thêm trong file pdf)
Xem thêm các dạng bài tập liên quan khác:
60 Bài tập về phép chia số phức (có đáp án năm 2023)
60 Bài tập về phương trình bậc hai với hệ số thực ( có đáp án năm 2023 )
60 Bài tập về ứng dụng hình học của tích phân (có đáp án năm 2023)