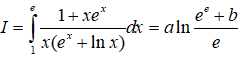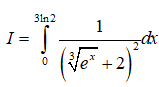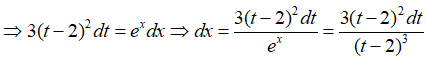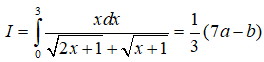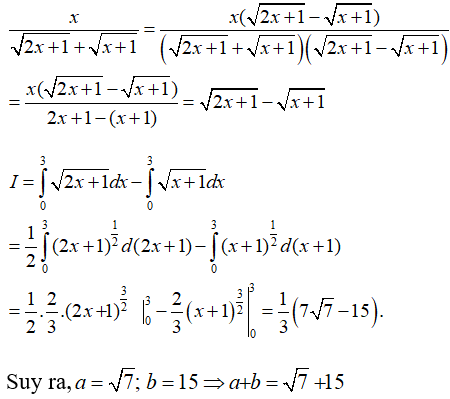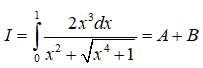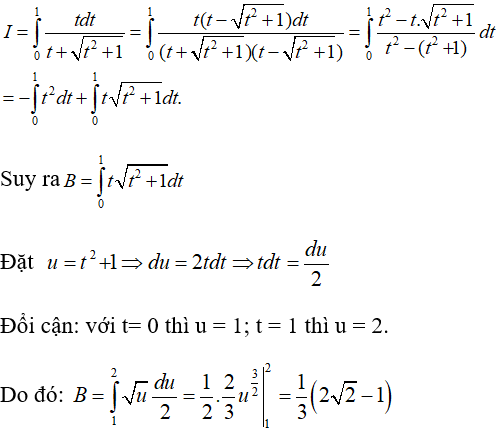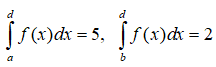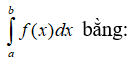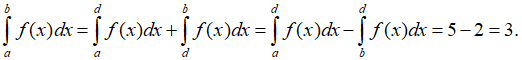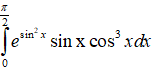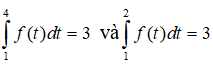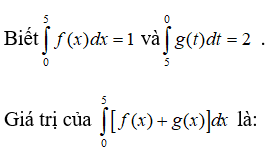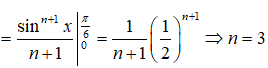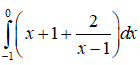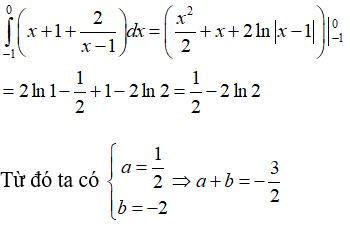60 Bài tập về Tích phân (có đáp án năm 2024) - Toán 12

Kiến thức cần nhớ

I. Khái niệm tích phân

1. Diện tích hình thang cong

- Cho hàm số y = f(x) liên tục, không đổi dấu trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được gọi là hình thang cong.

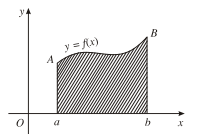
- Ta xét bài toán tìm diện tích hình thang cong bất kì:

Cho hình thang cong giới hạn bởi các đường thẳng x = a; x = b (a < b); trục hoành và đường cong y = f(x),  trong đó f(x) là hàm số liên tục, không âm trên đoạn [a; b].

Với mỗi $x\in \left[a;b\right]$, kí hiệu S(x) là diện tích của phần hình thang cong đó nằm giữa hai đường thẳng vuông góc với Ox lần lượt tại a và b.

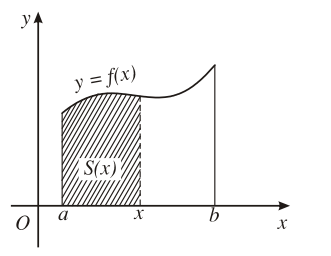
Ta chứng minh được S(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Giả sử F(x) cũng là một nguyên hàm của f(x) thì có một hằng số C sao cho S(x) = F(x) +  C.

Vì S(a) = 0 nên F(a) +  C = 0  hay C =  –  F(a).

Vậy S(x) = F(x) – F(a).

Thay x = b vào đẳng thức trên, ta có diện tích của hình thang cần tìm là:

S(b) = F(b) – F(a).

2. Định nghĩa tích phân

Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn [a; b]) của hàm số f(x), kí hiệu $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$

Ta còn dùng kí hiệu ${\left.F\left(x\right)\right|}_a^b$ để chỉ hiệu số F(b) – F(a).

Vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=$${\left.F\left(x\right)\right|}_a^b=F\left(b\right)-F\left(a\right)$

Ta gọi $\underset{a}{\overset{b}{\int }}$ là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

- Chú ý.

Trong trường hợp a = b hoặc a > b, ta quy ước:

$\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0;$$\underset{a}{\overset{b}{\int }}f\left(x\right)\text{}dx=-\underset{b}{\overset{a}{\int }}f\left(x\right)\text{}dx$

Ví dụ 1.

a) $\underset{0}{\overset{2}{\int }}(x+\text{}2)dx$

$$\begin{gathered} \hspace{0.17em}={\left.\left(\frac{x^2}{2}+2x\right)\right|}_0^2 \\ =6-0=6 \end{gathered}$$

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}(2+\text{\hspace{0.17em}}\cos x)dx$

$$\begin{gathered} ={\left(2x+\text{\hspace{0.17em}\hspace{0.17em}}\sin x\right)}_0^{\frac{\pi }{2}} \\ =(\pi +1)-0 \\ =\pi +1 \end{gathered}$$

- Nhận xét.

a) Tích phân của hàm số f từ a đến b có thể kí hiệu là $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ hay $\underset{a}{\overset{b}{\int }}f\left(t\right)dt$. Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào biến x hay t.

b) Ý nghĩa hình học của tích phân.

Nếu hàm số f(x) liên tục và không âm trên đoạn [a; b] thì tích phân $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ là diện tích S của hình thang cong giới hạn bởi đồ thị của f(x), trục Ox và hai đường thẳng x = a; x = b. Vậy $S\text{\hspace{0.17em}}=\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

II. Tính chất của tích phân.

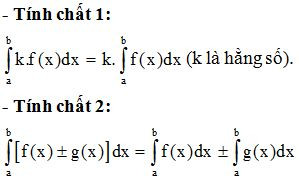
Ví dụ 2. Tính: $\underset{0}{\overset{\pi }{\int }}(3x-4\sin x)dx$.

Lời giải:

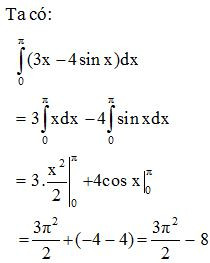
- Tính chất 3.

 $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$$=\underset{a}{\overset{c}{\int }}f\left(x\right)dx+\text{\hspace{0.17em}\hspace{0.17em}}\underset{c}{\overset{b}{\int }}f\left(x\right)dx$ (a < c < b).

Ví dụ 3. Tính $\underset{-2}{\overset{2}{\int }}\left|x\right|dx$.

Lời giải:

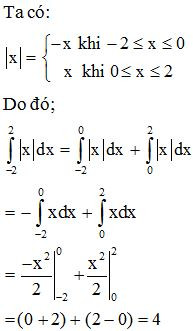
III. Phương pháp tính tích phân

1. Phương pháp đổi biến số

- Định lí:

Cho hàm số f(x) liên tục trên đoạn [a; b]. Giả sử hàm số $x=\phi \left(t\right)$ có đạo hàm liên tục trên đoạn $\left[\alpha ;\beta \right]$ sao cho $\phi \left(\alpha \right)=a;\phi \left(\beta \right)=b$ và $a\le \phi \left(t\right)\le b\forall t\in \left[\alpha ;\beta \right]$.

Khi đó: $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=$$\hspace{0.17em}\underset{\alpha }{\overset{\beta }{\int }}f\left(\phi \left(t\right)\right).\phi \text{'}\left(t\right)dt$

Ví dụ 4.  Tính $\underset{0}{\overset{1}{\int }}\sqrt{1-x^2}dx$.

Lời giải:

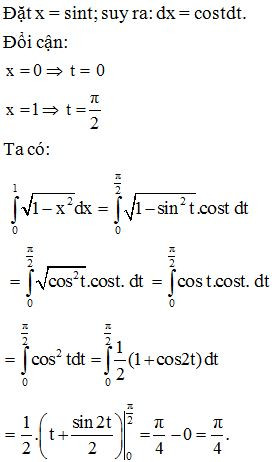
- Chú ý:

Trong nhiều trường hợp ta còn sử dụng phép đổi biến số ở dạng sau:

Cho hàm số f(x) liên tục trên đoạn [a; b]. Để tính $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$, đôi khi ta chọn hàm số u = u(x) làm biến số mới, trong đó trên đoạn [a; b], u(x) có đạo hàm liên tục và $u\left(x\right)\in \left[\alpha ;\beta \right]$.

Giả sử có thể viết: f(x) = g(u(x)). u’(x) với $x\in \left[a;b\right]$ với g(u) liên tục trên đoạn $\left[\alpha ;\beta \right]$

Khi đó, ta có: $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$$=\underset{u\left(a\right)}{\overset{u\left(b\right)}{\int }}g\left(u\right)du$

Ví dụ 5. Tính $\underset{0}{\overset{\sqrt{\pi }}{\int }}x.\sin x^{2}dx$

Lời giải:

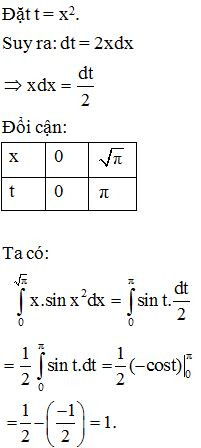
2. Phương pháp tính tích phân từng phần

- Định lí.

Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:

$\underset{a}{\overset{b}{\int }}u\left(x\right).v\text{'}\left(x\right)dx=$${\left.\left[u\left(x\right).v\left(x\right)\right]\right|}_a^b$$-\underset{a}{\overset{b}{\int }}v\left(x\right).u\text{'}\left(x\right)dx$

Hay $\underset{a}{\overset{b}{\int }}udv=u{v}_a^b-\underset{a}{\overset{b}{\int }}vdu$

Ví dụ 6. Tính $I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}x\sin xdx.$

Lời giải:

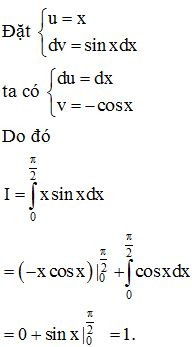
Ví dụ 7. Tính $I=\underset{0}{\overset{e-1}{\int }}x\ln (x+1)dx$.

Lời giải:

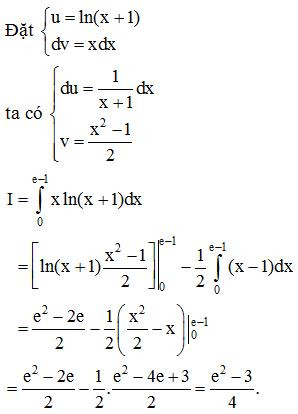
Các dạng bài tập về tích phân

Dạng toán 1. Tính tích phân bằng cách áp dụng định nghĩa, tính chất và bảng nguyên hàm 

Dạng toán 2. Tích phân hàm phân thức hữu tỉ 

Dạng toán 3. Tích phân hàm chứa dấu căn thức 

Dạng toán 4. Tích phân hàm số lượng giác

Dạng toán 5. Tích phân hàm số mũ và hàm số logarit

Bài tập tự luyện

1 Bài tập vận dụng

Câu 1: Cho:

Tính giá trị của a-b.

Lời giải:

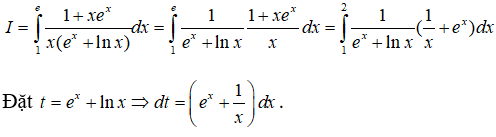
Khi x = 1 thì t = e, khi x = e thì t = e^e + 1 .

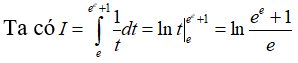
Từ đó suy ra: a = 1; b = 1 nên a – b = 0.

Câu 2: Cho

Giả sử đặt t = $\sqrt[3]{ex}$ + 2 thì ta được:

Lời giải:

 ⇒(t - 2)³ = ex

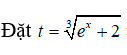
Đổi cận: x = 0 thì t = 3 ; x = 3ln2 thì t = 4

Khi đó

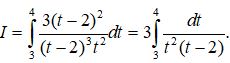
Câu 3: Cho

Khi đó a+b bằng

Lời giải:

Câu 4: Cho

Đặt t = x² . Biết

Lời giải:

Câu 5: Nếu

với a < d < b thì

Lời giải:

Câu 6: Cho tích phân

Nếu biến đổi số t = sin2x thì:

Lời giải:

Ta có

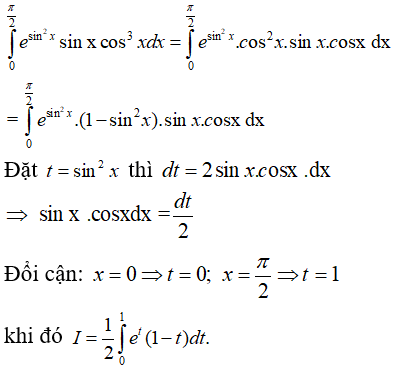
Câu 7: Tính

Lời giải:

Ta có

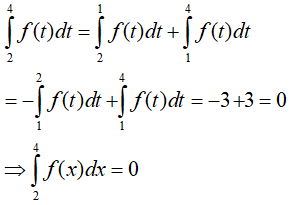
Câu 8:

Lời giải:

Hiển thị đáp án

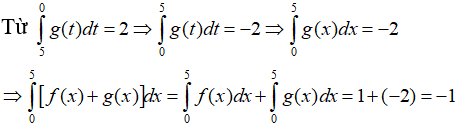
Bài 9:

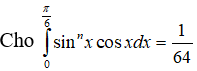
Tìm n?

Lời giải:

Ta có:

 

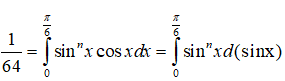
Bài 10: Kết quả của tích phân

được viết dưới dạng a+bln2. Tính giá trị của a+b.

Lời giải:

Ta có:

2 Bài tập tự luyện có đáp án 

Câu 1. $\underset{2}{\overset{4}{\int }}{\left(x+\frac{1}{x}\right)}^{2}dx$  bằng:

A. $\frac{275}{12}$

B. $\frac{305}{16}$

C. $\frac{196}{15}$

D. $\frac{208}{17}$

Câu 2.  $\underset{e-1}{\overset{e^2-1}{\int }}\frac{1}{x+1}dx$  bằng:

A. $3\left(e^2-e\right)$

B. 1

C. $\frac{1}{e^2}-\frac{1}{e}$

D. 2

Câu 3. $\underset{0}{\overset{\ln 2}{\int }}\left(e^x+1\right)e^{x}dx$ bằng:

A. $3\ln 2$

B. $\frac{4}{5}\ln 2$

C. $\frac{5}{2}$

D. $\frac{7}{3}$

Câu 4.  $\underset{0}{\overset{4}{\int }}\frac{1}{\sqrt{2x+1}}dx$  bằng:

A. 5

B. 4

C. 3

D. 2

Câu 5. $\underset{2}{\overset{5}{\int }}{\left(3x-4\right)}^{4}dx$   bằng:

A. $\frac{89720}{27}$

B. $\frac{18927}{20}$

C. $\frac{960025}{18}$

D. $\frac{53673}{5}$

Câu 6. Kết quả của tích phân: $I=\underset{0}{\overset{1}{\int }}\frac{7+6x}{3x+2}dx$

A. $\frac{1}{2}-\ln \frac{5}{2}$

B. $\ln \frac{5}{2}$

C. 2+ $\ln \frac{5}{2}$

D. $3+2\ln \frac{5}{2}$

Câu 7. Tích phân: $\underset{0}{\overset{4}{\int }}\left|x-2\right|dx$

A. 0

B. 2

C. 8

D. 4

Câu 8. Tích phân $\underset{0}{\overset{2}{\int }}\left|x^2-x\right|dx$ bằng

A. $\frac{2}{3}$

B. 0

C. 1

D. $\frac{3}{2}$

Câu 9. Tính $\underset{-1}{\overset{2}{\int }}\frac{dx}{1+\left|1-x\right|}$?

A. 2ln3

B. ln3

C. ln2

D. ln6

Câu 10. Nếu${\int }_1^{4}f\left(x\right)dx=6$  và ${\int }_1^4 g\left(x\right)dx=-5$ thì ${\int }_1^4\left[f\right(x)-g(x\left)\right]$ bằng

A. -1.

B. -11.

C. 1.

D. 11.

Câu 11. Cho biết $\underset{2}{\overset{5}{\int }}f\left(x\right)dx=3$, $\underset{2}{\overset{5}{\int }}g\left(x\right)dx=9$. Giá trị của $A=\underset{2}{\overset{5}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx$ là:

A. Chưa xác định được

B. 12

C. 3

D. 6

Câu 12. Cho $2I={\int }_1^2(2x^3+\ln x)dx$. Tìm I?

A. $1+2\ln 2$

B. $\frac{13}{2}+2\ln 2$

C. $\frac{13}{4}+\ln 2$

D. $\frac{1}{2}+\ln 2$

Câu 13. Nếu $\underset{0}{\overset{10}{\int }}f\left(x\right)dx=17$ và $\underset{0}{\overset{8}{\int }}f\left(x\right)dx=12$ thì $\underset{8}{\overset{10}{\int }}f\left(x\right)dx$ bằng:

A. 5

B. 29

C. - 5

D. 15

Câu 14. f và g là hai hàm số theo x. Biết rằng $\forall x\in [a,b],f\text{'}\left(x\right)=g\text{'}\left(x\right)$

Trong các mệnh đề:

(I) $\forall x\in [a,b],f\text{'}\left(x\right)=g\left(x\right)$

(II) $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{b}{\int }}g\left(x\right)dx$

(III) $\forall x\in [a;b],f\left(x\right)-f\left(a\right)=g\left(x\right)-g\left(a\right)$

Mệnh đề nào đúng?

A. I

B. II

C. Không có

D. III

Câu 15. Để $\underset{1}{\overset{k}{\int }}\left(k-4x\right)dx+3k+1=0$ thì giá trị của k là bao nhiêu ?

A. 1

B. 3

C. 2

D. 4

Câu 16. Nếu $\underset{0}{\overset{6}{\int }}f\left(x\right)dx=10$ và $\underset{0}{\overset{4}{\int }}f\left(x\right)dx=7$, thì $\underset{4}{\overset{6}{\int }}f\left(x\right)dx$ bằng:

A. 3

B. 17

C. 170

D. - 3

Câu 17. Tìm a sao cho $I=\underset{1}{\overset{2}{\int }}{\text{[a}}^{\text{2}}{\text{+(4 - a)x + 4x}}^{\text{3}}\text{]dx = 12}$

A. Đáp án khác

B. a = - 3

C. a = 5

D. a = 3

Câu 18. Biết $\underset{0}{\overset{b}{\int }}\left(2x-4\right)dx=0$, khi đó b nhận giá trị bằng:

A. $b=1$  hoặc $b=4$

B. $b=0$  hoặc $b=2$

C. $b=1$  hoặc $b=2$

D. $b=0$  hoặc $b=4$

Câu 19. Cho $\underset{0}{\overset{1}{\int }}{e}^{3x}dx=\frac{e^a-1}{b}$. Khi đó khẳng định nào sau đây là đúng

A. a = - b

B. a < b

C. a > b

D. a = b

Câu 20. Nếu $\underset{a}{\overset{d}{\int }}f\left(x\right)dx=5$; $\underset{b}{\overset{d}{\int }}f\left(x\right)dx=2$, với $a<d<b$ thì $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ bằng:

A. - 2

B. 3

C. 8

D. 0

Câu 21. Cho tích phân $I=\underset{0}{\overset{3}{\int }}\left|2^x-4\right|dx$, trong các kết quả sau:

(I). $I=\underset{2}{\overset{3}{\int }}\left(2^x-4\right)dx+\underset{0}{\overset{2}{\int }}\left(2^x-4\right)dx$

(II). $I=\underset{2}{\overset{3}{\int }}\left(2^x-4\right)dx-\underset{0}{\overset{2}{\int }}\left(2^x-4\right)dx$

(III). $I=2\underset{2}{\overset{3}{\int }}\left(2^x-4\right)dx$

Kết quả nào đúng?

A. Chỉ II.

B. Chỉ III

C. Cả I, II, III.

D. Chỉ I.

Câu 22. Cho hàm số y = f(x) liên tục và chỉ triệt tiêu khi x = c trên [a; b]. Các kết quả sau, câu nào đúng?

A. $\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx\ge \left|\underset{a}{\overset{b}{\int }}f\left(x\right)dx\right|$

B. $\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx=\underset{a}{\overset{c}{\int }}\left|f\left(x\right)\right|dx+\underset{c}{\overset{b}{\int }}\left|f\left(x\right)\right|dx$

C. $\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|dx=\left|\underset{a}{\overset{c}{\int }}\left|f\left(x\right)\right|dx\right|+\left|\underset{a}{\overset{b}{\int }}f\left(x\right)dx\right|$

D. A, B, C đều đúng

Câu 23. Khẳng định nào sau đây sai về kết quả $\underset{-1}{\overset{0}{\int }}\left|\frac{x+1}{x-2}\right|dx=a\ln \frac{b}{c}-1$ ?

A.  $a.b=3(c+1)$

B. $ac=b+3$

C. $a+b+2c=10$

D. $ab=c+1$

Câu 24. Cho f(x) là hàm số chẵn và liên tục trên R thỏa mãn $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=2$. Khi đó giá trị tích phân $\underset{0}{\overset{1}{\int }}f\left(x\right)dx$ là:

A. 2

B. 1

C. $\frac{1}{2}$

D. $\frac{1}{4}$

Câu 25. Cho hàm số f liên tục trên đoạn [a; b] có một nguyên hàm là hàm F trên đoạn [a; b]. Trong các phát biểu sau, phát biểu nào sai ?

A. $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=F\left(b\right)-F\left(a\right)$

B. $F\text{'}\left(x\right)=f\left(x\right)$ với mọi $x\in (a;b)$.     

C. $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=f\left(b\right)-f\left(a\right)$.

D. Hàm số G cho bởi $G\left(x\right)=F\left(x\right)+5$ cũng thỏa mãn $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=G\left(b\right)-G\left(a\right)$.

Câu 26. Cho hai hàm số f và g liên tục trên đoạn [a; b] sao cho $g\left(x\right)\ne 0$ với mọi $x\in [a;b]$. Xét các khẳng định sau:

I. $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx+\underset{a}{\overset{b}{\int }}g\left(x\right)dx$.

II. $\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx-\underset{a}{\overset{b}{\int }}g\left(x\right)dx$.

III. $\underset{a}{\overset{b}{\int }}\left[f\left(x\right).g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx.\underset{a}{\overset{b}{\int }}g\left(x\right)dx$.

IV. $\underset{a}{\overset{b}{\int }}\frac{f\left(x\right)}{g\left(x\right)}dx=\frac{{\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}}{{\displaystyle \underset{a}{\overset{b}{\int }}g\left(x\right)dx}}$.

Trong các khẳng định trên, có bao nhiêu khẳng định sai?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 27. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu f là hàm số chẵn trên R thì $\underset{0}{\overset{1}{\int }}f\left(x\right)dx=\underset{-1}{\overset{0}{\int }}f\left(x\right)dx$.

B. Nếu $\underset{-1}{\overset{0}{\int }}f\left(x\right)dx=\underset{0}{\overset{1}{\int }}f\left(x\right)dx$ thì f là hàm số chẵn trên đoạn $[-1;1]$ 

C. Nếu $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=0$ thì f là hàm số lẻ trên đoạn $[-1;1]$

D. Nếu $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=0$ thì f là hàm số chẵn trên đoạn $[-1;1]$

Câu 28. Tích phân $\underset{0}{\overset{2}{\int }}k{e}^{x}dx$ (với k là hằng số )có giá trị bằng:

A. $k(e^2-1)$

B. $e^2-1$

C. $k(e^2-e)$

D. $e^2-e$

Câu 29. Tích phân $\underset{-1}{\overset{5}{\int }}\left|x^2-2x-3\right|dx$ có giá trị bằng

A. 0

B. $\frac{64}{3}$

C. 7.

D. 12,5.

Câu 30. Giá trị của a để đẳng thức $\underset{1}{\overset{2}{\int }}\left[a^2+(4-4a)x+4x^3\right]dx=\underset{2}{\overset{4}{\int }}2xdx$ là đẳng thức đúng

A. 4.

B. 3.

C. 5

D. 6.

Đáp án

Xem thêm các dạng bài tập toán hay khác:

60 Bài tập về ứng dụng hình học của tích phân (có đáp án năm 2023) - Toán 12

60 Bài tập về Nguyên hàm ( có đáp án năm 2023 ) - Toán 12

60 Bài tập về số phức (có đáp án năm 2023) - Toán 12

60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024) có đáp án - Toán 12

60 Bài tập về Hàm số mũ, Hàm số logarit (2024) có đáp án - Toán 12