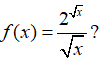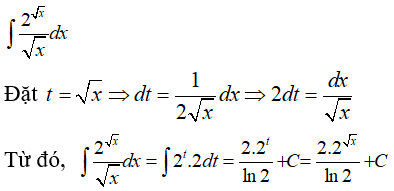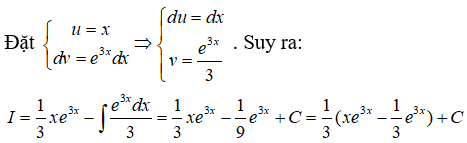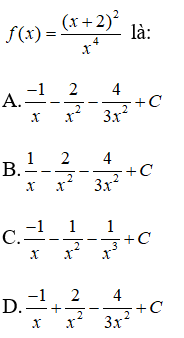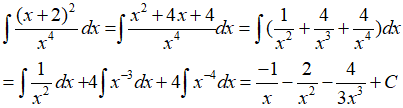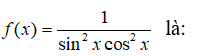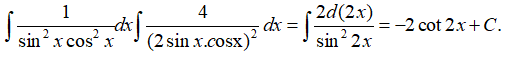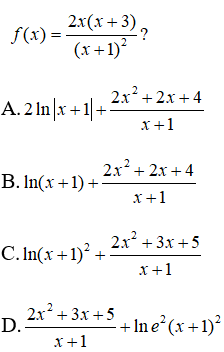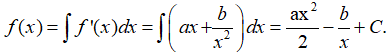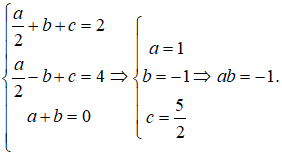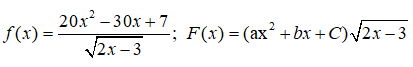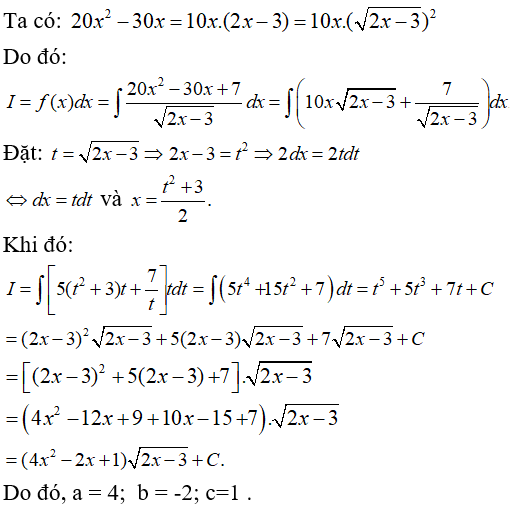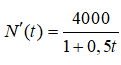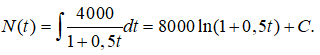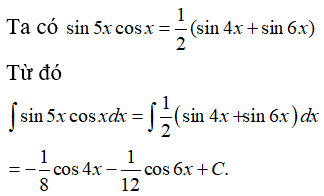60 Bài tập về Nguyên hàm ( có đáp án năm 2024 )

Tổng hợp các dạng bài tập về Nguyên hàm

Kiến thức cơ bản

1. Nguyên hàm

- Định nghĩa

Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng của R). 

Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi $x\in K$.

Ví dụ 1.

- Hàm số F(x) = sinx + 6 là một nguyên hàm của hàm số f(x) = cosx trên khoảng $\left(-\infty ;+\infty \right)$ vì F’(x) = (sinx + 6)’ = cosx với $\forall x\in \left(-\infty ;+\infty \right)$

- Hàm số $F\left(x\right)=\frac{x+\text{\hspace{0.17em}}2}{x-3}$là một nguyên hàm của hàm số $f\left(x\right)=\frac{-5}{{(x-3)}^2}$ trên khoảng $(-\infty ;3)\cup (3;+\text{\hspace{0.17em}}\infty )$

Vì $F\text{'}\left(x\right)={\left(\frac{x+\text{\hspace{0.17em}}2}{x-3}\right)}^{\text{'}}$$=\frac{-5}{{(x-3)}^2}=f\left(x\right)$ với $\forall x\in (-\infty ;3)\cup (3;+\infty )$.

- Định lí 1.

 Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.

- Định lí 2.

Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.

Do đó $F\left(x\right)+C;C\in ℝ$ là họ tất cả các nguyên hàm của f(x) trên K.

Kí hiệu: $\underset{}{\overset{}{\int }}f\left(x\right)dx=F\left(x\right)+C$

- Chú ý: Biểu thức f(x)dx chính là vi phân của nguyên hàm F(x) của f(x), vì dF(x) = F’(x)dx = f(x)dx.

Ví dụ 2.

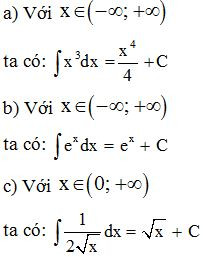
2. Tính chất của nguyên hàm

- Tính chất 1.

$\int f\text{'}\left(x\right)dx=f\left(x\right)\text{\hspace{0.17em}\hspace{0.17em}}+C$

Ví dụ 3.

$\int \left(\text{}{4}^x\right)\text{'}dx$$\hspace{0.17em}=\int 4^x.\ln 4.dx=4^x+C$

- Tính chất 2.

$\int kf\left(x\right)\text{}dx=k.\int f\left(x\right)\text{}dx$(k là hằng số khác 0).

- Tính chất 3.

$\int \left[f\left(x\right)\pm g\left(x\right)\right]dx$$=\int f\left(x\right)dx\pm \int g\left(x\right)dx$

Ví dụ 4. Tìm nguyên hàm của hàm số $f\left(x\right)=3x^2+\text{\hspace{0.17em}\hspace{0.17em}}2\sin x$ trên khoảng $\left(-\infty ;+\text{\hspace{0.17em}}\infty \right)$.

Lời giải:

Với $x\in \left(-\infty ;+\text{\hspace{0.17em}}\infty \right)$ ta có:

$\begin{array}{l}\int (3x^2+2\sin x)dx\\ =\int 3x^{2}dx+2\int \sin xdx\\ =x^3+\text{\hspace{0.17em}}2.(-c\text{osx) +\hspace{0.17em}\hspace{0.17em}C }\\ = \hspace{0.17em}\hspace{0.17em}{x}^3-2c\text{osx +\hspace{0.17em}\hspace{0.17em}C}\end{array}$

3. Sự tồn tại nguyên hàm

Định lí:

Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

Ví dụ 5.

a) Hàm số $y=\sqrt{x}$ có nguyên hàm trên khoảng $\left(0;+\infty \right)$.

$$\begin{gathered} \int \sqrt{x}dx=\int x^{\frac{1}{2}}dx \\ =\frac{2}{3}{x}^{\frac{3}{2}}+C \\ =\frac{2}{3}x\sqrt{x}+\text{\hspace{0.17em}\hspace{0.17em}}C \end{gathered}$$

b) Hàm số y = $\frac{1}{x}$ có nguyên hàm trên khoảng $\left(-\infty ;0\right)\cup \left(0;+\infty \right)$

$\int \frac{1}{x}dx=\ln \left|x\right|+\text{\hspace{0.17em}\hspace{0.17em}}C$

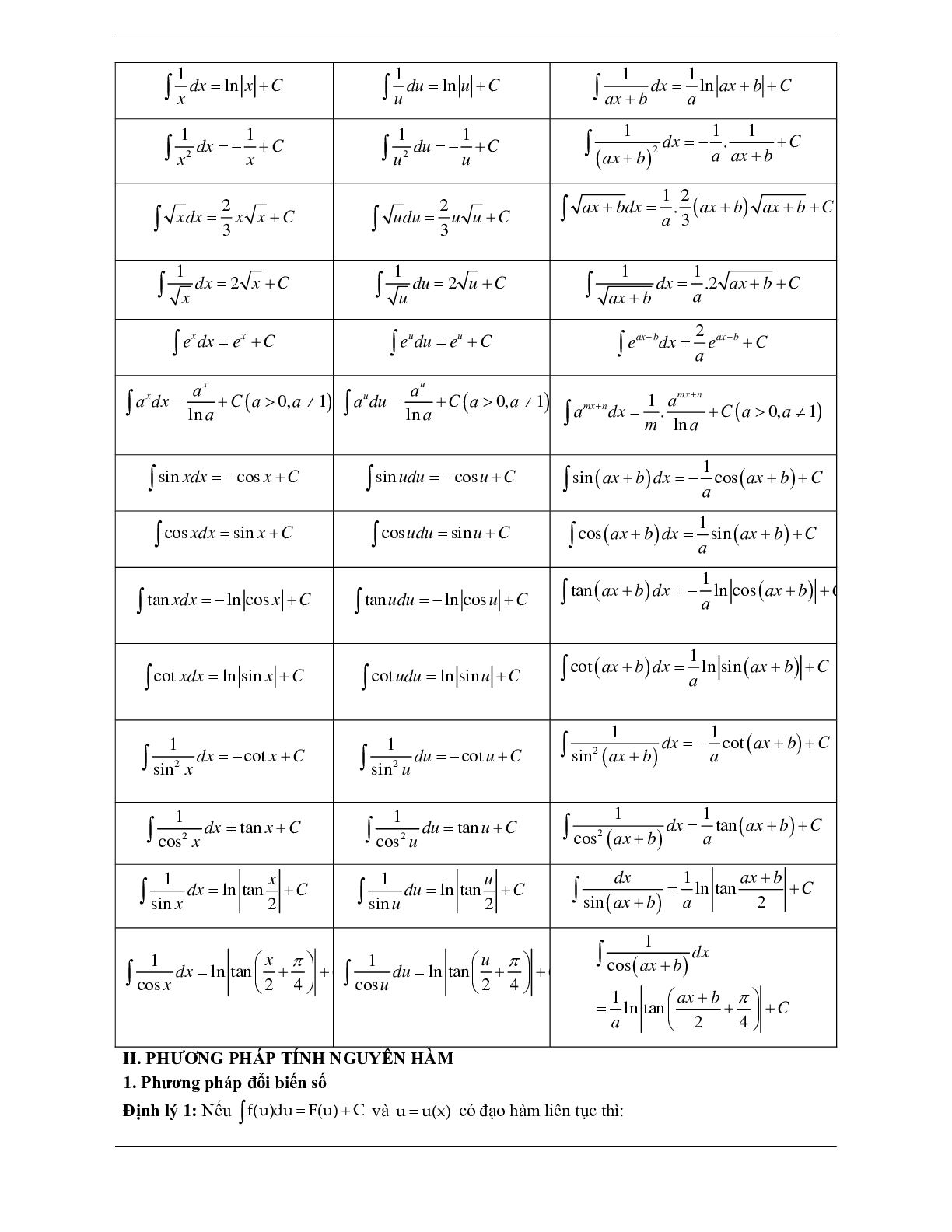
4. Bảng nguyên hàm của một số hàm số thường gặp

Ví dụ 6. Tính:

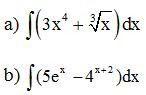
Lời giải:

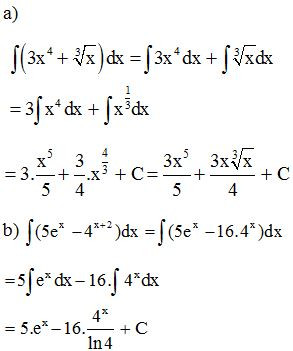
- Chú ý: Từ đây, yêu cầu tìm nguyên hàm của một hàm số được hiểu là tìm nguyên hàm trên từng khoảng xác định của nó.

Phương pháp tính nguyên hàm

1. Phương pháp đổi biến số

- Định lí 1.

Nếu $\int f\left(u\right)du=F\left(u\right)+\text{\hspace{0.17em}\hspace{0.17em}}C$ và u = u(x) là hàm số có đạo hàm liên tục thì:

$\int f\left(u\right(x\left)\right).u\text{'}\left(x\right)dx$$=F\left(u\right(x\left)\right)+\text{\hspace{0.17em}\hspace{0.17em}}C$

Hệ quả: Nếu u = ax + b (a ≠ 0), ta có:

$\int f(ax+\text{\hspace{0.17em}}b)dx$$\hspace{0.17em}=\frac{1}{a}F(ax+\text{\hspace{0.17em}}b)+\text{\hspace{0.17em}}C$

Ví dụ 7. Tính $\int {(3x+\text{\hspace{0.17em}}2)}^{3}dx$.

Lời giải:

Ta có: $\int u^{3}du=\frac{u^4}{4}+\text{\hspace{0.17em}}C$ nên theo hệ quả ta có:

$\int {(3x+\text{\hspace{0.17em}}2)}^{3}dx$$\hspace{0.17em}=\frac{{(3x+2)}^4}{4}+\text{\hspace{0.17em}\hspace{0.17em}}C$

Chú ý:

Nếu tính nguyên hàm theo biến mới u (u = u(x)) thì sau khi tính nguyên hàm, ta phải trở lại biến x ban đầu bằng cách thay u bởi u(x).

Ví dụ 8. Tính $\int \sin x.c{\text{os}}^{2}xdx$

Lời giải:

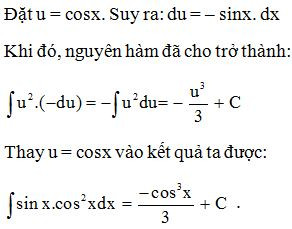
2. Phương pháp tính nguyên hàm từng phần

- Định lí 2.

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:

$\int u\left(x\right).v\text{'}\left(x\right).dx$$\hspace{0.17em}=u\left(x\right).v\left(x\right)-\int u\text{'}\left(x\right).v\left(x\right)dx$

- Chú ý.

Vì u’(x) dx = du; v’(x) dx = dv. Nên đẳng thức trên còn được viết ở dạng:

$\int udv=uv-\int vdu$

Đó là công thức nguyên hàm từng phần.

Ví dụ 9. Tính

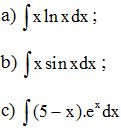
Lời giải:

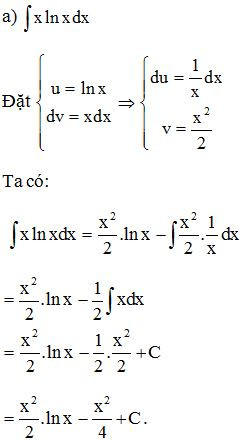
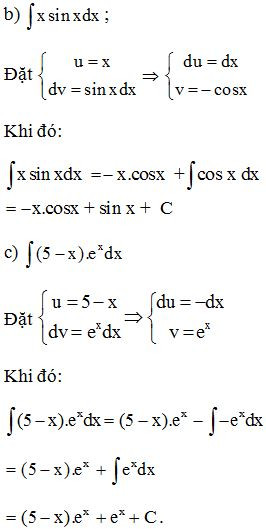
Các dạng bài tập về nguyên hàm

(Xem thêm trong file pdf)

Dạng 1: Tìm nguyên hàm bằng các phép biến đổi sơ cấp.

Dạng 2: Phương pháp đổi biến dạng 1, đặt u = u(x).

Dạng 3: Tìm nguyên hàm bằng cách đổi biến dạng 2.

Dạng 4: Tìm nguyên hàm bằng phương pháp nguyên hàm từng phần.

Dạng 5: Các bài toán thực tế ứng dụng nguyên hàm.

Bài tập có hướng dẫn

1. Bài tập vận dụng

2. Bài tập tự luyện có hướng dẫn

(Xem thêm trong file pdf)

Xem thêm các dạng bài tập liên quan khác:

Lý thuyết Nguyên hàm từng phần và các dạng bài tập (có đáp án) chi tiết nhất 2024

60 Bài tập về Tích phân (có đáp án năm 2024)

60 Bài tập về ứng dụng hình học của tích phân (có đáp án năm 2023)

60 Bài tập về số phức (có đáp án năm 2023)

60 Bài tập về phép chia số phức (có đáp án năm 2023)