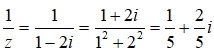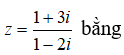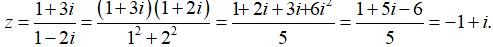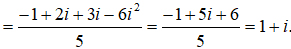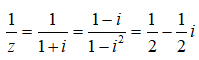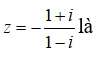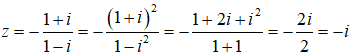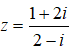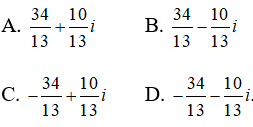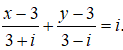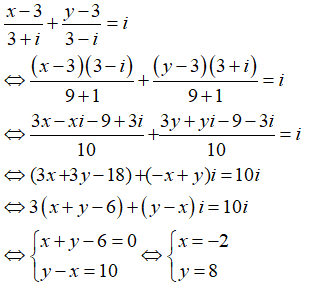60 Bài tập về phép chia số phức (có đáp án năm 2023) - Toán 12

Kiến thức cần nhớ

1. Tổng và tích của hai số phức liên hợp

Cho số phức z = a + bi, ta có:

$z+\text{\hspace{0.17em}\hspace{0.17em}}\overline{z}$= (a + bi) + (a – bi) = 2a;

$z.\text{\hspace{0.17em}\hspace{0.17em}}\overline{z}$ = (a + bi). (a – bi) = a² – (bi)² = a² + b² =${\left|z\right|}^2$

Do đó:

+ Tổng của một số phức với số phức liên hợp của nó bằng hai lần phần thực của số phức đó.

+ Tích của một số phức với số phức liên hợp của nó bằng bình phương môđun của số phức đó.

Vậy tổng và tích của hai số phức liên hợp là một số thực.

2. Phép chia hai số phức

Chia số phức c + di cho số phức a + bi khác 0 là tìm số phức z sao cho

 c + di = (a + bi).z. Số phức z được gọi là thương trong phép chia c + di cho a + bi và kí hiệu là: $z=\frac{c+di}{a+\text{\hspace{0.17em}\hspace{0.17em}}bi}$.

Ví dụ 1. Thực hiện phép chia 4 – 6i cho 1 + i.

Lời giải:

Giả sử $z=\frac{4-6i}{1+i}$

Theo định nghĩa ta có: (1 + i).z = 4 – 6i.

Nhân cả hai vế với số phức liên hợp của 1 + i ta được:

(1 – i) .(1 + i).z = (1 – i).(4 – 6i)

Suy ra: 2z = – 2 – 10i

Do đó, z = –1 – 5i

Vậy $\frac{4-6i}{1+\text{}i}=-1-5i$.

– Tổng quát:

Giả sử $z=\frac{c+di}{a+bi}$. Theo định nghĩa phép chia số phức, ta có:

(a + bi).z = c + di

Nhân cả hai vế với số phức liên hợp của a + bi, ta được:

(a – bi)(a + bi).z = (a – bi)(c + di)

Hay (a² + b²).z = (ac + bd) + (ad – bc).i

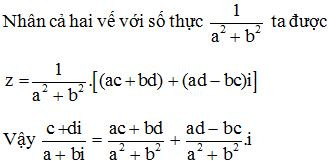
– Chú ý. Trong thực hành để tính thương $\frac{c+\text{}di}{a+bi}$, ta nhân cả tử và mẫu với số phức liên hợp của a + bi.

Ví dụ 2. Thực hiện phép chia 2 – 4i cho 2 + i.

Lời giải:

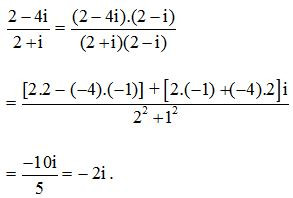
Các dạng bài tập về phép chia số phức

Bài tập tự luyện

1 Bài tập vận dụng

Bài 1: Cho số phức z thỏa mãn (2 + 3i)z = 1 Khi đó, $\overline{z}$ + 2z bằng

Lời giải:

Ta có: (2 + 3i)z = 1 - 5i. Do đó

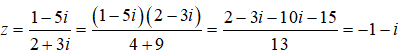
⇒ z− = -1 + i

Bài 2: Nghịch đảo của số phức z = 1 - 2i là?

Lời giải:

Ta có

Bài 3: Số phức

Lời giải:

Ta có

Câu 4: Số phức z thỏa mãn z(1 + 2i) + 1 - i = 2i là

Lời giải:

Ta có:z(1 + 2i) + 1 - i = 2i là <=> z(1 + 2i) = -1 + 3i

Do đó:

 

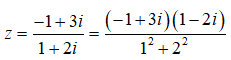
Câu 5: Nghịch đảo của số phức z = 1 + i là?

Lời giải:

Nghịch đảo của số phức z = 1 + i là

Câu 6: Phần thực và phần ảo của số phức

Lời giải:

Ta có

Vậy phần thực và phần ảo của z là 0 và -1

Câu 7: Cho số phức

Phần thực và phần ảo của số phức w = (z + 1)(z + 2) là

Lời giải:

Ta có

Suy ra w = (z + 1)(z + 2) = (i + 1)(i + 2) = -1 + 2i + i + 2 = 1 + 3i

Vậy phần thực và phần ảo của w là 1 và 3

Câu 8: Số phức

 

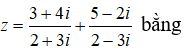
Lời giải:

Ta có

Câu 9: Cho số phức z thỏa mãn (2 + 3i)z = 1 Khi đó, z− + 2z bằng

Lời giải:

Ta có: (2 + 3i)z = 1 - 5i. Do đó

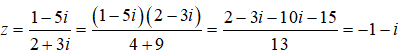
⇒ z− = -1 + i

Câu 10: Các số thực x, y thỏa mãn

Khi đó, tổng T = x + y bằng?

Lời giải:

Ta có

Vậy T = -2 + 8 = 6

2 Bài tập tự luyện có hướng dẫn