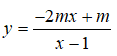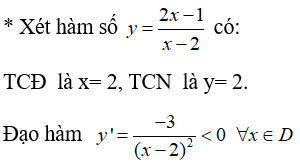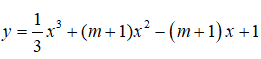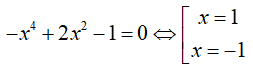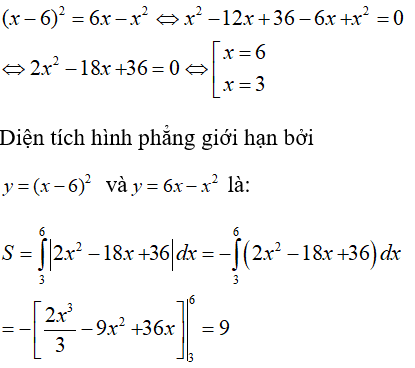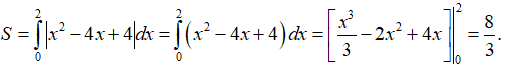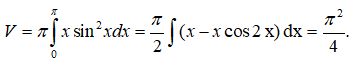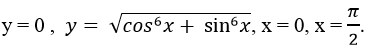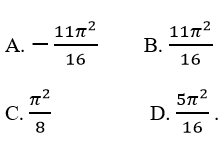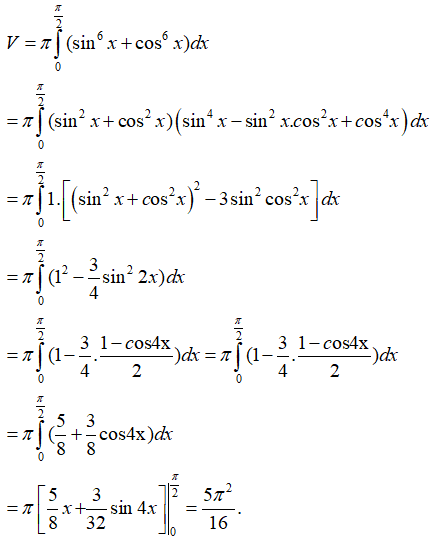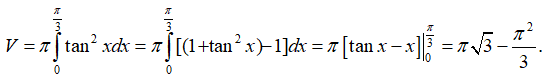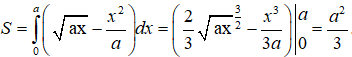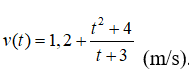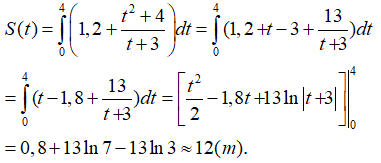Cách tự học môn Toán 12 (2024) chi tiết nhất

Cách tự học môn Toán 12

I. Lý thuyết 

1. Chuẩn bị tài liệu cần thiết để tự học Toán ôn thi đại học

Khi bắt đầu học bất cứ một môn học gì chúng ta đều cần chuẩn bị những tài liệu học tập và không thể thiếu để phục vụ cho việc học đó. Học Toán hay học một môn học nào khác cũng đều như vậy. Riêng với môn Toán, những tài liệu cần thiết và không thể nào thiếu được cho người bắt đầu và tự học toán ôn thi đại học bao gồm:

• Tài liệu: Bao gồm có sách giáo khoa, sách bài tập và sách tham khảo. Đây là tài liệu không thể thiếu khi học sinh bắt đầu tự học Toán.
  • Sách giáo khoa: giúp định hướng chuẩn nhất các kiến thức cơ bản về lý thuyết. Bài tập sẽ xuất hiện trong nội dung bài thi THPT QG.
  • Sách tham khảo: giúp hệ thống lại đầy đủ các dạng bài tập từ cơ bản đến nâng cao. Trang bị kĩ năng cần thiết để làm tốt các dạng bài trắc nghiệm toán không có trong SGK.
• Ngoài ra, nên tham gia các hội nhóm hoặc fanpage luyện thi chuyên Toán. Trên đây thường sẽ cập nhật tài liệu ôn tập cần thiết cho môn Toán nhanh và đa dạng.

2. Xác định kiến thức trọng tâm 

Khóa thi THPT Quốc Gia năm 2016 – 2017, việc tự học là vô cùng dễ dàng bởi vì đây là năm đầu tiên mà Bộ Giáo Dục đổi mới phương án thi. Kiến thức thi đại học môn Toán tập trung chính ở chương trình học của lớp 12.

Từ năm 2018, nội dung có trong bài thi Toán sẽ được mở rộng cả chương trình học toán 11. Vì vậy, các em cần nắm được đâu là kiến thức trọng tâm, đâu là kiến thức bổ sung?

Với riêng môn Toán, trong chương trình lớp 11 và lớp 12, các em sẽ cần phải nắm được những kiến thức trọng tâm sau:

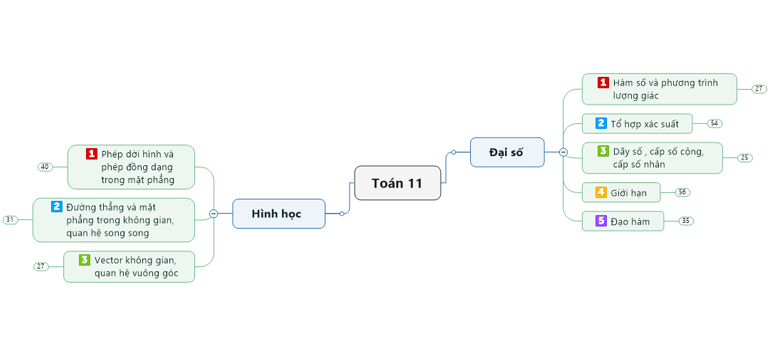
2.1. Chương trình Toán lớp 11: 

• Đại số: Hàm số lượng giác và phương trình lượng giác; Các bài toán tổ hợp; Ôn tập phần giới hạn của hàm số; Đạo hàm.

• Hình học: Tự học phần phép dời hình, đồng dạng trong một mặt phẳng; Đường thẳng mặt phẳng và quan hệ song song; Vecto trong không gian và quan hệ vuông góc trong không gian

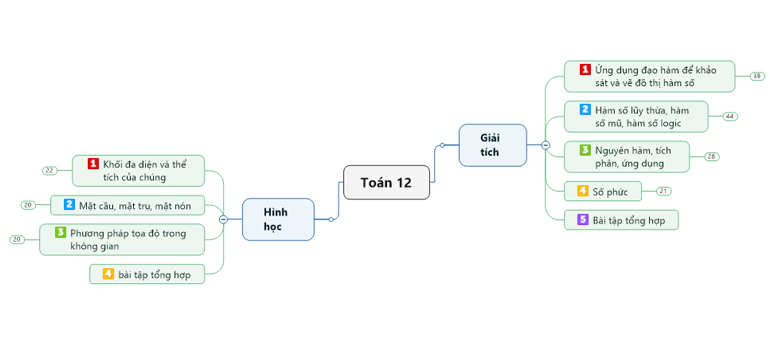
2.2. Chương trình Toán lớp 12: 

• Đại số: Ứng dụng đạo hàm để khảo sát, vẽ đồ thị hàm số; Dạng bài hàm số mũ, logarit; Nguyên hàm và tích phân; Số phức. 

• Hình học: Khối đa diện; ôn tập kiến thức về mặt nón, mặt trụ, mặt cầu và phương pháp tọa độ trong không gian. 

3. Tự luyện thi bằng cách học theo chuyên đề

Nếu như có điều kiện để đi học thêm, giáo viên sẽ bồi dưỡng chuyên sâu và theo dõi sát sao sự tiến bộ của các em.

Tuy nhiên, nếu như tự học ở nhà với những tài liệu đã được chuẩn bị thì bạn cần học theo sát những định hướng của sách giáo khoa. Luyện đề bằng các bài tập theo sách tự ôn, sách bài tập, đề từ các năm trước.

 Các bạn học sinh sẽ cần học những gì?

• Cần phải học và nắm thật chắc những kiến thức lý thuyết của mỗi chuyên đề Toán học
• Làm nhuần nhuyễn từng dạng bài tập nhỏ nhất của từng chuyên đề
• Luyện tập nhiều các dạng bài tập của từng chuyên đề đó từ dễ đến khó.

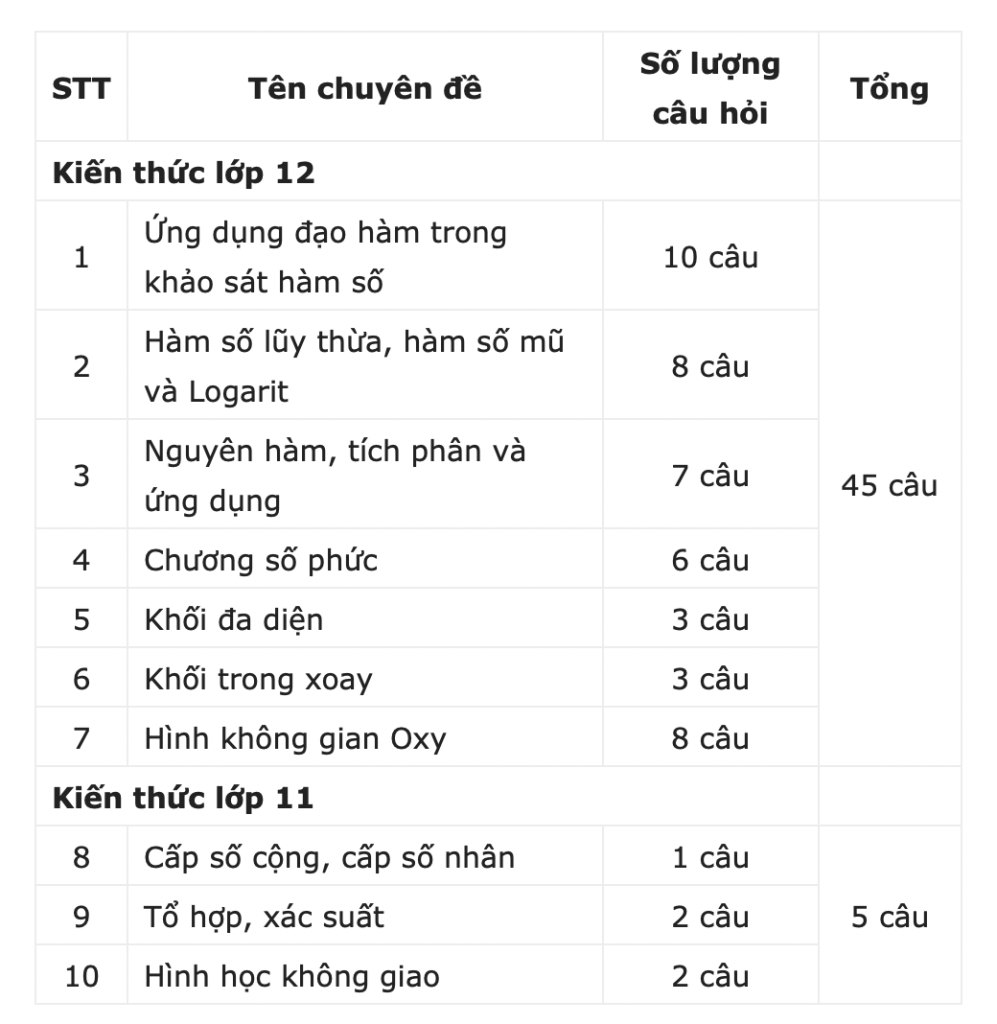
4. Tổng ôn tập sau khi đã học xong các chuyên đề

Học nhuần nhuyễn các kiến thức cơ bản, sau đó là tổng ôn tập và luyện đề.

Đối với những trường hợp chỉ cần đủ điểm để tốt nghiệp THPT thì các em nên tập trung vào những dạng toán cơ bản. Không nên tập trung vào làm đề toán nâng cao, ôn tập trọng tâm để lấy điểm 5 – 6 như: 

• Phần hàm số lượng giác và phương trình lượng giác
• Các dạng toán tổ hợp
• Phần giới hạn của hàm số
• Các ứng dụng của đạo hàm để vẽ, khảo sát đồ thị hàm số
• Ôn tập hàm số mũ và logarit
• Tập trung vào một vài bài toán tính tọa độ không gian

II. Bài tập vận dụng

Bài 1: Cho hàm số y = x² - 2|x| + 2 và các mệnh đề

(1) Hàm số trên liên tục trên R

(2) Hàm số trên có đạo hàm tại x = 0

(3) Hàm số trên đạt GTNN tại x = 0.

(4) Hàm số trên đạt GTLN tại x = 0.

(5) Hàm số trên là hàm chẵn

(6) Hàm số trên cắt trục hoành tại duy nhất một điểm

Trong các mệnh đề trên, số mệnh đề đúng là

Lời giải:

* Hàm số đã cho liên tục trên R vì với 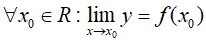 nên (1) đúng

* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.

*y = x² - 2|x| + 2 = |x|² - 2|x| + 2 = (|x| - 1)2 + 1 ≥ 1 ∀ x

Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1

nên hàm số không có GTLN.

* Phương trình x² - 2|x| + 2=0 vô nghiệm nên đồ thị không cắt trục hoành.

f(-x)=(-x)² - 2|-x| + 2 = x² - 2|x| + 2 = f(x)

Nên hàm số đã cho là hàm số chẵn.

Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.

Bài 2: Hàm số

đồng biến trên từng khoảng xác định của nó khi:

Lời giải:

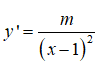
Để hàm số tăng trên từng khoảng xác định thì y’ > 0 <=> m > 0.

Bài 3: Trong các tiếp tuyến tại các điểm trên đồ thị hàm số y = x³ - 3x² + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng:

Lời giải:

Tiếp tuyến của đồ thị hàm số có hệ số góc là

k = y' = 3x² - 6x = (3x² - 6x + 3) - 3 = 3(x - 1)² - 3 ≥ -3 ∀x ∈ R

Trong các tiếp tuyến tại các điểm trên đồ thị hàm số, tiếp tuyến có hệ số góc nhỏ nhất bằng -3.

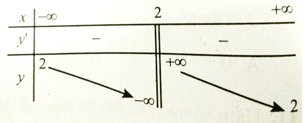
Bài 4: Hàm số nào sau đây có bảng biến thiên như hình bên?

Lời giải:

* Đồ thị hàm số đã cho có TCĐ là x =2, TCN là y = 2.

Hàm số nghịch biến trên TXĐ.

Bài 5: Hàm số y = x³ - 3x² + mx đạt cực tiểu tại x = 2 khi?

Lời giải:

Hàm số y = x³ - 3x² + mx đạt cực tiểu tại x = 2 khi và chỉ khi:

Bài 6: Hàm số

đồng biến trên tập xác định của nó khi:

Lời giải:

Hàm số 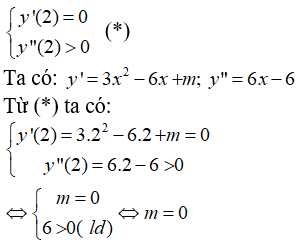 có tập xác định: D = R.

y'=x² + 2(m + 1)x - m - 1

Để hàm số đã cho đồng biến trên R khi và chỉ khi:

y' = f(x) = x² + 2(m + 1)x - m - 1 ≥ 0 ∀ x ∈ R

⇔ Δ' = (m + m + 1 = m² + 3m + 2 ≤ 0

⇔ -2 ≤ m ≤ -1

Bài 7: Cho đồ thị hàm số y = x³ - 2x² + 2x (C). Gọi x₁,x₂ là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2017 . Khi đó (x₁, x₂) bằng

Lời giải:

Tiếp tuyến của C vuông góc với đường thẳng y= -x + 2017 nên hệ số góc của tiếp tuyến là k₂ thỏa mãn (-1)k₂ = -1 => k₂ = 1

Suy ra k₂ = y' = 1 => 3x² - 4x + 2 <=> 3x² - 4x + 2 = 0 (*)

Vì x₁, x₂ là nghiệm của (*) nên áp dụng Vi-ét ta có x₁ + x₂ = $\frac{4}{3}$

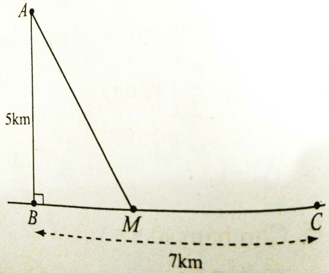
Bài 8: Một ngọn hải đăng đặt trại vị trí A cách bờbiển một khoảng AB = 5km. Trên bờ biển có một kho vị trí C cách B một khoảng là 7km. Do địa hình hiểm trở, người canh hải đăng chỉ có thể chèo thuyền từ A đến M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C, với vận tốc 6km/h. Vậy vị trí M cách B một khoảng bao xa thì người đó đến kho là nhanh nhất?

Lời giải:

Đặt BM = x (0 ≤ x ≤ 7) => MC = 7 - x. Áp dụng định lí Py-ta-go cho tam giác vuông ABM có

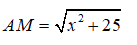
Thời gian đi từ A đến M là

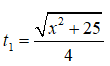
thời gian đi từ M đến C là

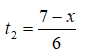
Tổng thời gian đi từ A đến C là

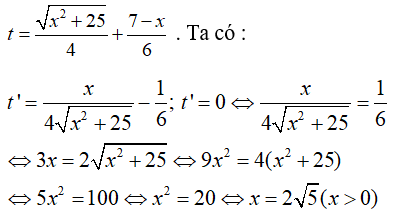
Bảng biến thiên

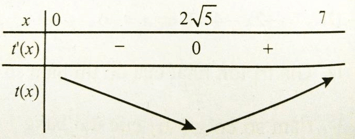
Để người đó đến kho nhanh nhất thì thời gian đi cần ít nhất, tức t đạt giá trị nhỏ nhất. Dựa vào bảng biến thiên ta thấy t đạt giá trị nhỏ nhất tại x = 2$\sqrt{5}$ ≈ 4,5

Vậy vị trí điểm M cách B một khoảng là 4,5km thì người đó đến kho là nhanh nhất.

Bài 9: Cho hàm số y = -x² - 4x + 3 có đồ thị (C). Nếu tiếp tuyến tại M của (C) có hệ số góc bằng 8 thì hoành độ điểm M là:

Lời giải:

Đạo hàm y’ = -2x - 4 = 8

Hệ số góc tại điểm có hoành độ x0 là: k = y'(x₀) = -2x₀ - 4

Để k = 8 thì -2x₀ - 4 = 8 ⇔ x₀ = -6

Vậy nếu tiếp tuyến tại M của (C) có hệ số góc bằng 8 thì hoành độ điểm M là -6.

Bài 10: Cho hàm số y = -x⁴ + 2x² - 1. Số giao điểm của đồ thị hàm số với trục Ox là:

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:

Số giao điểm của đồ thị hàm số với trục Ox là hai điểm.\

Câu 11: Diện tích hình phẳng giới hạn bởi y = (e + 1)x và y = (1 + e^x)x là:

Lời giải:

Phương trình hoành độ giao điểm:

Câu 12: Diện tích hình phẳng giới hạn bởi y = (x - 6)² và y = 6x - x² là:

Lời giải:

Phương trình hoành độ giao điểm:

Câu 13: Diện tích hình phẳng giới hạn bởi đường cong: y = x² + 1 , tiếp tuyến với đường cong này tại M(2;5) và trục Oy là:

Lời giải:

Ta có: y' = 4

Phương trình tiếp tuyến với y = x² + 1 tại M(2;5) là: y = 4(x - 2) + 5 = 4x - 3.

Ta có x² + 1 = 4x - 3 => x = 2 khi đó diện tích hình phẳng cần tính là:

Câu 14: Thể tích vật thể tròn xoay sinh ra bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi trục Ox và y = $\sqrt{x\sin x}$ với (0 ≤ x ≤ π) là:

Lời giải:

Câu 15: Tính thể tích vật thể tròn xoay quanh trục Ox sinh bởi hình phẳng giới hạn bởi các đường

 

Lời giải:

Thể tích vật thể tròn xoay là :

Câu 16: Tính thể tích vật thể tròn xoay quanh trục Oy sinh bởi hình phẳng giới hạn bởi các đường y = 2, y = 4 , y = $\frac{x^2}{2}$ .

Lời giải:

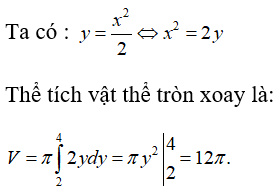
Câu 17: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = tanx, y = 0, x = 0, x = $\frac{\mathrm{\pi }}{3}$quanh Ox là:

Lời giải:

Thể tích vật thể tròn xoay là:

Câu 18: Diện tích hình phẳng giới hạn bởi ay = x² và ax = y² là:

Lời giải:

Câu 9: Một vật chuyển động với vận tốc

Quãng đường vật đi được sau 4s xấp xỉ bằng:

Lời giải:

Quãng đường vật di chuyển sau thời gian 4 giây bằng :

Xem thêm các dạng bài tập hay, có đáp án:

60 Bài tập về sự đồng biến, nghịch biến của hàm số (có đáp án năm 2024)

60 Bài tập về Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có đáp án năm 2024)

60 Bài tập về Khảo sát sự biến thiên và vẽ đồ thị hàm số (có đáp án năm 2024)

60 Bài tập về Hàm số lũy thừa (có đáp án năm 2024)

60 Bài tập về Hàm số mũ, Hàm số logarit (2024) có đáp án