60 Bài tập về Bất phương trình bậc nhất một ẩn (có đáp án năm 2024) - Toán 8

Bài giảng Toán 8 Bài 4: Bất phương trình bậc nhất một ẩn

Kiến thức cần nhớ

1. Định nghĩa bất phương trình bậc nhất một ẩn

Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b < 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a và b là hai số đã cho, a ≠ 0, được gọi là bất phương trình bậc nhất một ẩn.

Ví dụ 1.

2x – 3 > 0 là bất phương trình bậc nhất với ẩn x;

5(y + 2) – 1 ≤ 0 là bất phương trình bậc nhất với ẩn y.

2. Hai quy tắc biến đổi

a) Quy tắc chuyển vế

Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.

Ví dụ 2. Giải bất phương trình: x − 12 > 6.

Lời giải:

x − 12 > 6

$\iff$x > 6 + 12 (chuyển vế − 3 và đổi dấu thành 3)

$\iff$x > 18.

Vậy tập nghiệm của bất phương trình là {x | x > 18}.

b) Quy tắc nhân với một số

Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:

- Giữ nguyên chiều bất phương trình nếu số đó dương.

- Đổi chiều bất phương trình nếu số đó âm.

Ví dụ 3. Giải các bất phương trình:

a) 0,25x > 2;

b) $-\frac{1}{2}\mathrm{x}<5$.

Lời giải:

a) 0,25x ≥ 2

$\iff$0,25x . 4 ≥ 2 . 4 (nhân cả hai vế với 4)

$\iff$x ≥ 8.

Vậy tập nghiệm của bất phương trình là {x | x ≥ 8}.

b) $-\frac{1}{2}\mathrm{x}<5$

$\iff -\frac{1}{2}\mathrm{x}.\left(-2\right)>5.\left(-2\right)$(nhân cả hai vế với − 3 và đổi chiều)

$\iff$x > −10.

Vậy tập nghiệm của bất phương trình là {x | x > −10}.

3. Giải bất phương trình bậc nhất một ẩn

Áp dụng hai quy tắc biến đổi trên, ta giải bất phương trình bậc nhất một ẩn như sau:

Dạng ax + b > 0$\iff$ax > − b

$\iff$x > $-\frac{\mathrm{b}}{\mathrm{a}}$ nếu a > 0 hoặc x < $-\frac{\mathrm{b}}{\mathrm{a}}$ nếu a < 0.

Vậy bất phương trình có tập nghiệm là:

$\mathrm{S}=\left\{\begin{array}{l}\mathrm{a}>0\\ \mathrm{x}>-\frac{\mathrm{b}}{\mathrm{a}}\end{array}\right.$

Hoặc $\mathrm{S}=\left\{\begin{array}{l}\mathrm{a}<0\\ \mathrm{x}<-\frac{\mathrm{b}}{\mathrm{a}}\end{array}\right.$

Các dạng toán như ax + b < 0, ax + b ≤ 0, ax + b ≥ 0 tương tự như trên.

Ví dụ 4. Giải các phương trình: 4x – 6 > 0.

Lời giải:

4x – 6 > 0

$\iff$4x > 6 (chuyển –6 sang VP và đổi dấu)

$\iff$4x : 4 > 6 : 4 (chia cả hai vế cho 4)

$\iff \mathrm{x}>\frac{3}{2}$

Vậy tập nghiệm của bất phương trình là $\left\{\mathrm{x}|\mathrm{x}>\frac{3}{2}\right\}$.

4. Giải bất phương trình đưa được về dạng ax + b < 0; ax + b > 0; ax + b ≤ 0;  ax + b ≥ 0

Cách giải phương trình đưa được về dạng ax + b > 0: Để giải các phương trình đưa được về ax + b > 0, ta thường biến đổi phương trình như sau:

Bước 1: Quy đồng mẫu hai vế và khử mẫu (nếu có).

Bước 2: Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax > – b.

Bước 3: Tìm x.

Các phương trình đưa được về dạng ax + b < 0, ax + b ≤ 0 hoặc ax + b ≥ 0 làm tương tự như trên.

Ví dụ 5. Giải các phương trình: 4x – 6 > 2x + 5.

Lời giải:

4x – 6 > 2x + 5

$\iff$4x – 2x > 6 + 5

$\iff$2x > 11

$\iff$2x : 2 > 11 : 2

$\iff \mathrm{x}>\frac{11}{2}$

Vậy tập nghiệm của bất phương trình là $\left\{\mathrm{x}|\mathrm{x}>\frac{11}{2}\right\}$.

Bài tập có hướng dẫn

1. Bài tập vận dụng

Bài 1. Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) 3x – 12 < 0;

b) –2x + 16 < 0.

Lời giải:

a) 3x – 12 < 0

$\iff$3x < 12

$\iff$3x : 3 < 12 : 3

$\iff$x < 4.

Vậy tập nghiệm của bất phương trình là {x | x < 4}.

Biểu diễn tập nghiệm trên trục số:

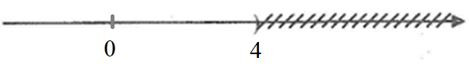
b) –2x + 16 < 0

$\iff$–2x < – 16

$\iff$–2x : (–2) > – 16 : (–2)

⇔ x > 8.

Vậy tập nghiệm của bất phương trình là {x | x > 8}.

Biểu diễn tập nghiệm trên trục số:

Bài 2. Giải các bất phương trình sau:

a) 6x – 16 < 2;

b) 4x – 1 ≥ 2x + 5.

Lời giải:

a) 6x – 16 < 2

$\iff$6x < 2 + 16

$\iff$6x < 18

$\iff$6x : 6 < 18 : 6

$\iff$x < 3.

Vậy tập nghiệm của bất phương trình là {x | x < 3}.

b) 4x – 1 ≥ 2x + 5

$\iff$4x – 2x ≥ 5 + 1

$\iff$2x ≥ 6

$\iff$2x : 3 ≥ 6 : 3

$\iff$x ≥ 2

Vậy tập nghiệm của bất phương trình là {x | x ≥ 2}.

Bài 3. Giải các bất phương trình sau:

a) $\frac{3\mathrm{x}-1}{4}>1$;

b) 5x + 4 ≥ 9x – 12.

Lời giải:

a) $\frac{3\mathrm{x}-1}{4}>1$

$\iff$3x – 1 > 4

$\iff$3x > 4 + 1

$\iff$3x > 5

$\iff$3x : 3 > 5 : 3

$\iff \mathrm{x}>\frac{5}{3}$

Vậy tập nghiệm của bất phương trình là $\left\{\mathrm{x}|\mathrm{x}>\frac{5}{3}\right\}$.

b) 5x + 4 ≥ 9x – 12

$\iff$5x – 9x ≥ – 12 – 4

$\iff$– 4x ≥ – 16

$\iff$– 4x : (– 4) ≤ – 16 : (– 4)

$\iff$x ≤ 4.

Vậy tập nghiệm của bất phương trình là {x | x ≤ 4}.

2. Bài tập tự luyện có hướng dẫn

(Xem trong file đính kèm)

Xem thêm các dạng bài tập liên quan khác:

200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)

100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)

500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2023)

60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024) có đáp án

300 Bài tập Toán 8 chương 4: Bất phương trình bậc nhất một ẩn (có đáp án năm 2023)