65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8

Bài giảng Toán 8 Bài 10: Chia đơn thức cho đơn thức

Lý thuyết

Khái niệm: Cho A và B là hai đơn thức, B ≠ 0.

Ta nói đơn thức A chia hết cho đơn thức B nếu tìm được một đơn thức Q sao cho

A = B.Q

A được gọi là đơn thức bị chia, B được gọi là đơn thức chia, Q được gọi là đơn thức thương.

Kí hiệu: Q = A : B hoặc $Q = \frac{A}{B}$ .

Nhận xét: Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.

Quy tắc: Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:

- Chia hệ số của đơn thức A cho hệ số của đơn thức B.

- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.

- Nhân các kết quả vừa tìm được với nhau.

Chú ý: Với mọi x ≠ 0, m, n ∈ ℕ, m ≥ n thì

x^m : xⁿ = x^{m – n} nếu m > n

x^m : xⁿ = 1 nếu m = n.

Ví dụ:

a) 15x²y⁵z : 5xy³z = (15 : 5)(x²: x)(y⁵: y³)(z : z) = 3xy².

b) 35x⁵y²: (−7x⁴y) =[35 : (−7)](x⁵: x⁴)(y²: y) = −5xy.

Các dạng bài tập chia đơn thức cho đơn thức

Dạng 1: Áp dụng quy tắc chia đơn thức cho đơn thức để thực hiện phép tính.

1. Phương pháp giải

Áp dụng quy tắc chia đơn thức cho đơn thức để tính.

2. Bài tập minh họa

Ví dụ 1: Thực hiện phép tính

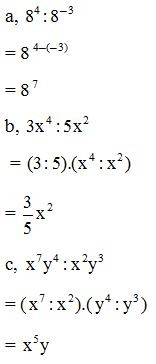
Cách chia đơn thức cho đơn thức, chia đa thức cho đơn thức chi tiết – Toán lớp 8 (ảnh 1)

Ví dụ 2: Tính

a) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 1

b) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 2

c) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 3

d) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 4

e) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 5

f) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 6

g) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 7

Hướng dẫn giải

a) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 8

b) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 9

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 10

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 11

e) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 12

f) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 13

g) 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 14

Ví dụ 3: Cho 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 15 . Tính giá trị của biểu thức với .

Hướng dẫn giải

Ta thu gọn P trước rồi thay giá trị của x và y vào biểu thức thu gọn để tính giá trị của biểu thức P.

Ta có:

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 18

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 19

Vậy 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 20 .

Ví dụ 4: Tính giá trị của biểu thức 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 21 với .

Hướng dẫn giải

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 23

Với 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 24 thì .

Dạng 2: Tìm điều kiện để biểu thức A chia hết cho biểu thức B

1. Phương pháp giải

Sử dụng lý thuyết về điều kiện về số mũ của các biến để đơn thức A chia hết cho đơn thức B.

2. Bài tập minh họa

Ví dụ 1: Tìm điều kiện của n để biểu thức A chia hết cho biểu thức B trong các trường hợp sau:

Cách chia đơn thức cho đơn thức, chia đa thức cho đơn thức chi tiết – Toán lớp 8 (ảnh 1)

Ví dụ 2: Tìm số tự nhiên n để phép chia sau là phép chia hết 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 27

Hướng dẫn giải

Để 65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8 - Ảnh 27 thì ta phải có .

Bài tập phân tích đa thức thành nhân tử

I. Bài tập trắc nghiệm chia đơn thức cho đơn thức

Câu 1: Kết quả của phép chia $24{x^3}{y^2}:12{x^2}y$ là:

A. $2xy$

B. $2{x^2}y$

C. $2x{y^2}$

D. $2{x^2}{y^2}$

Câu 2: Thương của phép chia $4x{y^2}:\frac{1}{2}xy$ là:

A. $8y$

B. $4y$

C. $8{x^2}{y^3}$

D. $4{x^2}{y^3}$

Câu 3: Kết quả của phép chia $\frac{{ - 5}}{6}x{y^2}:\frac{1}{2}y$ là:

A. $\frac{{ - 5}}{3}xy$

B. $\frac{5}{3}xy$

C. $\frac{{ - 3}}{5}xy$

D. $\frac{3}{5}xy$

Câu 4: Giá trị của biểu thức $15{x^{487}}{y^{937}}{z^{426}}:3{x^{486}}{y^{936}}{z^{425}}$ tại $x = 2;y = \frac{1}{5};z = \frac{1}{2}$ là:

A. 0

B. 8028

C. 1

D. 5829

Câu 5: Giá trị của biểu thức $\frac{1}{2}{y^3}{z^4}:5y{z^2}$ tại $y = 1;z = 10$ là:

A. 1

B. 10

C. 100

D. 1000

II. Bài tập tự luận chia đơn thức cho đơn thức

Bài 1: Thực hiện phép tính:

a, ${10^7}:{\left( { - 10} \right)^4}$

b, ${\left( {\frac{1}{4}} \right)^5}:{\left( {\frac{2}{8}} \right)^3}$

c, ${2^{16}}:{\left( { - 8} \right)^3}$

Bài 2: Thực hiện phép tính:

a, $\frac{1}{2}{x^2}{y^3}:\frac{3}{4}x{y^2}$

b, $\frac{5}{6}{x^7}{y^8}:\frac{1}{2}{x^6}{y^2}$

c, $12{x^3}{y^4}{z^2}:\left( {\frac{{ - 3}}{4}{x^2}{y^2}z} \right)$

d, $18{x^2}y:9y$

Bài 3: Tính giá trị của biểu thức:

a, $\frac{{15}}{7}{x^2}{y^2}{z^2}:\frac{1}{{14}}{x^2}yz$ tại $x = 29387;y = 1;z = - 1$

b, ${\left( { - xy} \right)^{15}}:{\left( { - xy} \right)^7}$ tại $x = 2;y = \frac{1}{2}$

c, $25{x^2}{y^4}:100{x^2}y$ tại $x = {49^{17}};y = 5$

C. Lời giải, đáp án bài tập chia đơn thức cho đơn thức

I. Bài tập trắc nghiệm chia đơn thức cho đơn thức

Câu 1	Câu 2	Câu 3	Câu 4	Câu 5
A	A	A	C	B

II. Bài tập tự luận chia đơn thức cho đơn thức

Bài 1:

a, ${10^7}:{\left( { - 10} \right)^4} = {10^7}:{10^4} = {10^3} = 1000$

b, ${\left( {\frac{1}{4}} \right)^5}:{\left( {\frac{2}{8}} \right)^3} = {\left( {\frac{1}{4}} \right)^5}:{\left( {\frac{1}{4}} \right)^3} = {\left( {\frac{1}{4}} \right)^2} = \frac{1}{{16}}$

c, ${2^{16}}:{\left( { - 8} \right)^3} = {2^{16}}:{\left( { - {2^3}} \right)^3} = {\left( { - 2} \right)^{16}}:{\left( { - 2} \right)^9} = {\left( { - 2} \right)^5} = - 32$

Bài 2:

a, $\frac{1}{2}{x^2}{y^3}:\frac{3}{4}x{y^2} = \left( {\frac{1}{2}:\frac{3}{4}} \right).\left( {{x^2}:x} \right).\left( {{y^3}:{y^2}} \right) = \frac{2}{3}xy$

b, $\frac{5}{6}{x^7}{y^8}:\frac{1}{2}{x^6}{y^2} = \left( {\frac{5}{6}:\frac{1}{2}} \right).\left( {{x^7}:{x^6}} \right).\left( {{y^8}:{y^2}} \right) = \frac{5}{3}x{y^6}$

c, $12{x^3}{y^4}{z^2}:\left( {\frac{{ - 3}}{4}{x^2}{y^2}z} \right) = \left( {12:\frac{{ - 3}}{4}} \right).\left( {{x^3}:{x^2}} \right).\left( {{y^4}:{y^2}} \right).\left( {{z^2}:z} \right) = - 16x{y^2}z$

d, $18{x^2}y:9y = \left( {18:9} \right).{x^2}.\left( {y:y} \right) = 2{x^2}$

Bài 3:

a, $\frac{{15}}{7}{x^2}{y^2}{z^2}:\frac{1}{{14}}{x^2}yz = 30{x^0}yz = 30.{\left( {29387} \right)^0}{.1^2}.{\left( { - 1} \right)^2} = 30$

b, ${\left( { - xy} \right)^{15}}:{\left( { - xy} \right)^7} = {\left( { - xy} \right)^8} = {\left( { - 2.\frac{1}{2}} \right)^8} = {\left( { - 1} \right)^8} = 1$

c, $25{x^2}{y^4}:100{x^2}y = \frac{1}{4}{x^0}{y^3} = \frac{1}{4}.{\left( {{{49}^{17}}} \right)^0}{.5^3} = \frac{{125}}{4}$

Được cập nhật 06/03/2024 262 lượt xem

Bởi Quynh Anh

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Toán 8

65 bài tập nhân đa thức với đa thức (có đáp án năm 2024) - Toán 8

1900.edu.vn xin giới thiệu: Tổng hợp các dạng bài tập nhân đa thức với đa thức Toán 8. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 8, giải bài tập Toán 8 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

378 6 tháng trước

Toán 8

85 Bài tập về chia đa thức cho đơn thức (có đáp án 2024) - Toán 8

1900.edu.vn xin giới thiệu: Tổng hợp các dạng bài tập chia đa thức cho đơn thức Toán 8. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 8, giải bài tập Toán 8 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

583 6 tháng trước

Toán 8

50 bài tập Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp có đáp án năm 2024 Toán 8

1k 6 tháng trước

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8

65 bài tập Chia đơn thức cho đơn thức có đáp án năm 2023 Toán 8

Lý thuyết

Các dạng bài tập chia đơn thức cho đơn thức

Dạng 1: Áp dụng quy tắc chia đơn thức cho đơn thức để thực hiện phép tính.

Dạng 2: Tìm điều kiện để biểu thức A chia hết cho biểu thức B

Bài tập phân tích đa thức thành nhân tử

Bình luận (0)

Bài viết cùng chủ đề

65 bài tập nhân đa thức với đa thức (có đáp án năm 2024) - Toán 8

85 Bài tập về chia đa thức cho đơn thức (có đáp án 2024) - Toán 8

50 bài tập Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp có đáp án năm 2024 Toán 8

Nội dung bài viết