Bài giảng Toán 8 Ôn tập chương 4
Kiến thức cần nhớ
1. Bất đẳng thức
Hệ thức dạng a < b (hay dạng a > b; a ≥ b; a ≤ b) được gọi là bất đẳng thức và gọi a là vế trái, b gọi là vế phải của bất đẳng thức.
2. Liên hệ giữa thứ tự và phép cộng
Tính chất: Cho ba số a, b và c, ta có:
Nếu a < b thì a + c < b + c;
Nếu a ≤ b thì a + c ≤ b + c;
Nếu a > b thì a + c > b + c;
Nếu a ≥ b thì a + c ≥ b + c.
3. Liên hệ giữa thứ tự và phép nhân với số dương
a) Tính chất
Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
b) Tổng quát
Với ba số a, b và c mà c > 0, ta có:
Nếu a < b thì ac < bc;
Nếu a ≤ b thì ac ≤ bc;
Nếu a > b thì ac > bc;
Nếu a ≥ b thì ac ≥ bc.
4. Liên hệ giữa thứ tự và phép nhân với số âm
a) Tính chất
Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được một bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.
b) Tổng quát
Với ba số a, b và c mà c < 0, ta có:
Nếu a < b thì ac > bc;
Nếu a ≤ b thì ac ≥ bc;
Nếu a > b thì ac < bc;
Nếu a ≥ b thì ac ≤ bc.
5. Bất phương trình một ẩn
- Định nghĩa bất phương trình một ẩn: Bất phương trình ẩn x là hệ thức A (x) > B (x) hoặc A (x) < B (x) hoặc A (x) ≥ B (x) hoặc A (x) ≤ B (x).
Trong đó: A (x) gọi là vế trái; B (x) gọi là vế phải.
- Nghiệm của bất phương trình là giá trị của ẩn để khi thay vào bất phương trình ta được một khẳng định đúng.
6. Định nghĩa bất phương trình bậc nhất một ẩn
Bất phương trình dạng ax + b < 0 (hoặc ax + b > 0, ax + b < 0, ax + b ≤ 0, ax + b ≥ 0) trong đó a và b là hai số đã cho, a ≠ 0, được gọi là bất phương trình bậc nhất một ẩn.
7. Hai quy tắc biến đổi
a) Quy tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
b) Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
- Giữ nguyên chiều bất phương trình nếu số đó dương.
- Đổi chiều bất phương trình nếu số đó âm.
8. Giải bất phương trình bậc nhất một ẩn
Áp dụng hai quy tắc biến đổi trên, ta giải bất phương trình bậc nhất một ẩn như sau:
Dạng ax + b > 0ax > − b.
x > nếu a > 0 hoặc x < nếu a < 0.
Vậy bất phương trình có tập nghiệm là:
Hoặc
Các dạng toán như ax + b < 0, ax + b ≤ 0, ax + b ≥ 0 tương tự như trên.
9. Giải bất phương trình đưa được về dạng ax + b < 0 ; ax + b > 0 ; ax + b ≤ 0; ax + b ≥ 0
Cách giải phương trình đưa được về dạng ax + b > 0: Để giải các phương trình đưa được về ax + b > 0, ta thường biến đổi phương trình như sau:
Bước 1: Quy đồng mẫu hai vế và khử mẫu (nếu có).
Bước 2: Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng ax > c.
Bước 3: Tìm x.
Các phương trình đưa được về dạng ax + b < 0, ax + b ≤ 0 hoặc ax + b ≥ 0 làm tương tự như trên.
10. Giá trị tuyệt đối
Giá trị tuyệt đối của số a, được kí hiệu là |a|, ta định nghĩa như sau:
11. Giải một số phương trình chứa dấu giá trị tuyệt đối
a) Phương pháp chung
Bước 1: Áp dụng định nghĩa giá trị tuyệt đối để loại bỏ dấu giá trị tuyệt đối.
Bước 2: Rút gọn hai vế của phương trình, giải phương trình.
Bước 3: Chọn nghiệm thích hợp trong từng trường hợp đang xét.
Bước 4: Kết luận nghiệm.
b) Một số dạng cơ bản
Dạng |A| = B
Cách 1: hoặc
Cách 2: hoặc
Dạng |A| = |B|A = B hoặc A = − B.
Dạng phương trình có chứa nhiều dấu giá trị tuyệt đối:
- Xét dấu các biểu thức chứa ẩn nằm trong dấu giá trị tuyệt đối.
- Chia trục số thành nhiều khoảng sao cho trong mỗi khoảng, các biểu thức nói trên có dấu xác định.
- Xét từng khoảng, khử các dấu giá trị tuyệt đối, rồi giải phương trình tương ứng trong trường hợp đó.
- Kết hợp các trường hợp đã xét, suy ra số nghiệm của phương trình đã cho.
Bài tập
1. Bài tập vận dụng (có đáp án)
Bài 1. Cho a > b, hãy so sánh:
a) a + 25 và b + 25;
b) a – 12 và b – 12.
Lời giải:
Bất đẳng thức: a > b.
a) Cộng cả hai vế của bất đẳng thức a > b với 25, ta được:
a + 25 > b + 25.
b) Cộng cả hai vế của bất đẳng thức a > b với (–12), ta được:
a + (–12) > b + (–12)
Hay a – 12 > b – 12.
Bài 2. Mỗi khẳng định sau đúng hay sai? Vì sao?
a) −5 > 3 + (−10);
b) 2 . (−6) < 2 . (−8);
c) −6 ≤ 2 . (−4);
d) x2 + 2 ≥ 2.
Lời giải:
(Kí hiệu: VP = vế phải; VT = vế trái).
a) Ta có: 3 + (−10) = − 7.
Vì − 5 > − 7 nên −5 > 3 + (−10).
Do đó khẳng định −5 > 3 + (−10) là đúng.
b) Ta có: 2 . (−6) = −12; 2 . (−8) = − 16.
Vì − 12 > − 16 nên 2 . (−6) > 2 . (−8).
Do đó khẳng định 2 . (−6) < 2 . (−8) là sai.
c) Ta có: 2 . (−4) = −8.
Vì −6 > −8 nên −6 > 2 . (−4)
Do đó khẳng định −6 ≤ 2 . (−4) là sai.
d) Với mọi số thực x ta có: x2 ≥ 0.
Suy ra x2 + 2 ≥ 2.
Do đó khẳng định x2 + 2 ≥ 2 đúng với mọi số thực x.
Vậy khẳng định a) và d) là đúng, khẳng định b) và c) là sai.
Bài 3. So sánh a và b nếu:
a) a – 34 ≤ b – 34;
b) 21 + a ≥ 21 + b
Lời giải:
a) Ta có: a – 34 ≤ b – 34
Cộng hai vế của bất đẳng thức
a – 34 ≤ b – 34 với 34, ta được:
a – 34 + 34 ≥ b – 34 + 34.
Do đó a ≥ b.
b) Ta có: 21 + a ≥ 21 + b.
Cộng hai vế của bất đẳng thức
21 + a ≥ 21 + b với (−21), ta được:
21 + a + (−21) ≥ 21 + b + (−21).
Do đó a ≥ b.
Bài 4. Số a là số âm, số 0 hay số dương nếu:
a) 10a > 2a;
b) −6b > 9b;
c) 8a ≤ 15a.
Lời giải:
a) Vì 10 > 2 mà 10a > 2a nên a là số dương;
b) Vì −6 < 9 mà −6a > 9a nên a là số âm;
c) Vì 8 < 15 mà 8a ≤ 15a nên a là số không âm (tức là a ≥ 0).
Bài 5. Đặt dấu thích hợp (<, >, =) vào chỗ chấm:
a) 5,12 . 2,4 ..... 5,12 . 3,1;
b) (–22) . 12,55 ..... (–22) . 45.
Lời giải:
a) Ta có 2,4 < 3,1 và 2,4 > 0.
Nhân hai vế của bất đẳng thức 2,4 < 3,1 với 2,4 ta được:
5,12 . 2,4 < 5,12 . 3,1.
b) Ta có 12,55 < 45 và –22 < 0.
Nhân hai vế của bất đẳng thức 12,55 < 45 với (–22), ta được:
(–22) . 12,55 > (–22) . 45.
Bài 6. Cho m > n, chứng minh:
a) m – 4 > n – 5;
b) 2m + 8 > 2n.
Lời giải:
a) Cộng hai vế của bất đẳng thức m > n với – 4, ta được:
m – 4 > n – 4. (1)
Cộng hai vế của bất đẳng thức – 4 > – 5 với n, ta được:
n – 4 > n – 5. (2)
Từ (1) và (2), theo tính chất bắc cầu, suy ra:
m – 4 > n – 5.
b) Nhân hai vế của bất đẳng thức m > n với 2, ta được:
2m > 2n.
Cộng hai vế của bất đẳng thức 2m > 2n với 8, ta được:
2m + 8 > 2n + 8. (3)
Cộng hai vế của bất đẳng thức 8 > 0 với 2n, ta được:
2n + 8 > 2n. (4)
Từ (3) và (4), theo tính chất bắc cầu, suy ra:
2m + 8 > 2n.
Bài 7. Kiểm tra xem giá trị x = 2 là nghiệm của bất phương trình nào trong các bất phương trình sau:
a) 2x – 5 < 10
b) −4x > 3x + 7
c) 5 – 2x > 4x – 6
Lời giải:
Thay x = 2 lần lượt vào từng vế của mỗi bất phương trình, ta được:
a) 2x – 5 = 2 . 2 – 5 = – 1 < 10.
Vậy x = 2 là nghiệm của bất phương trình 2x + 3 < 9.
b) – 4x = – 4 . 2 = – 8;
3x + 7 = 3 . 2 + 7 = 13
Vì – 8 < 13 nên x = 2 không phải nghiệm của bất phương trình −4x > 3x + 7.
c) 5 – 2x > 4x – 6
5 – 2x = 5 – 2 . 2 = 1;
4x – 6 = 4 . 2 – 6 = 2.
Vì 1 < 2 nên x = 2 không phải là nghiệm của bất phương trình 5 – x > 3x – 12.
Bài 8. Viết và biểu diễn tập nghiệm trên trục số bất phương trình x ≤ −6.
Lời giải:
Tập nghiệm của bất phương trình x ≤ −6 là tập hợp các số nhỏ hơn hoặc bằng −6, tức là tập hợp {x | x ≤ −6}.
Ta biểu diễn tập hợp này trên trục số như hình vẽ:

Bài 9. Hình vẽ sau đây biểu diễn tập nghiệm của bất phương trình nào? (Chỉ nêu một bất phương trình).
a)
![]()
b)
![]()
c)
![]()
Lời giải:
a) Hình a) biểu diễn tập nghiệm của bất phương trình x > 4;
b) Hình b) biểu diễn tập nghiệm của bất phương trình x < −5;
c) Hình c) biểu diễn tập nghiệm của bất phương trình x ≥ 2.
Bài 10. Giải các bất phương trình sau:
a) 6x – 16 < 2;
b) 4x – 1 ≥ 2x + 5.
Lời giải:
a) 6x – 16 < 2
6x < 2 + 16
6x < 18
6x : 6 < 18 : 6
x < 3.
Vậy tập nghiệm của bất phương trình là {x | x < 3}.
b) 4x – 1 ≥ 2x + 5
4x – 2x ≥ 5 + 1
2x ≥ 6
2x : 3 ≥ 6 : 3
x ≥ 2
Vậy tập nghiệm của bất phương trình là {x | x ≥ 2}.
Bài 11. Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a) 3x – 12 < 0;
b) –2x + 16 < 0
Lời giải:
a) 3x – 12 < 0
3x < 12
3x : 3 < 12 : 3
x < 4.
Vậy tập nghiệm của bất phương trình là {x | x < 4}.
Biểu diễn tập nghiệm trên trục số:
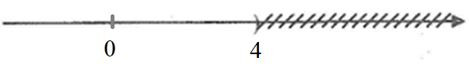
b) –2x + 16 < 0
–2x < – 16
–2x : (–2) > – 16 : (–2)
⇔ x > 8.
Vậy tập nghiệm của bất phương trình là {x | x > 8}.
Biểu diễn tập nghiệm trên trục số:
![]()
Bài 12. Giải các bất phương trình sau:
a) ;
b) 5x + 4 ≥ 9x – 12.
Lời giải:
a)
3x – 1 > 4
3x > 4 + 1
3x > 5
3x : 3 > 5 : 3
Vậy tập nghiệm của bất phương trình là .
b) 5x + 4 ≥ 9x – 12
5x – 9x ≥ – 12 – 4
– 4x ≥ – 16
– 4x : (– 4) ≤ – 16 : (– 4)
x ≤ 4.
Vậy tập nghiệm của bất phương trình là {x | x ≤ 4}.
Bài 13. Giải các phương trình sau:
a) |5x| = 4x – 8;
b) |2x| + 12 = 3x;
c) |x + 2| = 3x – 14.
Lời giải:
a) Ta có |5x| = 4x − 8.
+ Với x ≥ 0 ta có |5x| = 5x.
Khi đó, phương trình trở thành 5x = 4x – 8.
5x − 4x = −8
x = −8 (không thỏa mãn điều kiện x ≥ 0).
Do đó x = −8 không phải là một nghiệm của phương trình đã cho.
+ Với x < 0 ta có |5x| = −5x
Khi đó, phương trình trở thành −5x = 4x − 8
−2x − 4x = −8
−6x = −8
(không thỏa mãn điều kiện x < 0).
Do đó không phải là một nghiệm của phương trình đã cho.
Vậy phương trình đã cho có vô nghiệm.
b) Ta có |2x| + 12 = 3x.
+ Với x ≥ 0 ta có |2x| = 2x
Khi đó, phương trình trở thành 2x + 12 = 3x
2x − 3x = −12
−x = −12
x = 12 (thỏa mãn điều kiện x ≥ 0).
Do đó x = 12 là một nghiệm của phương trình đã cho.
+ Với x < 0 ta có |2x| = −2x
Khi đó, phương trình trở thành −2x + 12 = 3x
−2x − 3x = −12
−5x = −12
(không thỏa mãn điều kiện x < 0).
Do đó không phải là một nghiệm của phương trình đã cho.
Vậy phương trình đã cho có tập nghiệm là S = {12}.
c) Ta có |x + 2| = 3x – 14.
+ Với x + 2 ≥ 0 hay x ≥ –2 ta có |x + 2| = x + 2.
Khi đó, phương trình trở thành x + 2 = 3x – 14
x − 3x = −14 – 2
−2x = −16
x = 8 (thỏa mãn điều kiện x ≥ 0).
Do đó x = 8 là một nghiệm của phương trình đã cho.
+ Với x < 0 ta có |x + 2| = − (x + 2) = – x – 2.
Khi đó, phương trình trở thành – x – 2 = 3x – 14
−x − 3x = 2 −14
−4x = −12
x = 3 (không thỏa mãn điều kiện x < 0).
Do đó x = 3 không phải là một nghiệm của phương trình đã cho.
Vậy phương trình đã cho có tập nghiệm là S = {8}.
Bài 14. Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức sau:
a) A = 3x + 2 + |4x| với x > 0.
b) B = |x – 3| – 2x + 8 với x > 3.
c) C = |x – 5| – x + 2 với x < 5.
Lời giải:
a) Khi x > 0 ta có 4x > 0 nên |4x| = 4x.
Do đó A = 3x + 2 + |4x| = 3x + 2 + 4x = 7x + 2.
b) Khi x > 3 ta có x – 3 > 0 nên |x – 3| = x – 3.
Do đó B = |x – 3| – 2x + 8 = x – 3 – 2x + 8 = 5 – x.
c) Khi x < 5 ta có x – 5 < 0 nên |x – 5| = – (x – 5) = 5 – x.
Do đó C = |x – 5| – x + 2 = 5 – x – x + 2 = 7 – 2x.
2. Bài tập tự luyện theo các dạng có hướng dẫn
(Xem thêm trong file đính kèm)
Xem thêm các dạng bài tập liên quan khác:
200 Bài tập Bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)
100 Bài tập hệ bất phương trình bậc nhất hai ẩn (có đáp án năm 2023)
500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2023)
60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024) có đáp án
300 Bài tập Toán 8 chương 4: Bất phương trình bậc nhất một ẩn (có đáp án năm 2023)












