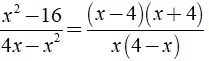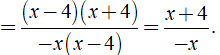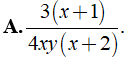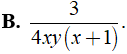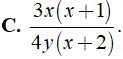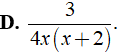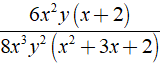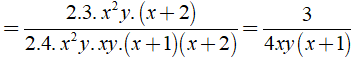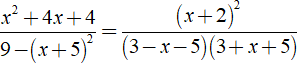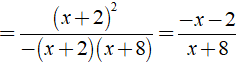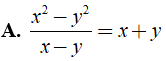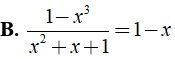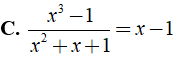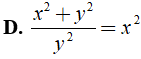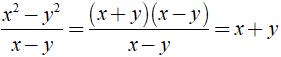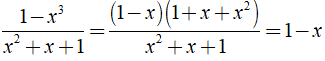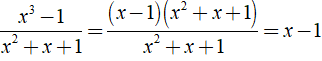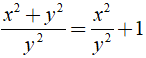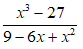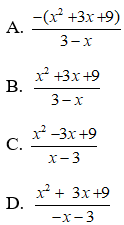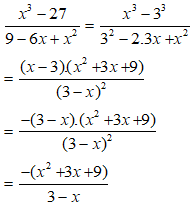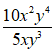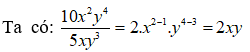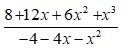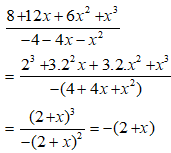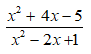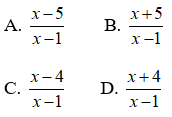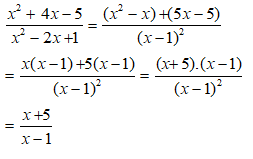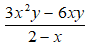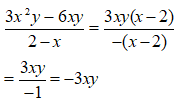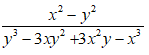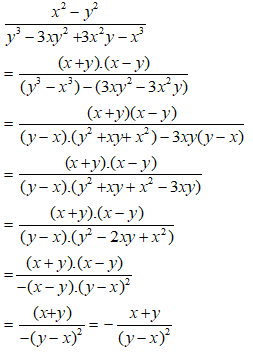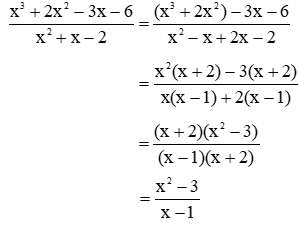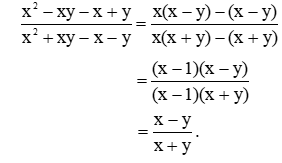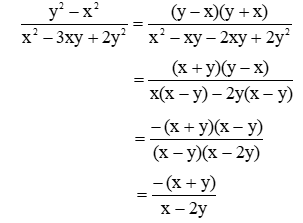50 bài tập về rút gọn phân thức đại số (có đáp án 2024) – Toán 8

Rút gọn phân thức đại số và cách giải bài tập - Toán lớp 8

I. Lý thuyết

Để rút gọn phân thức cho trước ta làm như sau

Bước 1: Sử dụng các phương pháp phân tích đa thức thành nhân tử để biến đổi cả tử thức và mẫu thức.

Bước 2: Sử dụng các tính chất cơ bản của phân thức đã học để rút gọn phân thức đã cho.

Nhắc lại các tính chất cơ bản của phân thức

- Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác 0 thì được phân thức mới bằng phân thức đã cho.

$\frac{A}{B}=\frac{A.M}{B.M}$(với $\frac{A}{B}$là phân thức; B, M  0)

- Nếu chia cả tử và mẫu của một phân thức cho một nhân tử chung của tử và mẫu ta được một phân thức mới bằng phân thức đã cho.

$\frac{A}{B}=\frac{A:N}{B:N}$(với N là nhân tử chung của A và B)

- Nếu đổi dấu cả tử và mẫu của một phân thức đã cho thì ta được phân thức mới bằng phân thức ban đầu.

$\frac{A}{B}=\frac{-A}{-B}$(với B$\ne$0)

- Nếu đổi dấu tử hoặc mẫu của phân thức và đồng thời đổi dấu phân thức ta được phân thức mới bằng phân thức đã cho.

$\frac{A}{B}=-\frac{-A}{B}=-\frac{A}{-B}$(với B$\ne$0)

II. Các dạng bài tập

Dạng 1: Rút gọn phân thức

Phương pháp giải: Ta thực hiện theo hai bước sau

Bước 1: Phân tích tử thức và mẫu thức thành nhân tử để tìm nhân tử chung.

Bước 2: Rút gọn bằng cách triệt tiêu nhân tử chung.

Chú ý: Có khi cần đổi dấu ở tử hoặc mẫu để nhận ra nhân tử chung của tử và mẫu (lưu ý tới tính chất A = – (– A)).

Ví dụ 1: Rút gọn phân thức sau: $\frac{2x^3-x^2-2x+1}{x^3+3x^2-x-3}$với $x\ne -3;x\ne \pm 1$

Lời giải:

$\frac{2x^3-x^2-2x+1}{x^3+3x^2-x-3}$

$=\frac{x^2\left(2x-1\right)-\left(2x-1\right)}{x^2\left(x+3\right)-\left(x+3\right)}$

$=\frac{\left(2x-1\right)\left(x^2-1\right)}{\left(x+3\right)\left(x^2-1\right)}$

$=\frac{2x-1}{x+3}$với $x\ne -3;x\ne \pm 1$

Ví dụ 2: Đơn giản phân thức sau$\frac{9x^2{y}^2+3x^2}{12x{y}^5+4x{y}^3}$với $x,y\ne 0$

Lời giải:

$\frac{9x^2{y}^2+3x^2}{12x{y}^5+4x{y}^3}$

$=\frac{3x^2\left(3y^2+1\right)}{4x{y}^3\left(3y^2+1\right)}$

$=\frac{3x^2}{4x{y}^3}$

$=\frac{3x}{4y^3}$ với $x,y\ne 0$

Dạng 2: Chứng minh đẳng thức

Phương pháp giải: Chọn 1 trong ba cách biến đổi sau

Cách 1: Biến đổi vế trái thành vế phải

Cách 2: Biến đổi vế phải thành vế trái

Cách 3: Biến đổi đồng thời cả hai vế

Chú ý: Sử dụng các tính chất cơ bản của phân thức để biến đổi, rút gọn.

Ví dụ 1: Chứng minh đẳng thức:

$\frac{2x^2+3xy+y^2}{2x^3+x^{2}y-2x{y}^2-y^3}=\frac{1}{x-y}$với $y\ne -2x;y\ne \pm x$

Lời giải:

Đặt $VT=\frac{2x^2+3xy+y^2}{2x^3+x^{2}y-2x{y}^2-y^3}$

$VP=\frac{1}{x-y}$

Ta biến đổi vế trái

$VT=\frac{2x^2+3xy+y^2}{2x^3+x^{2}y-2x{y}^2-y^3}$

$\iff VT=\frac{2x^2+2xy+xy+y^2}{2x^3+x^{2}y-2x{y}^2-y^3}$

$\iff VT=\frac{2x\left(x+y\right)+y\left(x+y\right)}{x^2\left(2x+y\right)-y^2\left(2x+y\right)}$

$\iff VT=\frac{\left(2x+y\right)\left(x+y\right)}{\left(x^2-y^2\right)\left(2x+y\right)}$

$\iff VT=\frac{x+y}{\left(x+y\right)\left(x-y\right)}$

$\iff VT=\frac{1}{x-y}=VP$(điều phải chứng minh)

Ví dụ 2: Cho $P=\frac{4x{y}^2-4x^{2}y+x^3}{4x^3-8x^{2}y}$và $Q=\frac{2xy-x^2-2y+x}{4x-4x^2}$

Với $x\ne 0;x\ne 1;x\ne 2y$

Chứng minh P = Q

Lời giải:

Ta có:

$P=\frac{4x{y}^2-4x^{2}y+x^3}{4x^3-8x^{2}y}$

$P=\frac{x\left(4y^2-4xy+x^2\right)}{4x^2\left(x-2y\right)}$

$P=\frac{x{\left(x-2y\right)}^2}{4x^2\left(x-2y\right)}$

$P=\frac{x-2y}{4x}$ (1)

Ta lại có

$Q=\frac{2xy-x^2-2y+x}{4x-4x^2}$

$Q=\frac{\left(2xy-2y\right)+\left(x-x^2\right)}{4x-4x^2}$

$Q=\frac{2y\left(x-1\right)-x\left(x-1\right)}{-4x\left(x-1\right)}$

$Q=\frac{\left(x-1\right)\left(2y-x\right)}{-4x\left(x-1\right)}$

$Q=\frac{2y-x}{-4x}$

$Q=\frac{x-2y}{4x}$(2)

Từ (1) và (2) $\Rightarrow P=Q$ (điểu phải chứng minh)

Dạng 3: Chứng minh một phân thức là phân thức tối giản

Phương pháp giải: Ta chứng minh tử thức và mẫu thức có ước chung lớn nhất là 1 hoặc -1

Bước 1: Gọi ước chung lớn nhất của tử thức và mẫu thức là d

Bước 2: Chứng minh d$=\pm$ 1

Chú ý: Cần vận dụng các kiến thức liên quan đến ước và bội, tính chất chia hết…

+ Khi a chia hết cho b, ta nói a là bội của b và b là ước của a.

+ Tính chất chia hết của một tổng(hiệu): $\left.\begin{array}{l}a⋮m\\ b⋮m\end{array}\right\}\Rightarrow \left(a\pm b\right)⋮m$

+ Tính chất chia hết của một tích: $a⋮m\Rightarrow \text{\hspace{0.17em}\hspace{0.17em}}ka⋮m.$

Ví dụ 1: Chứng minh các phân thức sau tối giản với mọi số tự nhiên n:

a) $\frac{3n+1}{5n+2}$

b) $\frac{2n-1}{4n^2-2}$

Lời giải:

a) $\frac{3n+1}{5n+2}$

Gọi ước chung lớn nhất của 3n + 1 và 5n + 2 là d

$\Rightarrow \left\{\begin{array}{l}\left(3n+1\right)⋮d\\ \left(5n+2\right)⋮d\end{array}\right.$

$\iff \left\{\begin{array}{l}5.\left(3n+1\right)⋮d\\ 3.\left(5n+2\right)⋮d\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(15n+5\right)⋮d\\ \left(15n+6\right)⋮d\end{array}\right.$

$\Rightarrow \left[\left(15n+6\right)-\left(15n+5\right)\right]⋮d$      (áp dụng tính chất chia hết của một hiệu)

$\iff \left(15n+6-15n-5\right)⋮d$

$\iff 1⋮d$

$\Rightarrow d=1$hoặc d = -1

Vậy $\frac{3n+1}{5n+2}$là phân số tối giản với $\forall n\in \mathbb{N}$

b) $\frac{2n-1}{4n^2-2}$

Gọi ước chung của 2n – 1 và $4n^2-2$ là d

$\Rightarrow \left\{\begin{array}{l}\left(2n-1\right)⋮d\\ \left(4n^2-2\right)⋮d\end{array}\right.$

$\iff \left\{\begin{array}{l}2n\left(2n-1\right)⋮d\\ \left(4n^2-2\right)⋮d\end{array}\right.$        (áp dụng tính chất chia hết của một tích)

$\iff \left\{\begin{array}{l}\left(4n^2-2n\right)⋮d\\ \left(4n^2-2\right)⋮d\end{array}\right.$

$\Rightarrow \left[\left(4n^2-2n\right)-\left(4n^2-2\right)\right]⋮d$     (áp dụng tính chất chia hết của một hiệu).

$\iff \left(4n^2-2n-4n^2+2\right)⋮d$

$\iff \left(-2n+2\right)⋮d$

$\Rightarrow \left[\left(-2n+2\right)+\left(2n-1\right)\right]⋮d$    (áp dụng tính chất chia hết của một tổng)

$\iff \left(-2n+2+2n-1\right)⋮d$

$\iff 1⋮d$$\Rightarrow d=1$ hoặc d = -1

Vậy phân thức đã cho tối giản với $\forall n\in \mathbb{N}$

Ví dụ 2: Trong các phân thức sau, phân thức nào tối giản

a) $\frac{2n^2+1}{n^2+1}$

b) $\frac{2n+1}{2n+3}$

Lời giải:

a) $\frac{2n^2+1}{n^2+1}$

Gọi d là ước chung lớn nhất của $2n^2+1$và $n^2+1$

$\Rightarrow \left\{\begin{array}{l}\left(2n^2+1\right)⋮d\\ \left(n^2+1\right)⋮d\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(2n^2+1\right)⋮d\\ 2\left(n^2+1\right)⋮d\end{array}\right.$

$\iff \left\{\begin{array}{l}\left(2n^2+1\right)⋮d\\ \left(2n^2+2\right)⋮d\end{array}\right.$

$\Rightarrow \left[\left(2n^2+1\right)-\left(2n^2+2\right)\right]⋮d$

$\iff \left(2n^2+1-2n^2-2\right)⋮d$

$\iff -1⋮d$

$\Rightarrow d=1$ hoặc d = -1

Vậy phân thức $\frac{2n^2+1}{n^2+1}$tối giản.

b) $\frac{2n+1}{2n+3}$

Gọi ước chung lớn nhất của 2n + 1 và 2n + 3 là d

$\Rightarrow \left\{\begin{array}{l}\left(2n+1\right)⋮d\\ \left(2n+3\right)⋮d\end{array}\right.$

$\Rightarrow \left[\left(2n+1\right)-\left(2n+3\right)\right]⋮d$

$\iff \left(2n+1-2n-3\right)⋮d$

$\iff -2⋮d$

=>  Ngoài hai ước là 1 và  – 1 thì tử thức và mẫu thức đã cho còn có thêm ít nhất một ước nữa là 2.

Vậy phân thức $\frac{2n+1}{2n+3}$không là phân thức tối giản.

Dạng 4: Tìm giá trị nguyên của biến x để phân thức đạt giá trị nguyên

Phương pháp giải: Phân thức $\frac{A\left(x\right)}{B\left(x\right)}$

Bước 1: Chia A(x) cho B(x). Khi đó ta được $\frac{A\left(x\right)}{B\left(x\right)}=C\left(x\right)+\frac{m}{B\left(x\right)}$

Với C(x) là đa thức nhận giá trị nguyên khi x nguyên, m là số nguyên

Bước 2: Để $\frac{A\left(x\right)}{B\left(x\right)}$ nguyên  thì $\frac{m}{B\left(x\right)}$ nguyên hay B(x) $\in$Ư(m)

Bước 3: Tìm các giá trị x thỏa mãn và kết luận.

Ví dụ: Tìm x nguyên để các phân thức sau nhận giá trị nguyên

a) $\frac{3}{x+1}$

b) $\frac{6x+4}{2x-1}$

Lời giải:

a) Để phân thức $\frac{3}{x+1}$ nguyên thì $\left(x+1\right)\in$Ư(3) với điều kiện x-1

Ư(3) = $\left\{-3;-1;1;3\right\}$

Vậy để phân thức $\frac{3}{x+1}$ nguyên thì $x\in \left\{-4;-2;0;2\right\}$

b) $\frac{6x+4}{2x-1}=\frac{6x-3+7}{2x-1}=\frac{3\left(2x-1\right)}{2x-1}+\frac{7}{2x-1}=3+\frac{7}{2x-1}$ với x $\ne \frac{1}{2}$

Để $\frac{6x+4}{2x-1}$ nguyên thì $3+\frac{7}{2x-1}$ nguyên hay $\frac{7}{2x-1}$

$\Rightarrow \left(2x-1\right)\in$Ư(7)

Ư(7) = $\left\{-7;-1;1;7\right\}$

Vậy để phân thức $\frac{6x+4}{2x-1}$ nguyên thì $x\in \left\{-3;0;1;4\right\}$

III. Bài tập vận dụng

I. Bài tập trắc nghiệm

Bài 1: Kết quả của rút gọn biểu thức $\frac{\left(6x^2{y}^2\right)}{\left(8x{y}^5\right)}$ là ?

A. $\frac{6}{8}$   

B. $\frac{3x}{\left(4y^3\right)}$

C. 2xy²   

D. $\frac{\left(x^2{y}^2\right)}{\left(x{y}^5\right)}$

Lời giải:

Điều kiện xác định là x ≠ 0;y ≠ 0.

Ta có $\frac{\left(6x^2{y}^2\right)}{\left(8x{y}^5\right)}$ = $\frac{(2.3.x{y}^2.x)}{(2.4.x{y}^2.y^3)}$ = $\frac{3x}{4y^3}$

Chọn đáp án B.

Bài 2: Kết quả của rút gọn biểu thức $\frac{\left(x^2-16\right)}{\left(4x-x^2\right)}$ ( x ≠ 0, x ≠ 4 ) là ?

A. $\frac{\left(x-4\right)}{x}$

B. $\frac{x+4}{x-4}$

C. $\frac{\left(x+4\right)}{\left(-x\right)}$

D. $\frac{\left(4-x\right)}{\left(-x\right)}$

Lời giải:

Điều kiện xác định là

Ta có 

Chọn đáp án C.

Bài 3: Rút gọn biểu thức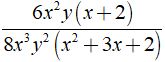 là

Lời giải:

Điều kiện xác định x,y ≠ 0; x² + 3x + 2 ≠ 0

Ta có: 

Chọn đáp án B.

Bài 4: Rút gọn phân thức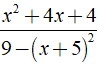 được kết quả là ?

A. $\frac{\left(-x-2\right)}{\left(x+8\right)}$

B. $\frac{\left(x+2\right)}{\left(x-8\right)}$

C. $\frac{\left(x+2\right)}{\left(x+8\right)}$

D. $\frac{\left(-x-2\right)}{\left(x-8\right)}$

Lời giải:

Điều kiện xác định: 9 - ( x + 5 )² ≠ 0.

Ta có: 

Chọn đáp án A.

Bài 5: Cho kết quả sai trong các phương án sau đây ?

Lời giải:

Ta có:

+

⇒ Đáp án A đúng.

+

⇒ Đáp án B đúng.

+

⇒ Đáp án C đúng.

+

⇒ Đáp án D sai.

Chọn đáp án D.

Bài 6: Rút gọn phân thức sau:

Lời giải:

Chọn đáp án A

Bài 7: Rút gọn biểu thức sau:

A. 2x    

B. 2xy²

C. 2xy    

D. 2x²y

Lời giải:

Chọn đáp án C

Bài 8: Rút gọn biểu thức sau:

A. – 2 + x    

B. 2 + x

C. – 2 – x    

D. 2 – x

Lời giải:

Chọn đáp án C

Bài 9: Rút gọn biểu thức sau:

Lời giải:

Chọn đáp án B

Bài 10: Rút gọn biểu thức sau:

A. 3xy    

B. – 3xy

C. 3x²    

D. 3y

Lời giải:

Chọn đáp án B

II. Bài tập tự luận

Bài 1: Rút gọn phân thức sau:

Lời giải:

Bài 2: Rút gọn phân thức 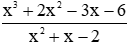 ta được phân thức có tử là?

Lời giải

Ta có:

Bài 3: Rút gọn phân thức 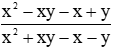 ta được phân thức có mẫu là?

Lời giải

Ta có:

Vậy mẫu thức của phân thức đã rút gọn là x + y.

Bài 4: Mẫu thức của phân thức 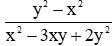 sau khi thu gọn có thể là?

Lời giải

Ta có:

Vậy mẫu thức của phân thức đã rút gọn là x - 2y.

Bài 5: Tìm x biết a²x - ax + x = a³ + 1?

Lời giải

Ta có: a²x - ax + x = a³ + 1

⇔ x(a² - a + 1) = (a + 1)(a2 - a + 1)

⇔ x = a + 1 vì a² - a + 1 = 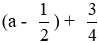 ≠ 0, ∀a.

Vậy x = a + 1.

Bài 6: Rút gọn các phân thức sau:

a) $\frac{12x^3{y}^2}{18x{y}^5}$

b) $\frac{15x(x+5{)}^3}{20x^2(x+5)}$

Lời giải: 

a) $\frac{12x^3{y}^2}{18x{y}^5}=\frac{2x^2.6x{y}^2}{3y^3.6x{y}^2}=\frac{2x^2}{3y^3}$

b) $\frac{15x(x+5{)}^3}{20x^2(x+5)}=\frac{3.(x+5{)}^2.5x(x+5)}{4x.5x.(x+5)}=\frac{3(x+5{)}^2}{4x}$

Bài 7:

a) $\frac{7x^2+14x+7}{3x^2+3x}$

b) $\frac{45x(3-x)}{15x(x-3{)}^3}$

Lời giải:

a) $\frac{7x^2+14x+7}{3x^2+3x}=\frac{7(x^2+2x+1)}{3x(x+1)}=\frac{7(x+1{)}^2}{3x(x+1)}=\frac{7(x+1)}{3x}$

b) $\frac{45x(3-x)}{15x(x-3{)}^3}=\frac{3.(3-x)}{(x-3{)}^3}=\frac{-3(x-3)}{(x-3{)}^3}=\frac{-3}{(x-3{)}^2}$

Tìm nhân tử chung của cả tử và mẫu.

Lời giải:

Ta có: $4x^3=2x^2.2x$ và $10x^2.y=2x^2.5y$

Nên nhân tử chung của cả tử và mẫu là $2x^2$

Bài 9: Cho phân thức: $\frac{4x^3}{10x^{2}y}$ Chia cả tử và mẫu cho nhân tử chung.

Lời giải:

${\displaystyle \frac{4x^3}{10x^{2}y}}={\displaystyle \frac{4x^3:2x^2}{10x^{2}y:2x^2}}={\displaystyle \frac{2x}{5y}}$

Bài 10: Cho phân thức: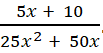 

a) Phân tích tử và mẫu thành nhân tử rồi tìm nhân tử chung của chúng.

b) Chia cả tử và mẫu cho nhân tử chung.

Lời giải:

a) 5x + 10 = 5(x + 2)

25x² + 50x = 25x(x + 2)

⇒ Nhân tử chung của chúng là: 5(x + 2)

b)

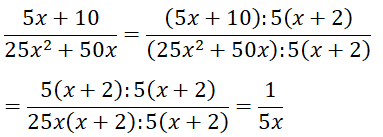
III. Bài tập tự luyện

Bài 1. Chứng minh các cặp phân thức sau bằng nhau:

a) $\frac{3}{2x-3}$ và $\frac{3x+6}{2x^2+x-6}$

b) $\frac{2}{x+4}$ và $\frac{2x^2+6x}{x^3+7x^2+12x}$

c) $\frac{x^2-5x+4}{x^3-1}=\frac{x-4}{x^2+x+1}$

d) $\frac{x^2-3x+2}{4-x^2}=\frac{1-x}{x+2}$

Bài 2. Rút gọn các phân thức sau:

a) $\frac{y(2x-x^2)}{x(2y+y^2)}$ 

b) $\frac{x{y}^3-y{x}^3}{x^2+xy}$

c) $\frac{(x+a{)}^2-x^2}{a^2+4x^2+4ax}$

d) $\frac{(x+a{)}^2-4x^2}{a^2+9x^2+6ax}$

e) $\frac{y(2x-x^2)(y+2)}{x(2y+y^2)(x-2)}$

f) $\frac{(x{y}^3-y{x}^3)(x-y)}{(x^2+xy)(x+y)}$

Bài 3: Rút gọn các phân thức sau:

a) $\frac{x^3-5x^2+6x}{-4x^2+10x-4}$

b) $\frac{x^2-3xy+2y^2}{x^3+2x^{2}y-x{y}^2-2y^3}$

Bài 4:

Áp dụng qui tắc đổi dấu rồi rút gọn phân thức:

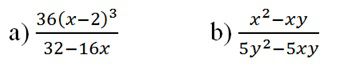
Bài 5: Rút gọn phân thức:

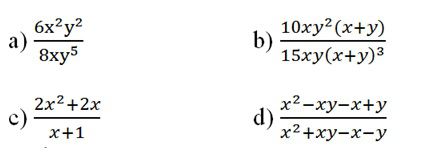
Bài 6: Rút gọn phân thức:

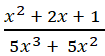
Bài 7: Rút gọn phân thức :

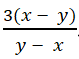
Bài 8: Rút gọn phân thức:

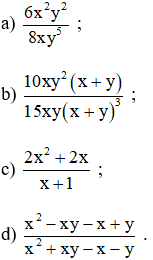
Bài 9: Trong tờ nháp của một bạn có ghi một số phép rút gọn phân thức như hình sau:

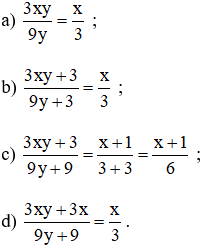
Theo em câu nào đúng, câu nào sai? Em hãy giải thích.

Bài 10: Áp dụng qui tắc đổi dấu rồi rút gọn phân thức:

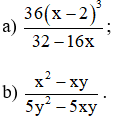
Xem thêm các dạng bài tập hay, có đáp án:

60 Bài tập về Rút gọn phân thức (có đáp án năm 2024) - Toán 8

50 Bài tập Rút gọn biểu thức chứa căn thức bậc hai (có đáp án năm 2024) - Toán 9

20 Bài tập Cách Rút gọn biểu thức chứa căn bậc hai (2024) cực hay, có đáp án (dạng √(A2))

50 bài tập về rút gọn biểu thức hữu tỉ (có đáp án 2024 ) – Toán 8

50 Bài tập Rút gọn phân số (có đáp án năm 2024) - Toán lớp 5