50 bài tập về hình thoi (có đáp án 2024) – Toán 8 chi tiết nhất

Các dạng toán về Hình thoi và cách giải - Toán lớp 8

I. Kiến thức cần nhớ

1. Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.

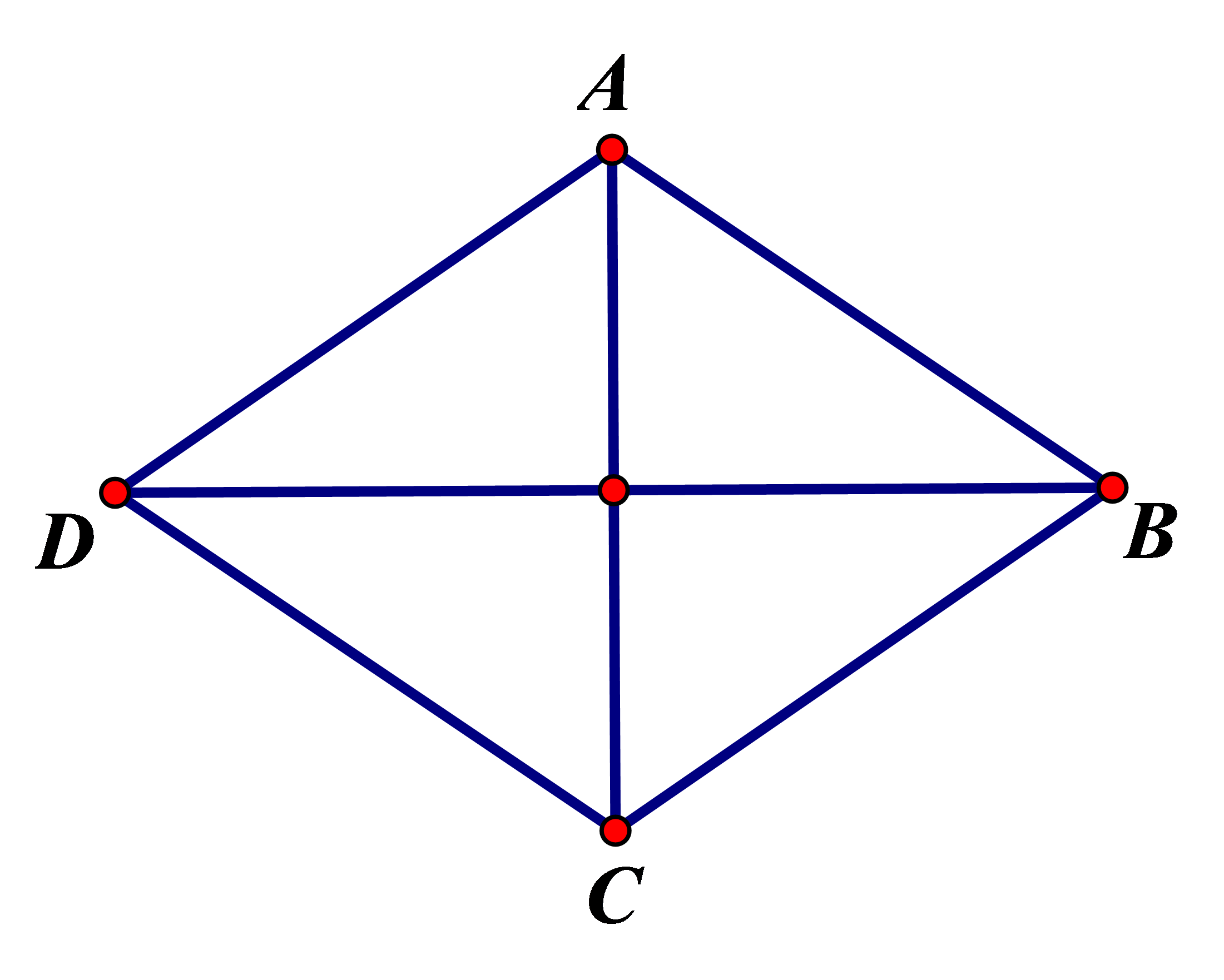
ABCD là hình thoi$\iff$ AB = BC = CD = DA.

Nhận xét: Hình thoi cũng là một hình bình hành.

2. Tính chất:

- Hình thoi có tất cả các tính chất của hình bình hành.

- Trong hình thoi:

a) Hai đường chéo vuông góc với nhau;

b) Hai đường chéo là đường phân giác của các góc ở đỉnh của hình thoi.

3. Dấu hiệu nhận biết:

a) Tứ giác có bốn cạnh bằng nhau là hình thoi;

b) Hình bình hành có hai cạnh kề bằng nhau là hình thoi;

c) Hình bình hành có hai đường chéo vuông góc là hình thoi;

d) Hình bình hành có một đường chéo là đường phân giác của một góc ở đỉnh là hình thoi.

II. Các dạng bài tập và phương pháp giải

Dạng 1. Chứng minh tứ giác là hình thoi

Phương pháp giải: Vận dụng các dấu hiệu nhận biết để chứng minh một tứ giác là hình thoi

Ví dụ 1. Cho tứ giác ABCD có AC = BD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác EFGH là hình thoi.

Lời giải

 

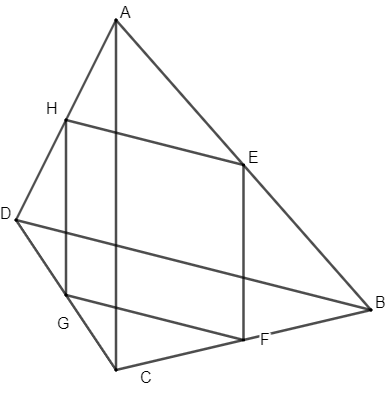
Vì E là trung điểm của AB, F là trung điểm của BC nên EF là đường trung bình của tam giác ABC

$\Rightarrow \left\{\begin{array}{l}\text{EF//AC}\\ \text{EF}=\frac{1}{2}AC\end{array}\right.$(1)

Vì G là trung điểm của DC, H là trung điểm của DA nên HG là đường trung bình của tam giác ADC

$\Rightarrow \left\{\begin{array}{l}\text{HG//AC}\\ HG=\frac{1}{2}AC\end{array}\right.$(2)

Từ (1) và (2)$\Rightarrow \left\{\begin{array}{l}\text{HG//EF}\\ HG=\text{EF}\end{array}\right.$

$\Rightarrow$Tứ giác EFGH là hình bình hành.

Lại có G là trung điểm của DC, F là trung điểm của BC nên GF là đường trung bình của tam giác BCD.

$\Rightarrow GF=\frac{1}{2}BD$

Mà BD = AC

Nên GF = EF

Hình bình hành có hai cạnh kề bằng nhau là hình thoi nên tứ giác EFGH là hình thoi.

Dạng 2. Vận dụng tính chất của hình thoi để chứng minh các tính chất hình học

Phương pháp giải: Vận dụng định nghĩa và các tính chất về cạnh, góc và đường chéo của hình thoi

Ví dụ: Cho hình thoi ABCD có $\widehat{B}={60}^o$. Kẻ $AE\perp DC,$$AF\perp BC$

a) Chứng minh AE = AF;

b) Chứng minh tam giác AEF đều.

Lời giải:

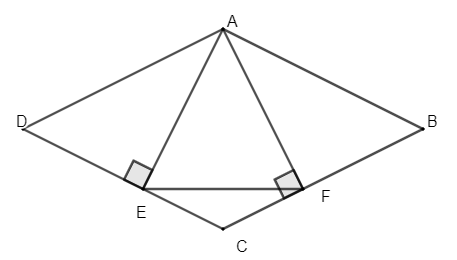
a) Vì ABCD là hình thoi nên ta có:

$\left\{\begin{array}{l}\widehat{ADE}=\widehat{ABF}\\ AD=AB\end{array}\right.$(tính chất)

Lại có:

$\left\{\begin{array}{l}AE\perp CD\Rightarrow \widehat{AED}=90°\\ AF\perp BC\Rightarrow \widehat{A\text{}FB}=90°\end{array}\right.$

Xét tam giác ADE và tam giác ABF có:

$\left\{\begin{array}{l}\widehat{ADE}=\widehat{ABF}\\ AD=AB\\ \widehat{AED}=\widehat{BFA}=90°\end{array}\right.$

$\Rightarrow \Delta ADE=\Delta ABF$ (cạnh huyền – góc nhọn)

$\Rightarrow$AE = AF (hai cạnh tương ứng)

b) Xét $\Delta ABF$ vuông tại F ta có:

$\widehat{BFA}+\widehat{ABF}+\widehat{FAB}=180°$

$\iff 90°+60°+\widehat{FAB}=180°$

$\iff \widehat{FAB}=30°$

Xét $\Delta ADE$ vuông tại E ta có:

$\widehat{DEA}+\widehat{ADE}+\widehat{EAD}=180°$

$\iff 90°+60°+\widehat{EAD}=180°$

$\iff \widehat{EAD}=30°$

Ta có: ABCD là hình thoi nên AD // BC$\Rightarrow \widehat{\text{DA}B}+\widehat{B}=180°$(hai góc trong cùng phía)

Nên $\widehat{DAB}=180°-\widehat{B}$$=180°-60°=120°$

Lại có:$\widehat{DAB}=$$\widehat{DAE}+\widehat{EAF}+\widehat{FAB}$$=120°$

$30°+\widehat{EAF}+30°=120°$

$\Rightarrow \widehat{EAF}=60°$

Xét $\Delta AEF$ có:

AE = AF

$\widehat{EAF}=60°$

Do đó: $\Delta AEF$ là tam giác đều.

Dạng 3. Tìm điều kiện để tứ giác là hình thoi

Phương pháp giải: Vận dụng định nghĩa, các tính chất và dấu hiệu nhận biết của hình thoi

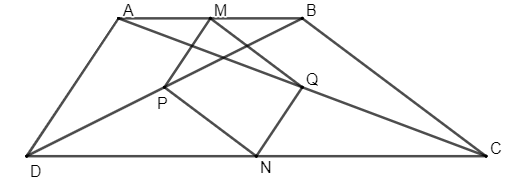
Ví dụ: Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AB, CD, BD, AC.

a) Chứng minh tứ giác MPNQ là hình bình hành;

b) Hình thang ABCD phải có thêm điều kiện gì để tứ giác MPNQ là hình thoi?

Lời giải:

a) Vì M là trung điểm của AB, P là trung điểm của BD nên MP là đường trung bình của tam giác ABD

$\Rightarrow \left\{\begin{array}{l}MP//AD\\ MP=\frac{1}{2}AD\end{array}\right.$(1)

Vì Q là trung điểm của AC, N là trung điểm của DC nên QN là đường trung bình của tam giác ACD

$\Rightarrow \left\{\begin{array}{l}NQ//AD\\ NQ=\frac{1}{2}AD\end{array}\right.$(2)

Từ (1) và (2)$\Rightarrow \left\{\begin{array}{l}NQ//MP\\ NQ=MP\end{array}\right.$

Xét tứ giác MPNQ có:

NQ // MP

Do đó: tứ giác MPNQ là hình bình hành.

b) Để hình bình hành MPNQ là hình thoi thì MP = MQ

Vì M là trung điểm của AB, Q là trung điểm của AC nên MQ là đường trung bình của tam giác ABC

$\Rightarrow MQ=\frac{1}{2}BC$

Để MQ = MP thì $\frac{1}{2}BC=\frac{1}{2}AD$ hay BC = AD

Vậy để MPNQ là hình thoi thì hình thang ABCD phải có hai cạnh bên AD và BC bằng nhau.

III. Bài tập tự luyện

1.Bài tập vận dụng

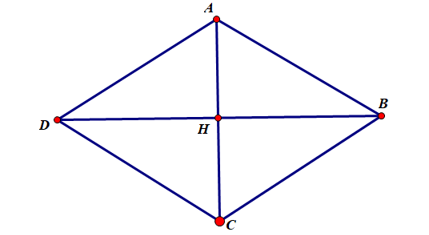
Bài 1. Cho hình thoi có độ dài hai đường chéo là 24 cm và 10 cm. Tính độ dài cạnh hình thoi.

Hướng dẫn giải

Giả sử hình thoi có hai đường chéo cắt nhau tại H và AC = 10 cm, BD = 24 cm.

Do ABCD là hình thoi nên:

AC ⊥ BD

$AH=\frac{1}{2}AC=\frac{1}{2}.10=5\left(cm\right)$

$HB=\frac{1}{2}BD=\frac{1}{2}.24=12\left(cm\right)$

Xét tam giác AHB vuông tại H:

AB² = AH² + HB² = 5² + 12² = 169

Do đó AB = 13 cm.

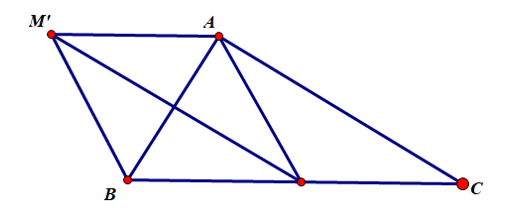
Bài 2. Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D. Tứ giác AMBM’ là hình gì?

Hướng dẫn giải

 

Vì M’ đối xứng M qua D nên DM = DM’

M là trung điểm BC

D là trung điểm AB

Suy ra MD là đường trung bình của ΔABC.

Suy ra MD // AC.

Mặt khác ΔABC vuông ở A nên AB ⊥ AC.

Do đó AB ⊥ DM hay AB ⊥ MM’.

Vì D là trung điểm của AB và MM’ nên tứ giác AMBM’ là hình bình hành.

Mà AB ⊥ MM’ nên AMBM’ là hình thoi.

Vậy AMBM’ là hình thoi.

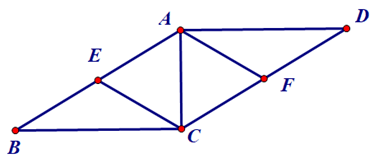
Bài 3. Cho hình bình hành ABCD có AC vuông góc với AD. Gọi E, F theo thứ tự là trung điểm của các cạnh AB, CD. Chứng minh tứ giác AECF là hình thoi.

Hướng dẫn giải

Vì hình bình hành ABCD có AC vuông góc với ADnên $\widehat{CAD}=\widehat{ACB}=90°$.

Xét tam giác vuông CAD vuông tại A có AF là đường trung tuyến ứng với cạnh huyền CD.

Suy ra $AF=\frac{1}{2}CD\Rightarrow AF=FC=FD=\frac{1}{2}CD$  (1)

Tương tự xét tam giác vuông ACB vuông tại C có CE là đường trung tuyến ứng với cạnh huyền AB.

 $\Rightarrow CE=\frac{1}{2}AB\Rightarrow EC=AE=EB=\frac{1}{2}AB$(2)

Lại có: AB = CD (tính chất hình bình hành) (3)

Từ (1), (2) và (3) suy ra AE = CE = CF = FA

Suy ra tứ giác AECF là hình thoi.

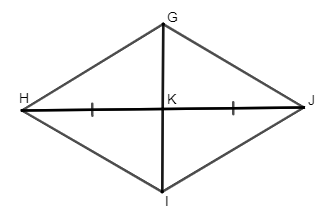
Bài 4. Cho tam giác GHJ cân tại G. Đường trung tuyến kẻ từ G của tam giác cắt HJ tại K. Lấy điểm I trên tia GK sao cho KG = KI. Chứng minh GHIJ là hình thoi.

Hướng dẫn giải

• Ta có GK là trung tuyến của tam giác GHJ nên K là trung điểm của HJ.

Do KG = KI nên K là trung điểm của GI.

Tứ giác GHIJ có hai đường chéo GI và HJ cắt nhau tại trung điểm K của mỗi đường nên là hình bình hành.

• ∆GHJ cân tại G nên đường trung tuyến GK đồng thời là đường cao tương ứng với cạnh HJ nên GI ⊥ HJ.

Hình bình hành GHIJ có hai đường chéo GI và HJ vuông góc với nhau nên là hình thoi

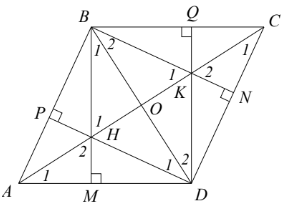
Bài 5. Cho hình thoi ABCD có B là góc tù. Từ B hạ BM ⊥ AD, BN ⊥ CD. Từ D hạ DP ⊥ AB, DQ ⊥ BC. Gọi H là giao điểm của MB và PD, K là giao điểm của BN và DQ, O là giao điểm của AC và BD.

a) Chứng minh H là trực tâm của tam giác ABD.

b) Chứng minh A, H, K, C thẳng hàng.

c) Chứng minh $\widehat{PDQ}=\widehat{MBN}$ .

d) Chứng minh $\widehat{PHM}=\widehat{QKN}$ .

e) Chứng minh tứ giác BHDK là hình thoi.

Hướng dẫn giải

a) Tam giác ABD có hai đường cao BM, DP cắt nhau tại H nên H là trực tâm của tam giác.

b) ABCD là hình thoi nên AC ⊥ BD tại O, do đó A, O, C thẳng hàng (1)

Do H là trực tâm của DABD suy ra AH ⊥ BD tại O nên H ∈ AO (2)

Chứng minh tương tự câu a ta có K là trực tâm DBCD

Suy ra CK ⊥ BD tại O nên K ∈ CO (3)

Từ (1), (2) và (3) suy ra A, H, K, C thẳng hàng.

c) Vì ABCD là hình thoi nên hai đường chéo AC, BD vuông góc với nhau tại trung điểm của mỗi đường

Suy ra AC là đường trung trực của BD

Do đó HB = HD nên DHBD cân tại H, suy ra ${\hat{B}}_1={\hat{D}}_1$

Tương tự, ${\hat{B}}_2={\hat{D}}_2$

Suy ra ${\hat{B}}_1+{\hat{B}}_2={\hat{D}}_1+{\hat{D}}_2$ hay $\widehat{MBN}=\widehat{PDQ}$.

d) ABCD là hình thoi nên $\widehat{BAD}=\widehat{BCD}$

Tứ giác APHM có $\widehat{PHM}=360°-90°-90°-\widehat{BAD}$

Tứ giác CQKN có $\widehat{QKN}=360°-90°-90°-\widehat{BCD}$

Suy ra $\widehat{PHM}=\widehat{QKN}$ .

e) Ta có: ${\hat{A}}_1+{\hat{H}}_2=90°$ và ${\hat{C}}_1+{\hat{K}}_2=90°$

Mà ${\hat{A}}_1={\hat{C}}_1$ nên ${\hat{H}}_2={\hat{K}}_2$

Lại có ${\hat{H}}_1={\hat{H}}_2$ (đối đỉnh) và ${\hat{K}}_1={\hat{K}}_2$ (đối đỉnh) nên ${\hat{H}}_1={\hat{K}}_1$

Suy ra DBHK cân tại B, nên BH = BK

Mà BH = DH và BK = DK nên BH = HD = CK = KB

Suy ra tứ giác BHDK là hình thoi.

2.Bài tập tự luyện

Bài 1.

a) Cho hình thoi ABCD có hai đường cao AH, AK. Chứng minh AH = AK.

b) Cho hình bình hành ABCD có hai đường cao AH, AK bằng nhau. Chứng minh ABCD là hình thoi.

Bài 2. Hình thoi ABCD có $\widehat{A}={60}^o$. Kẻ hai đường cao BE, BF. Tam giác BEF là tam giác gì? Vì sao?

Bài 3. Cho tam giác ABC, phân giác AD. Qua D kẻ đường thẳng song song với AC cắt AB tại E, qua D kẻ đường thẳng song song với AB cắt AC tại F. Chứng minh EF là phân giác của góc AED.

Bài 4. Cho hình chữ nhật ABCD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA.

a) EFGH là hình gì? Vì sao?

b) Chứng minh AC, BD, EG, FH đồng quy.

Bài 5. Cho tam giác ABC cân tại A, trung tuyến AM. Qua M kẻ đường thẳng song song với AC cắt AB tại P và đường thẳng song song với AB cắt AC tại Q.

a) Tứ giác APMQ là hình gì? Vì sao?

b) Chứng minh PQ // BC.

Bài 6. Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.

a) Chứng minh E và F đối xứng nhau qua AB;

b) Chứng minh tứ giác MEBF là hình thoi;

c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.

Bài 7. Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H lần lượt là chân các đường vuông góc kẻ từ O đến AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Bài 8. Hình thoi ABCD có $\widehat{A}={60}^o$. Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì? Vì sao?

Bài 9. Dựng hình thoi ABCD biết cạnh bằng 2cm, một đường chéo bằng 3cm.

Bài 10. Cho tam giác ABC. Lấy các điểm D, E theo thứ tự trên các cạnh AB, AC sao cho BD = CE. Gọi M, N, I, K theo thứ tự là trung điểm của BE, CD, DE, BC. Chứng minh $IK\perp MN$.

Bài 11. Cho tam giác ABC nhọn, các đường cao BD, CE. Tia phân giác của các góc ABD và ACE cắt nhau tại O và lần lượt cắt AC, BD tại N, M. Tia BN cắt CE tại K, tia CM cắt BD tại H. Chứng minh:

a) $BN\perp CM$;

b) Tứ giác MNHK là hình thoi.

Bài 12. Cho tứ giác ABCD có AD = BC. Gọi I, J lần lượt là trung điểm của các cạnh AB và CD; K, H theo thứ tự là trung điểm của hai đường chéo AC và BD. Chứng minh rằng: IJ$\perp$HK

Bài 13. Cho hình bình hành ABCD có AB = 2BC. Gọi M, N lần lượt là trung điểm của AB và CD.

a) Chứng minh tứ giác AMND là hình thoi.

b) Gọi E là giao điểm của AN và DM; F là giao điểm của BN và MC. Tứ giác MENF là hình gì? Vì sao?

Bài 14. Cho hình thoi ABCD có AB = AC.

Kẻ $AE\perp BC$ $\left(E\in BC\right);$ $AF\perp CD(F\in CD)$

a) Chứng minh $\Delta AEF$ đều.

b) Biết AB = 4cm. Tính độ dài các đường chéo của hình thoi.

Bài 15. Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE. Tia phân giác của góc DAC cắt BE, BC theo thứ tự tại I và K. Tia phân giác của góc EBC cắt AB, AC tại M và N. Chứng minh tứ giác MINK là hình thoi.

Bài 16. Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E, F, G, H theo thứ tự là giao điểm của các đường phân giác của các tam giác AOB, BOC, COD, DOA. Chứng minh EFGH là hình thoi.

Bài 17. Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng song song với AB, AC cắt AC, AB theo thứ tự tại E và F.

a) Tứ giác AEDF là hình gì?

b) Điểm D ở vị trí nào trên BC thì AEDF là hình thoi?

Xem thêm các dạng bài tập hay, có đáp án:

50 Bài tập về hình chữ nhật. hình thoi. hình bình hành. hình thang cân (có đáp án năm 2024) - Toán 6

20 bài tập về Hình chữ nhật, Hình thoi, Hình bình hành, Hình thang cân (2024) có đáp án, chi tiết nhất

60 Bài tập về Hình thoi. Diện tích hình thoi (có đáp án năm 2024) - Toán lớp 4

Cách tính chu vi và diện tích hình thoi (2024) đầy đủ, chi tiết nhất

50 Bài tập Hình nón – Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt (có đáp án năm 2024) - Toán 9