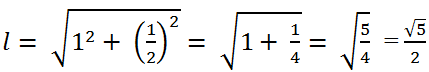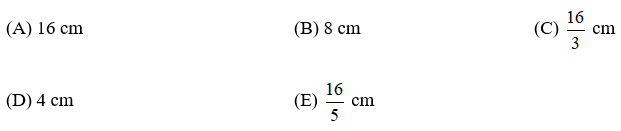Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Kiến thức cần nhớ
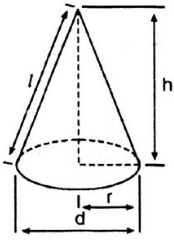
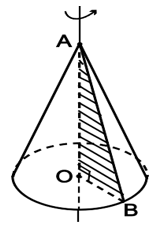
1. Hình nón
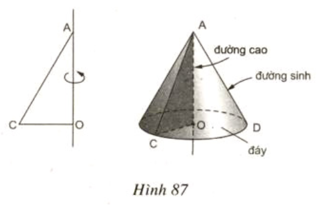
Khi quay tam giác vuông AOC một vòng quanh cạnh OA cố định thì được một hình nón.
- Điểm A được gọi đỉnh của hình nón.
- Hình tròn (O) được gọi là đáy của hình nón.
- Mỗi vị trí của AC được gọi là một đường sinh của hình nón.
- Đoạn AO được gọi là đường cao của hình nón.
2. Diện tích và thể tích của hình nón
Đặt AC = l; l là đường sinh.
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
- Diện tích xung quanh: Sxq = πRl.
- Diện tích toàn phần: Stp = πRl + πR2.
- Thể tích: V=13πR2h.
Ví dụ 1. Một hình nón có đường cao bằng 24 cm và thể tích bằng 800π cm3. Tính diện tích toàn phần của hình nón này.
Lời giải:
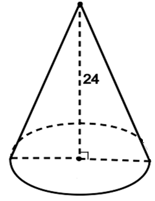
Gọi R là bán kính và h là chiều cao của hình nón.
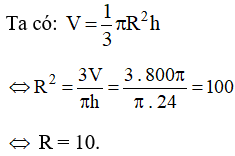
Do đó bán kính của hình nón là 10 cm.
Đường sinh của hình nón là:
SB2=√SO2+OB2=√242+102=26(cm)
Diện tích toàn phần của hình nón là:
Stp = πR(l + R) = π . 10 (26 + 10) = 360π (cm2).
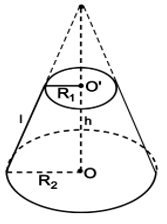
3. Hình nón cụt
Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần hình nón nằm giữa mặt phẳng nói trên và mặt phẳng đáy được gọi là một hình nón cụt.
- Hai hình tròn (O) và (O') được gọi là hai đáy.
- Đoạn OO' được gọi là trục. Độ dài OO' là chiều cao.
- Đoạn AC được gọi là đường sinh.
4. Diện tích và thể tích hình nón cụt
Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.
- Diện tích xung quanh: Sxq = π (R + r) l.
- Thể tích: V=13πh(R2+Rr+r2).
Ví dụ 2. Một hình nón đỉnh S có bán kính đáy bằng 9 cm và chiều cao SO = 21,6 cm. Cắt hình nón bởi một mặt phẳng song song với đáy tạo ra một hình nón cụt có chiều cao 12 cm. Tính diện tích xung quanh của hình nón cụt.
Lời giải:
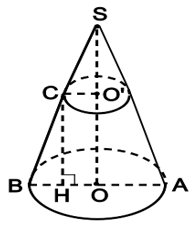
Xét mặt cắt qua trục của hình nón là ∆SAB cân tại S.
Trong mặt phẳng SAB có O’C // OB.
Theo định lý Ta – lét ta có O'.
Do đó O’C = 4 (cm).
Trong mặt phẳng SAB vẽ , ta được:
CH = OO’ = 12 cm, BH = 9 – 4 = 5 (cm).
Suy ra BC = (cm)
Diện tích xung quanh của hình nón cụt là:
Sxq = π(R1 + R2)l = π(9 + 4) . 13 = 169π (cm2)
Vậy diện tích xung quanh của hình nón cụt là 169π cm2.
Bài tập tự luyện (có đáp án)
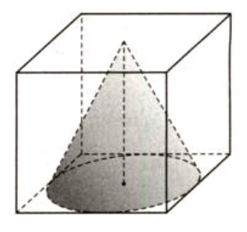
Bài 1: Một hình nón được đặt vào bên trong một hình lập phương như hình vẽ (cạnh của hình lập phương bằng 1) (h.93). Hãy tính:
a) Bán kính đáy của hình nón.
b) Độ dài đường sinh.
Hình 93
Lời giải
a) Ta có đường tròn đáy của hình nón nội tiếp trong hình vuông của một mặt của hình lập phương. Do đo bán kính của hình tròn đáy của hình nón bằng một nửa của cạnh hình lập phương và bằng 0,5.
b) Đỉnh của hình nón tiếp xúc với một mặt của hình lập phương nên đường cao của hình nón bằng với cạnh của hình lập phương và bằng 1.
Theo định lí Pitago, độ dài đường sinh của hình nón là:
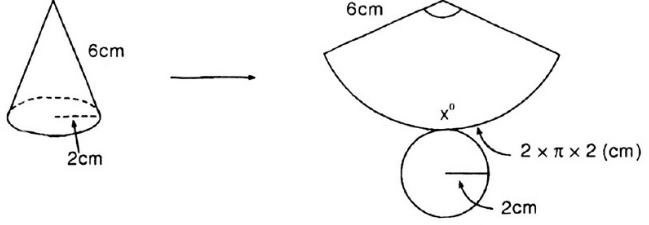
Bài 2: Cắt mặt cắt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết bán kính hình quạt tròn bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.
Quan sát hình 94 và tính số đo cung của hình quạt tròn.
Hình 94
Lời giải
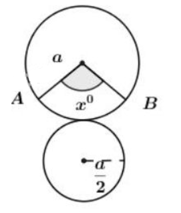
Bài 3: Khi quay tam giác vuông để tạo ra một hình nón như hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là 30°, độ dài đường sinh là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
Lời giải
Theo đề bài ta có: nên góc ở đỉnh của hình nón là , suy ra đường kính của đường tròn đáy của hình nón bằng a (do tam giác ABC đều).
Vậy bán kính đáy của hình nón là:
Chu vi đáy hình nón là:
Đường sinh của hình nón là AC = a (do tam giác ABC đều)
Khai triển mặt xung quanh hình nón ta được hình quạt AOB có bán kính R = a
Gọi số đo cung AB là x°, độ dài cung AB là:
Mặt khác, độ dài cung AB bằng chu vi đáy hình nón nên ta có:
Vậy số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón là 180°.
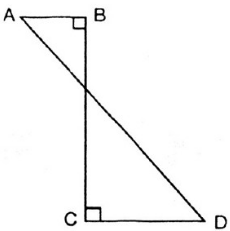
Bài 4: Hình ABCD (h.95) khi quay quanh BC thì tạo ra:
(A) Một hình trụ
(B) Một hình nón
(C) Một hình nón cụt
(D) Hai hình nón
(E) Hai hình trụ
Hãy chọn câu trả lời đúng.
Hình 95
Lời giải
Nếu gọi O là giao điểm của BC và AD. Khi quay hình ABCD quanh BC thì có nghĩa là quay tam giác vuông OAB quanh OB và tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ là hai hình nón.
Vậy chọn D.
Bài 5: Hình khai triển của mặt xung quanh của một hình nón là một hình quạt. Nếu bán kính hình quạt là 16cm, số đo cung là 1200 thì độ dài đường sinh của hình nón là:
Lời giải
Khi khai triển mặt xung quanh của hình nón, ta được một hình quạt có bán kính bằng độ dài đường sinh.
Đề bài cho ta bán kính hình tròn chứa hình quạt là 16cm nên độ dài đường sinh của hình nón là 16cm.
Vậy chọn A.
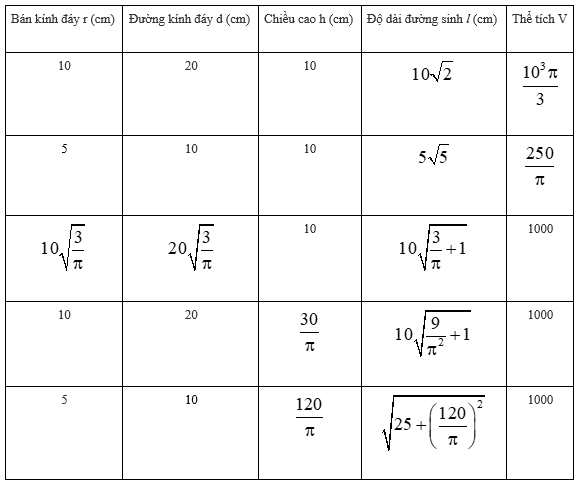
Bài 6: Hãy điền đủ vào các ô trống ở bảng sau (xem hình 96):
| Bán kính đáy r(cm) | Đường kính đáy d(cm) | Chiều cao h(cm) | Độ dài đường sinh l(cm) | Thể tích V |
| 10 | 10 | |||
| 10 | 10 | |||
| 10 | 1000 | |||
| 10 | 1000 | |||
| 1000 |
Hình 96
Lời giải
Cách tính:
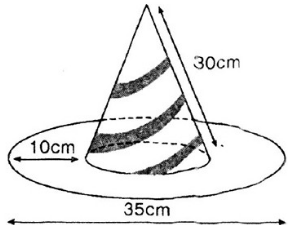
Bài 7: Cái mũ của chú hề với các kích thước cho theo hình vẽ (h.97). Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa).
Hình 97
Lời giải
Diện tích vải cần có để làm nên cái mũ gồm diện tích xung quanh của hình nón và diện tích của vành nón.
Bán kính đường tròn đáy của hình nón:
Diện tích xung quanh hình nón: Sxq = π.r.l = π.7,5.30 = 225π (cm2)
Diện tích vành nón (hình vành khăn):
Diện tích vải cần để may: 225π + 250π = 475π ≈ 1492,3 (cm2).
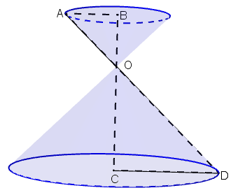
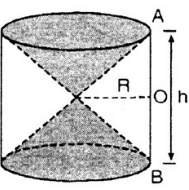
Bài 8: Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (AO = OB).
Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.
Hình 98
Lời giải
Xem thêm các dạng bài tập liên quan khác:
50 Bài tập Hình cầu. Diện tích mặt cầu và thể tích hình cầu (2024) có đáp án
50 Bài tập Ôn tập chương 4: Hình Trụ - Hình Nón - Hình Cầu (có đáp án năm 2024)
50 Bài tập Hình trụ - Diện tích xung quanh và thể tích của hình trụ (có đáp án năm 2024)
50 Bài tập Diện tích hình tròn, hình quạt tròn (có đáp án năm 2024)
50 Bài tập Độ dài đường tròn, cung tròn (có đáp án năm 2024)