Cách tính chu vi và diện tích hình thoi (2024) đầy đủ, chi tiết nhất

Cách tính chu vi và diện tích hình thoi

I. Phương pháp giải

1. Hình thoi là gì?

Hình thoi là tứ giác có bốn cạnh bằng nhau hay là hình bình hành có hai đường chéo vuông góc với nhau, có hai cạnh bên bằng nhau, có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường đồng thời là đường phân giác của mỗi góc.

Trong trường hợp hình thoi có bốn góc vuông trong bằng nhau thì hình thoi được xác định là hình vuông. Như vậy, hình vuông là một trường hợp đặc biệt của hình thoi vì nó có bốn cạnh dài bằng nhau và có bốn góc vuông.

Tất cả các hình vuông đều là hình thoi nhưng không phải mọi hình thoi đều là hình vuông.

2. Tính chất của hình thoi

Thứ nhất, hình thoi có đầy đủ tính chất của hình bình hành: các cạnh đối song song với nhau và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Thứ hai, hình thoi có các góc đối bằng nhau, tổng các góc trong hình thoi bằng 360 độ.

Thứ ba, hình thoi có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường.

Thứ tư, hình thoi có hai đường chéo là đường phân giác của các góc trong hình thoi.

3. Dấu hiệu nhận biết của hình thoi

Dấu hiệu 1: Hình thoi là tứ giác có 4 cạnh bằng nhau

Dấu hiệu 2: Hình thoi là tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường hình thoi

Dấu hiệu 3: Hình thoi là hình bình hành có hai cạnh kề bằng nhau

Dấu hiệu 4: Hình thoi là hình bình hành có hai đường chéo vuông góc với nhau

Dấu hiệu 5: Hình thoi là hình bình hành có đường chéo là đường phân giác của một góc

4. Công thức tính chu vi của hình thoi

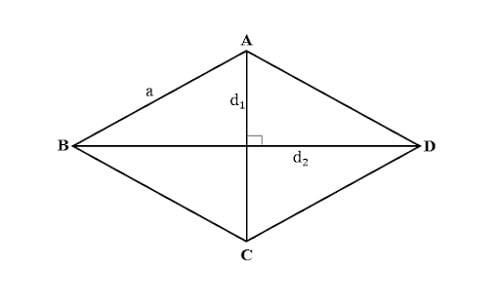
Muốn tính chu vi hình thoi, ta lấy tổng độ dài của các cạnh hoặc độ dài một cạnh nhân với 4. Công thức tính chu vi hình thoi như sau:

P = a + a + a + a = a x 4

Trong đó: P là chu vi hình thoi, a là chiều dài của cạnh hình thoi

Ví dụ: Cho một hình thoi ABCD có độ dài các cạnh bằng nhau và bằng 4 cm. Hỏi chu vi của hình thoi bằng bao nhiêu?

Áp dụng công thức tính chu vi hình thoi, có cạnh a = 4 cm.

Giải:

Chu vi của hình thoi ABCD là:  

4 x 4 = 16 (cm)

Đáp số: 16 (cm)

5. Công thức tính diện tích của hình thoi

Diện tích hình thoi bằng một nửa tích độ dài của hai đường chéo. Đường chéo của hình thoi là đường thẳng nối các đỉnh đối diện với nhau (hai đường chéo của hình thoi sẽ vuông góc với nhau và cắt nhau tại một điểm). Ta có công thức tính diện tích hình thoi như sau:

S = 1/2 x (d1 x d2)

Trong đó: S là diện tích hình thoi, d1 là đường chéo d1, d2 là đường chéo d2

Ví dụ: Cho hình thoi ABCD có độ dài hai đường chéo lần lượt là 6 cm và 10 cm. Tình diện tích hình thoi ABCD?

Giải:

Diện tích của hình thoi ABCD là:

6 x 10 : 2 = 30 (cm²)

Đáp số: 30 (cm²)

Ngoài công thức trên, ta còn có một số cách khác để tính diện tích hình thoi như:

Thứ nhất, công thức tính diện tích hình thoi dựa vào hệ thức trong tam giác (trong trường hợp biết được số đo góc của hình thoi)

S = a² . sin A = a² . sin B = a² . sin C = a² . sin D

Ví dụ: Cho hình thoi ABCD có cạnh hình thoi là 4 cm và góc A có số đo là 30°. Tính diện tích của hình thoi ABCD?.

Giải:

* Cách 1:

Diện tích của hình thoi ABCD là:

S = a² . sin A = 4² . sin30° = 16 . 1/2 = 8 (cm²)

Vậy diện tích của hình thoi ABCD là 8 cm².

* Cách 2:

Vì ABCD là hình thoi nên các tam giác tạo thành là tam giác cân.

Gọi O là giao điểm của hai đường chéo AC, BD và O cũng là trung điểm của hai đường chéo này nên AO vuông góc với BD. Do đó, góc BAO = 1/2 góc BAD = 15°.

Nên: AO = AB . cos BAO = 4 . cos15° = 3,84 (cm)

Áp dụng định lý Py-ta-go vào tam giác AOB ta được:

AB² = AO² + OB² ⇔ OB² = AB² - AO² = 4² - 3,84² = 1,25

⇒ OB = 1,1 (cm)

Từ đó: AC = 2 . AO = 2 . 3,84 = 7,68 (cm) và BD = 2 . OB = 2 . 1,1 = 2,2 (cm)

Diện tích của hình thoi ABCD là: S = 1/2 . AC . BD = 1/2 . 7,68 . 2,2 = 8,45 (cm²)

Vậy diện tích của hình thoi ABCD là 8,45 (cm²)

Thứ hai, công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao.

S = h x a

Trong đó: S là diện tích hình thoi, h là chiều cao của hình thoi, a là cạnh đáy

Ví dụ: Cho hình thoi ABCD có cạnh AB = BC = CD = DA = 5 (cm), chiều cao của hình thoi bằng 4 cm. Tính diện tích của hình thoi.

Giải:

Áp dung công thức tính diện tích hình thoi có: h = 4 (cm), a = 5 (cm) ta được:

S = a x h = 5 x 4 = 20 (cm²)

Vậy diện tích của hình thoi ABCD là 20 (cm²)

6. Một số ví dụ áp dụng công thức tính chu vi và tính diện tích của hình thoi

Ví dụ 1: Một khu đất hình thoi có tổng độ dài hai đường chéo là 400 cm. Biết độ dài đường chéo thứ nhất bằng 3/5 độ dài đường chéo thứ hai. Tính diện tích khu đất hình thoi đó?

Giải:

Tổng số phần bằng nhau là: 3 + 5 = 8 (phần)

Độ dài đường chéo thứ hai là: 400 : 8 x 5 = 250 (cm)

Độ dài đường chéo thứ nhất là: 400 - 250 = 150 (cm)

Diện tích của hình thoi là: 250 x 150 : 2 = 18750 (cm²)

Đáp số: 18750 (cm²)

Ví dụ 2: Một khu đất hình thoi có độ dài đường chéo thứ nhất là 20 m, đường chéo thứ hai có độ dài bằng 3/4 độ dài đường chéo thứ nhất. Bác nông dân có trồng khoai tây trên khu đất này và được biết mỗi mét vuông đất thì thu hoạch được 5kg. Hỏi bác nông dân thu hoạch được bao nhiêu ki-lô-gam khoai tây?

Giải:

Độ dài đường chéo thứ hai là: 20 : 4 x 3 = 15 (m)

Diện tích của khu đất hình thoi là: 20 x 15 : 2 = 150 (m²)

Số khoai tây thu hoạch được trên khu đất là: 150 x 5 = 750 (kg)

Đáp số: 750 kg khoai tây

Ví dụ 3: Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Được biết diện tích hình thoi là 60 cm² và AC = 10 cm. Tính độ dài cạnh của hình thoi?

Giải:

Diện tích của hình thoi là:

S = 1/2 . AC . BD ⇒ BD = (2.S)/AC = (2 . 60) / 10 = 12 (cm)

Theo tính chất của hình thoi ta có: O là trung điểm của AC và BD

nên: OA = 1/2 . AC = 1/2 . 10 = 5 (cm) và OB = 1/2 . BD = 1/2 . 12 = 6 (cm)

Áp dụng định lý Py-ta-go vào tam giác AOB ta có:

AB² = OA² + OB² = 5² + 6² = 61, suy ra: AB = 7,81 (cm)

Vậy độ dài cạnh của hình thoi là: 7,81 cm

II.Bài tập 

a. Bài tập vận dụng

Bài 1: Tính diện tích của hình thoi biết độ dài hai đường chéo lần lượt là 16cm và 20cm.

Bài 2: Một hình thoi có độ dài đường chéo lớn là 12dm, diện tích hình thoi là 48dm². Tính độ dài đường chéo còn lại của hình thoi.

Bài 3: Hình thoi ABCD có độ dài đường chéo AC = 15cm, độ dài đường chéo BD bằng 2/3 độ dài đường chéo AC. Tính diện tích hình thoi ABCD.

Bài 4: Tính diện tích hình thoi MNPQ biết cạnh AB = 22cm và cạnh AD = 17cm.

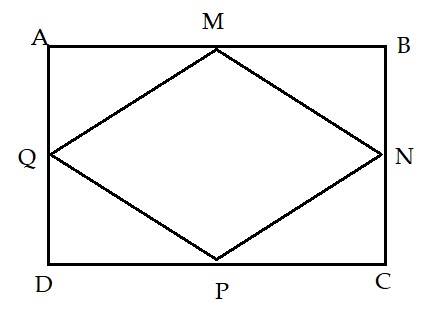
Bài 5: Cho hình thoi có diện tích bằng diện tích hình vuông cạnh 10cm, biết 1 đường chéo hình thoi bằng độ dài cạnh hình vuông. Tính độ dài đường chéo còn lại của hình thoi.

Bài 6: Tỉ số giữa hai đường chéo một hình thoi là 4/9. Hiệu của hai đường chéo là 20m. Tính diện tích của hình thoi?

Bài 7: Một hình thoi có tổng độ dài hai đường chéo là 270cm, biết độ dài đường chéo ngắn bằng 4/5 độ dài đường chéo dài. Tính diện tích hình thoi.

Bài 8: Một khu đất hình thoi có độ dài đường chéo thứ nhất là 72m, đường chéo thứ hai có độ dài bằng 2/3 độ dài đường chéo thứ nhất. Người ta trồng sắn trên khu đấy, mỗi mét vuông thu hoạch được 5kg sắn. Hỏi người ta thu hoạch được ở khu đất bao nhiêu ki-lô-gam sắn?

Bài 9: Người ta trồng rau trên một thửa ruộng hình thoi có tổng độ dài hai đường chéo là 50m và đường chéo thứ nhất dài hơn đường chéo thứ hai 10m. Trên thửa ruộng đó người ta thu hoạch được 100kg rau. Hỏi trung bình mỗi mét vuông đất người ta thu hoạch được bao nhiêu ki-lô-gam rau?

Bài 10: Một tấm gỗ hình chữ nhật có chu vi là 40cm, chiều rộng bằng 2/3 chiều dài. Người ta cắt và ghép tấm gỗ thành hình thoi. Tính diện tích hình thoi đó.

 Lời giải bài tập hình thoi

Bài 1:

Diện tích của hình thoi là:

16 x 20 : 2 = 160 (cm²)

Đáp số: 160cm²

Bài 2:

Độ dài đường chéo còn lại của hình thoi là:

48 x 2 : 12 = 8(dm)

Đáp số: 8dm

Bài 3:

Độ dài đường chéo BD là:

15 : 3 x 2 = 10 (cm)

Diện tích hình thoi ABCD là:

15 x 10 : 2 = 75(cm²)

Đáp số: 75cm²

Bài 4:

Diện tích hình thoi MNPQ là:

17 x 22 : 2 = 187(cm²)

Đáp số: 187cm²

Bài 5:

Diện tích của hình vuông hay diện tích của hình thoi là:

10 x 10 = 100(cm²)

Độ dài đường chéo còn lại của hình thoi là:

100 x 2 : 10 = 20(cm)

Đáp số: 20cm

Bài 6:

Hiệu số phần bằng nhau là:

9 – 4 = 5 (phần)

Độ dài đường chéo thứ nhất là:

20 : 5 x 4 = 16(m)

Độ dài đường chéo thứ hai là:

16 + 20 = 36(m)

Diện tích của hình thoi là:

16 x 36 : 2 = 288(m²)

Đáp số: 288m²

Bài 7:

Tổng số phần bằng nhau là:

4 + 5 = 9 (phần)

Độ dài đường chéo dài là:

270 : 9 x 5 = 150(cm)

Độ dài đường chéo ngắn là:

270 – 150 = 120(cm)

Diện tích của hình thoi là:

150 x 120 : 2 = 9000(cm²)

Đáp số: 9000cm²

Bài 8:

Độ dài đường chéo thứ hai là:

72 : 3 x 2 = 48(m)

Diện tích của khu đất hình thoi là:

72 x 48 : 2 = 1728(m²)

Số sắn thu hoạch được trên khu đất là:

5 x 1728 = 8640(kg)

Đáp số: 8640kg sắn

Bài 9:

Độ dài đường chéo thứ nhất là:

(50 + 10) : 2 = 30(m)

Độ dài đường chéo thứ hai là:

30 – 10 = 20 (m)

Diện tích thửa ruộng hình thoi là:

30 x 20 : 2 = 300(m²)

Trung bình mỗi mét vuông đất người ta thu hoạch được số ki-lô-gam rau là:

300 : 100 = 3(kg)

Đáp số: 3kg rau

Bài 10:

Nửa chu vi của tấm gỗ hình chữ nhật là:

40 : 2 = 20 (cm)

Tổng số phần bằng nhau là:

2 + 3 = 5 (phần)

Chiều dài của tấm gỗ hình chữ nhật là:

20 : 5 x 3 = 12 (cm)

Chiều rộng của tấm gỗ hình chữ nhật là:

20 – 12 = 8(cm)

Diện tích của hình thoi là:

12 x 8 : 2 = 48(cm²)

Đáp số: 48cm²

 b.Bài tập tự luyện tính diện tích, chu vi hình thoi

Bài 1: Một hình thoi có diện tích 4dm², độ dài đường chéo là 3/5 dm. Tính độ dài của đường chéo thứ hai.

Bài 2: Tính diện tích hình thoi biết đường chéo thứ nhất bằng 45cm, đường chéo thứ hai bằng 3/5 đường chéo thứ nhất.

Bài 3: 

1) Diện tích hình thoi 250 m², độ dài đường chéo thứ nhất là 25m. Tính độ dài đường chéo thứ hai.

2) Một hình thoi có độ dài trung bình cộng của độ dài 2 đường chéo là 3dm 6cm, độ dài đường chéo lớn gấp đôi độ dài đường chéo bé. Tính diện tích của hình thoi đó?

Bài 4: Một thửa ruộng hình thoi có đường chéo lớn bằng 120 m, độ dài đường chéo bé bằng 3/4 độ dài đường chéo lớn. Người ta cấy lúa trên thửa ruộng đó, cứ 1 m² thu hoạch được 2 kg thóc. Hỏi trên thửa ruộng đó người ta thu được bao nhiêu tạ thóc?

Bài 5: Một thửa ruộng hình thoi có tổng độ dài 2 đường chéo là 28m và hiệu độ dài 2 đường chéo là 12m. Tính diện tích thửa ruộng đó?

Bài 6: Tính diện tích hình thoi biết độ dài hai đường chéo lần lượt là:

a) 3m 8dm và 5m

b) 4m 3cm và 60dm

Bài 7: Tính chu vi hình thoi biết độ dài cạnh của hình thoi là:

a) 5cm	b) 7dm 3cm	c) 12m
d) 5dm 6cm	e) 8m 3dm	g) 4m 6cm

Xem thêm các dạng bài tập hay, có đáp án:

50 Bài tập về hình chữ nhật. hình thoi. hình bình hành. hình thang cân (có đáp án năm 2024)

20 bài tập về Hình chữ nhật, Hình thoi, Hình bình hành, Hình thang cân (2024)

60 Bài tập về Hình thoi. Diện tích hình thoi (có đáp án năm 2024)

50 bài tập về hình thoi (có đáp án 2024)

60 Bài tập về chu vi hình tam giác, hình tứ giác, hình chữ nhật, hình vuông (có đáp án năm 2024