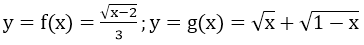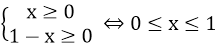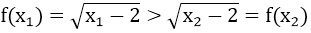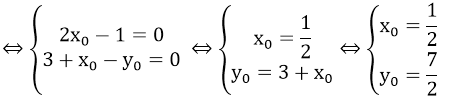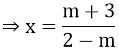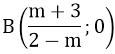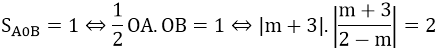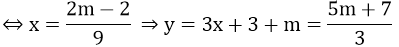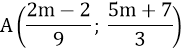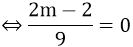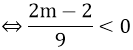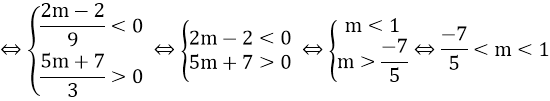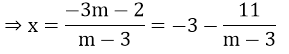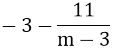50 Bài tập Hàm số bậc nhất
Kiến thức cần nhớ
1. Định nghĩa hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a ≠ 0.
Chú ý: Khi b = 0 ta có hàm số y = ax (đã học ở lớp 7)
Ví dụ 1. Cho các hàm số:
y = 3x; y = x + 2; y = 12x+2;
y = 3x + 1; y = 4x − 1; y = 2 − 3x;
Đây là các hàm số bậc nhất.
2. Tính chất hàm số bậc nhất
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có các tính chất như sau:
• Đồng biến trên R khi a > 0.
• Nghịch biến trên R khi a < 0.
Ví dụ 2. Cho các hàm số sau: y = 4x – 1, y = − 2x + 1, y = 12x+5; y = − √2x. Hàm số nào đồng biến, hàm số nào nghịch biến?
Lời giải:
- Hàm số y = 4x – 1 có a = 4 > 0 nên hàm số này đồng biến trên R.
- Hàm số y = − 2x + 1 có a = − 2 < 0 nên hàm số này nghịch biến trên R.
- Hàm số y = 12x+5 có a = 12 > 0 nên hàm số này đồng biến trên R.
- Hàm số y = − √2x có a = − √2 < 0 nên hàm số này nghịch biến trên R.
Vậy hàm số đồng biến là: y = 4x – 1; y = 12x+5;
Hàm số nghịch biến là: y = − 2x + 1; y = − √2x.
Bài tập tự luyện
Bài 1: Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b của chúng và xét xem hàm số bậc nhất nào đồng biến, nghich biến.
a) y = 1 - 5x;
b) y = -0,5x;
c)
d) y = 2x2 + 3.
Bài 2: Cho hàm số bậc nhất y = (m - 2)x + 3. Tìm các giá trị của m để hàm số:
a) Đồng biến;
b) Nghịch biến.
Bài 3: Một hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của hình đó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x.
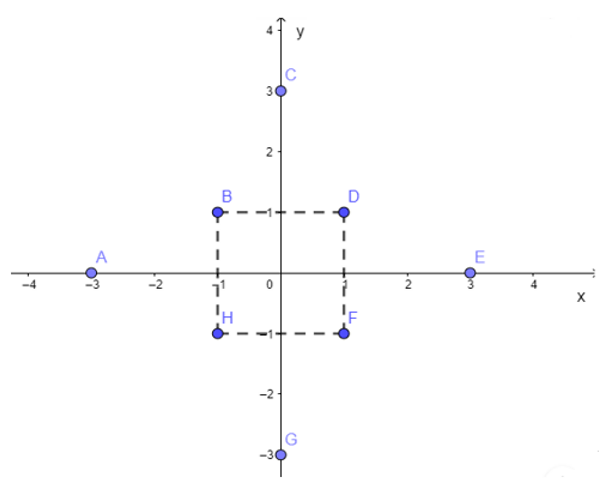
Bài 4: Hãy biểu biễn các điểm sau trên mặt phẳng tọa độ:
A(-3; 0), B(-1; 1), C(0; 3), D(1; 1), E(3; 0), E(3; 0), F(1; -1), G(0; -3), H(-1; -1).
Bài 5: Cho hàm số bậc nhất y = ax + 3. Tìm hệ số a, biết rằng khi x = 1 thì y = 2,5.
Bài 6: Với những giá trị nào của m thì mỗi hàm số sau là hàm số bậc nhất?
Bài 7: Cho hai hàm số
a) Tìm tập xác định của hàm số đã cho
b) Tính f(2); f(1/2), g(0), g(1), g(1/2)
Bài 8: Cho hàm số y = -mx + m - 3. Biết f(-2) = 6. Tính f(-3)
Bài 9: Xác định tính đồng biến, nghịch biến của các hàm số sau:
a) y = f(x) = (1 - √2)x + 1, với x ∈ R
b) 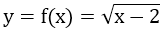
c) y = f(x) = x2 + 2,với x < 0
Bài 10: Cho hàm số y = (2m + 1)x - m + 3
a) Tìm m biết đồ thị đi qua điểm A(-2; 3)
b) Tìm điểm cố định mà đồ thị hàm số luôn đi qua với mọi giá trị của m
Bài 11: Xác định đường thẳng đi qua hai điểm A(-2; 0) và B(0; 3)
Bài 12: Với giá trị nào của m thì đồ thị các hàm số y = 2x + 4 - m và y = 3x + m - 2 cắt nhau tại một điểm trên trục tung
Bài 13: Cho hàm số y = (m - 2)x + m + 3 với m ≠ 2
a) Xác định giá trị của m để hàm số đồng biến, nghịch biến
b) Tìm m để đồ thị hàm số cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.
Bài 14: Cho hai đường thẳng
(d1 ): y = 12x + 5 - m; (d2 ): y = 3x + 3 + m
Xác định m để giao điểm của (d1 ) và (d2 ) thỏa mãn
a) Nằm trên trục tung
b) Nằm bên trái trục tung
c) Nằm trong góc phần tư thứ hai.
Bài 15: Cho đường thẳng (d):y = (m - 3)x + 3m + 2. Tìm giá trị nguyên của m để (d) cắt trục hoành tại điểm có hoành độ nguyên.
Đáp án và hướng dẫn giải
Bài 1
a) y = 1 - 5x là một hàm số bậc nhất với a = -5, b = 1. Đó là một hàm số nghịch biến vì -5 < 0.
b) y = -0,5x là một hàm bậc nhất với a ≈ -0,5, b = 0. Đó là một hàm số nghịch biến vì -0,5 < 0.
c) là một hàm số bậc nhất với
,
. Đó là một hàm số đồng biến vì
.
d) y = 2x2 + 3 không phải là một hàm số bậc nhất vì nó không có dạng y = ax + b, với a ≠ 0.
Bài 2
a) Hàm số: y=(m−2)x+3 đồng biến trên R:
⇔m−2>0⇔m>2
b) Hàm số: y=(m−2)x+3 nghịch biến trên R:
⇔m−2<0⇔m<2
Bài 3
Khi bớt mỗi kích thước x (cm) thì được một hình chữ nhật có các kích thước là 20 - x (cm) và 30 - x (cm).
Khi đó chu vi của hình chữ nhật là y=2(20−x+30−x) hay y=100−4x
Bài 4
Biểu diễn các điểm trên mặt phẳng tọa độ:
Bài 5
Theo đề bài ta có:
Hàm số: y=ax+3 đi qua điểm A(1;2,5)
Và hàm số đó là
Bài 6
Muốn cho một hàm số là hàm số bậc nhất thì nó phải có dạng y = ax + b, với a ≠ 0. Do đó:
a) Điều kiện để hàm số là hàm bậc nhất khi:
hay 5 - m > 0. Suy ra m < 5.
b) Điều kiện để hàm số là hàm bậc nhất khi:
hay m + 1 ≠ 0, m - 1 ≠ 0. Suy ra m ≠ ± 1.
Bài 7:
a) Hàm số 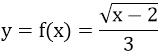
Hàm số 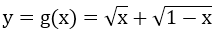
b) f(2) = 0;
f(1/2) không xác định (do 1/2 không thỏa mãn ĐKXĐ)
g(0) = 1; g(1) = 1; g(1/2) = √2
Bài 8:
y = -mx + m - 3.
Ta có: f(-2) = -m.(-2) + m - 3 = 6 ⇔ 3m - 3 = 6 ⇔ m = 3
Khi đó y = f(x) = -3x
⇒ f(-3) = -3.(-3) = 9
Bài 9:
a) 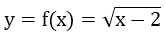
Hàm số trên là hàm bậc nhất có hệ số a=1-√2 < 0
⇒ Hàm số nghịch biến trên R
b) y = f(x) = ⇒ (x -2 ) với x ≥ 2
Lấy x1, x2 tùy ý thuộc đoạn [2; +∞) sao cho x1 > x2
Khi đó:
⇒ Hàm số đồng biến trên [2; +∞)
c) y = f(x) = x2 + 2, với x < 0
Lấy x1, x2 tùy ý thuộc đoạn (-∞;0) sao cho x1 > x2
⇒ x12 < x22 ⇒ x12 + 2 < x22 + 2 ⇒ f(x1 ) < f(x2 )
⇒ Hàm số nghịch biến trên (-∞;0)
Bài 10: y = (2m + 1)x - m + 3
a) Đồ thị đi qua điểm A(-2; 3)
⇒ 3 = (2m + 1).(-2) - m + 3
⇔ 5m = -2 ⇔ m = (-2)/5
b) Gỉa sử điểm cố định mà đồ thị hàm số đi qua với mọi m là (x0; y0 )
Khi đó: y0 = (2m + 1) x0 - m + 3 đúng với mọi m
⇔ m(2x0 - 1) + 3 + x0 - y0 = 0 đúng với mọi m
Vậy điểm cố định là (1/2; 7/2)
Bài 11:
Gỉa sử đường thẳng đi qua hai điểm A và B là y = ax + b
A(-2; 0) ∈ AB ⇒ 0 = -2a + b ⇒ b = 2a
A(0; 3) ∈ AB ⇒ 3 = a.0 + b ⇒ b = 3
⇒ a = b/2 = 3/2
Vậy phương trình đường thẳng AB là y = (3/2)x + 3
Bài 12:
Hoành độ giao điểm của 2 đường thẳng trên là nghiệm của phương trình
2x + 4 - m = 3x + m - 2 ⇔ x = 2m - 6
Hai đường thẳng trên cắt nhau tại một điểm trên trục tung nên hoành độ giao điểm bằng 0
⇒ 2m - 6 = 0 ⇔ m = 3
Vậy với m = 3 thì hai đường thẳng trên cắt nhau tại điểm nằm trên trục tung.
Bài 13:
Cho hàm số y = (m - 2)x + m + 3 với m ≠ 2
a) Hàm số đồng biến ⇔ m - 2 > 0 ⇔ m > 2
Hàm số nghịch biến ⇔ m - 2 < 0 ⇔ m < 2
b) Cho x = 0 ⇒ y = m + 3, đồ thị cắt trục tung tại điểm A(0, m + 3)
Cho y = 0 ⇒ (m - 2)x + m + 3 = 0 ⇒
Đồ thị cắt trục hoành tại điểm
⇔ (m + 3)2 = 2|m - 2|
TH1: m < 2, khi đó phương trình tương đương với:
(m + 3)2 = 4 - 2m
⇔ m2 + 8m + 5 = 0
⇔ (m + 4)2 = 11
⇔ m = -4 ± ⇒ 11
TH2: m > 2 phương trình tương đương với
(m + 3)2 = 2m - 4
⇔ m2 + 4m + 13 = 0
⇔ (m + 2)2 + 9 = 0
⇒ không tồn tại m
Vậy với m = -4 + ⇒ 11 và m = -4 - ⇒ 11 thì đồ thị hàm số cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.
Bài 14:
(d1 ): y = 12x + 5 - m; (d2 ): y = 3x + 3 + m
Hoành độ giao điểm của (d1 ) và (d2 ) là nghiệm của phương trình
12x + 5 - m = 3x + 3 + m ⇔ 9x = 2m - 2
⇒ Tọa độ giao điểm là
a) Giao điểm của (d1) và (d2) nằm trên trục tung
⇔ hoành độ giao điểm của (d1) và (d2) bằng 0.
⇔ 2m - 2 = 0 ⇔ m = 1
b) Giao điểm của (d1 ) và (d2 ) nằm bên trái trục tung
⇔ hoành độ giao điểm của (d1 ) và (d2 ) nhận giá trị âm
⇔2m - 2 < 0 ⇔ m < 1
c) Giao điểm của (d1) và (d2) nằm trong góc phần tư thứ hai.
⇔ hoành độ giao điểm nhận giá trị âm và tung độ giao điểm nhận giá trị dương.
Bài 15:
(d): y = (m - 3)x + 3m + 2.
ĐK để (d) cắt Ox là m ≠ 3
Cho y = 0 ⇒ (m - 3)x + 3m + 2 = 0
⇒ (d)cắt trục hoành tại điểm có hoành độ
x ∈ Z ⇔ m - 3 ∈ Ư(11) ⇔ m ∈ {4; 14; 2; -8}
Vậy với m ∈ {4;14;2; -8} thì (d) cắt trục hoành tại điểm có hoành độ nguyên.
Xem thêm các dạng bài tập hay, có đáp án:
30 Bài tập về Cách tìm nguyên hàm của hàm số mũ, hàm số logarit (2024) cực hay, có đáp án
60 Bài tập về Hàm số mũ, Hàm số logarit (2024) có đáp án - Toán 12
90 Bài tập hàm số. hàm số bậc hai và tam thức bậc hai (có đáp án năm 2024) - Toán 10
Cách nhận biết đồ thị hàm số mũ, hàm số logarit (2024) mới nhất