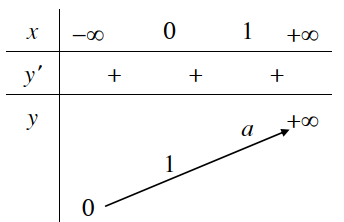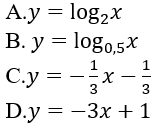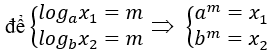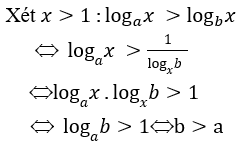Hàm số mũ, Hàm số logarit
Lý thuyết
1. Hàm số mũ
a. Định nghĩa.
Cho số thực dương a khác 1.
Hàm số y = ax được gọi là hàm số mũ cơ số a.
Ví dụ 1. Các hàm số y = 2x; là các hàm số mũ.
b. Đạo hàm của hàm số mũ
Ta thừa nhận công thức:
– Định lí 1: Hàm số y = ex có đạo hàm tại mọi x và (ex)’ = ex.
– Chú ý: Công thức đạo hàm của hàm hợp đối với hàm số eu ( với u = u(x))
là (eu)’ = u’. eu.
– Định lí 2: Hàm số y = ax ( a > 0; a ≠ 1) có đạo hàm tại mọi x và: (ax)’ = ax. ln a
– Chú ý: Đối với hàm hợp y = au(x) ta có: (au)’ = au. lnu . u’
Ví dụ 2. Hàm số có đạo hàm là:
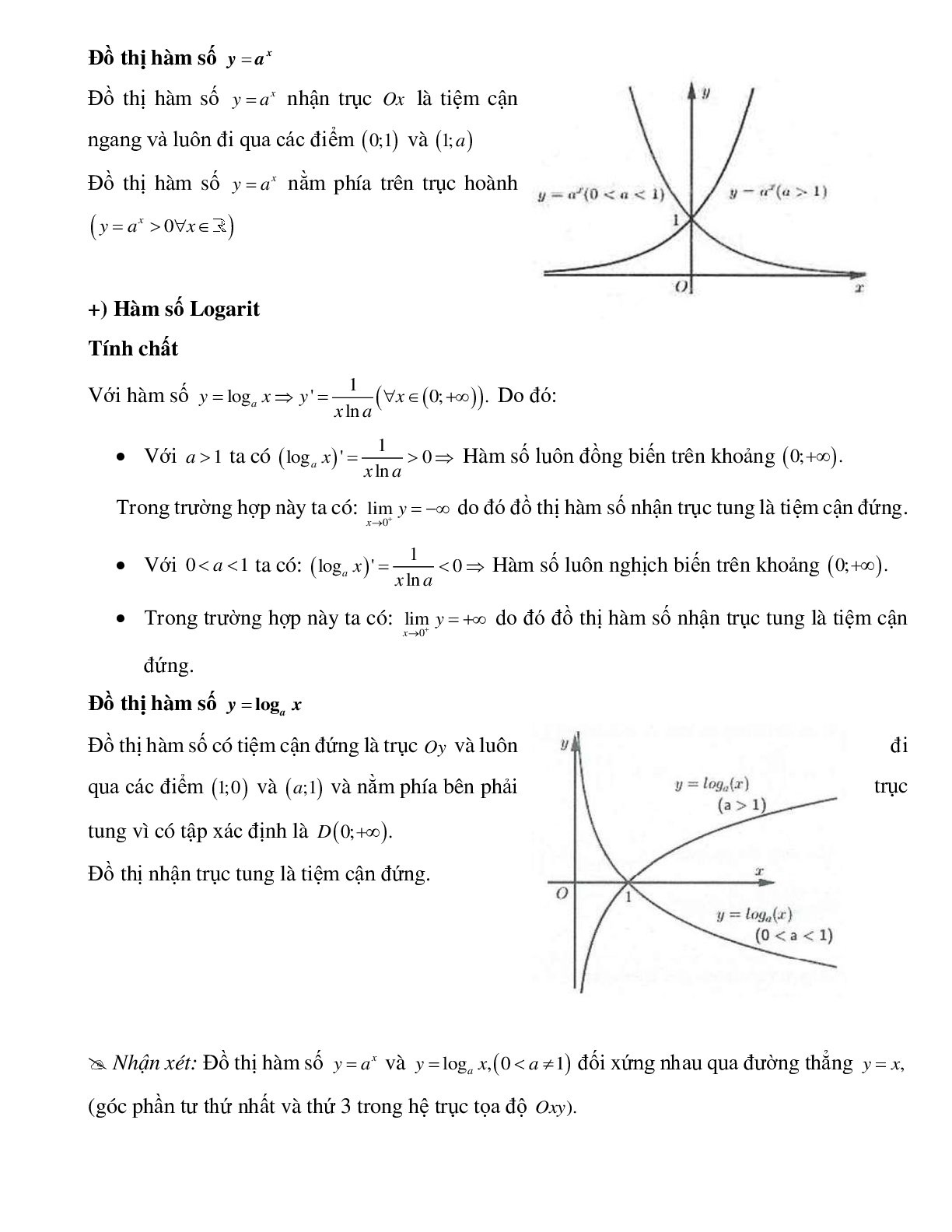
c. Khảo sát hàm số mũ y = ax ( a > 0 và a ≠ 1).
|
y = ax ; a > 1 |
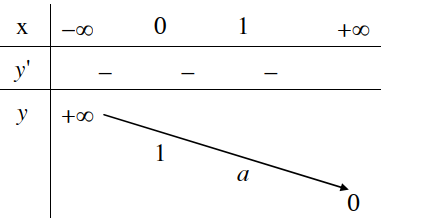
y = ax ; 0 < a < 1 |
|
1. Tập xác định: R 2. Sự biến thiên y’ = ax.ln a > 0 với mọi x Giới hạn đặc biệt:
Tiệm cận: Trục Ox là tiệm cận ngang. 3. Bảng biến thiên:
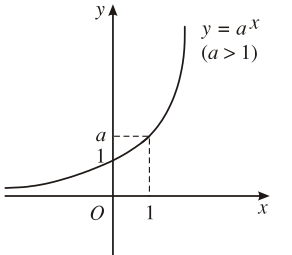
4. Đồ thị
|
1. Tập xác định: R 2. Sự biến thiên y’ = ax.ln a < 0 với mọi x Giới hạn đặc biệt:
Tiệm cận: Trục Ox là tiệm cận ngang. 3. Bảng biến thiên:
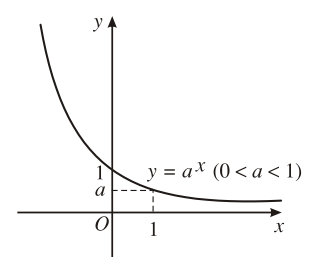
4. Đồ thị
|
d. Bảng tóm tắt các tính chất của hàm số mũ y = ax ( a > 0; a ≠ 1).
|
Tập xác định |
|
|
Đạo hàm |
y’ = ax. lna |
|
Chiều biến thiên |
a > 1: Hàm số luôn đồng biến. 0 < a < 1: Hàm số luôn nghịch biến |
|
Tiệm cận |
Trục Ox là tiệm cận ngang |
|
Đồ thị |
Đi qua các điểm (0; 1) và (1; a), nằm phía trên trục hoành (y = ax > 0 ). |
2. Hàm số logarit
a. Định nghĩa.
Cho số thực dương a khác 1.
Hàm số y = logax được gọi là hàm số logarit cơ số a.
Ví dụ 3. Các hàm số y = log5 x; ; y = ln x là các hàm số logarit với cơ số lần lượt là và e.
b. Đạo hàm của hàm số logarit
– Định lí 3. Hàm số y = loga x (a > 0; a ≠ 1) có đạo hàm tại mọi x > 0 và
– Đặc biệt:
– Chú ý:
Đối với hàm hợp y = logau(x); ta có:
– Ví dụ 4. Hàm số y = log4 (x2 + 2x – 7) có đạo hàm là:
c. Khảo sát hàm số logarit y = loga x ( a > 0; a ≠ 1).
|
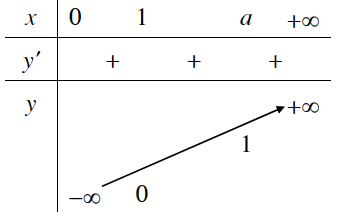
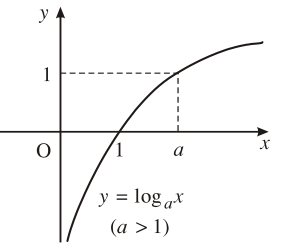
y = loga x ; a > 1 |
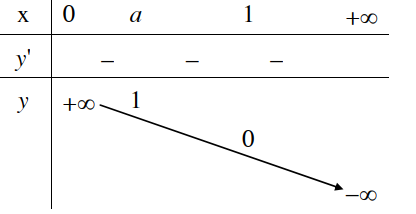
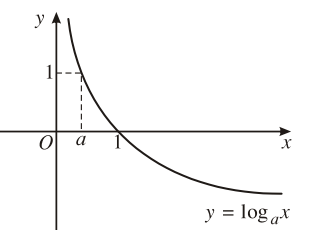
y = logax ; 0 < a < 1 |
|
1. Tập xác định: 2. Sự biến thiên
Giới hạn đặc biệt:
Tiệm cận: Trục Oy là tiệm cận đứng. 3. Bảng biến thiên
4. Đồ thị
|
1. Tập xác định: 2. Sự biến thiên
Giới hạn đặc biệt:
Tiệm cận: Trục Oy là tiệm cận đứng. 3. Bảng biến thiên
4. Đồ thị
|
d. Bảng tóm tắt các tính chất của hàm số y = logax (a > 0; a ≠ 1 ).
|
Tập xác định |
|
|
Đạo hàm |
|
|
Chiều biến thiên |
a > 1: hàm số luôn đồng biến 0 < a< 1: hàm số luôn nghịch biến |
|
Tiệm cận |
Trục Oy là tiệm cận đứng |
|
Đồ thị |
Đi qua các điểm (1; 0) và (a; 1); nằm phía bên phải trục tung |
Nhận xét:
Đồ thị của các hàm số y = ax và y = loga x ( a > 0; a ≠ 1) đối xứng với nhau qua đường thẳng y = x.
e. Bảng đạo hàm của các hàm số lũy thừa, mũ, logarit.

Bài tập vận dụng (có đáp án)
Bài 1: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đồ thị hàm số lôgarit nằm bên phải trục tung
B. Đồ thị hàm số lôgarit nằm bên trái trục tung
C. Đồ thị hàm số mũ nằm bên phải trục tung
D. Đồ thị hàm số mũ nằm bên trái trục tung
Lời giải:
Đáp án : A
Giải thích :
Hàm số lôgarit chỉ xác định khi nên đồ thị hàm số nằm bên phải trục tung.
Bài 2: Chọn phát biểu sai trong các phát biểu sau?
A. Đồ thị hàm số logarit nằm bên trên trục hoành
B. Đồ thị hàm số mũ không nằm bên dưới trục hoành
C. Đồ thị hàm số lôgarit nằm bên phải trục tung
D. Đồ thị hàm số mũ với số mũ âm luôn có hai tiệm cận.
Lời giải:
Đáp án : A
Giải thích :
Đồ thị hàm số lôgarit nằm bên phải trục tung và cả dưới, cả trên trục hoành
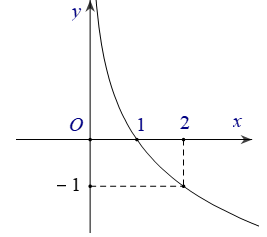
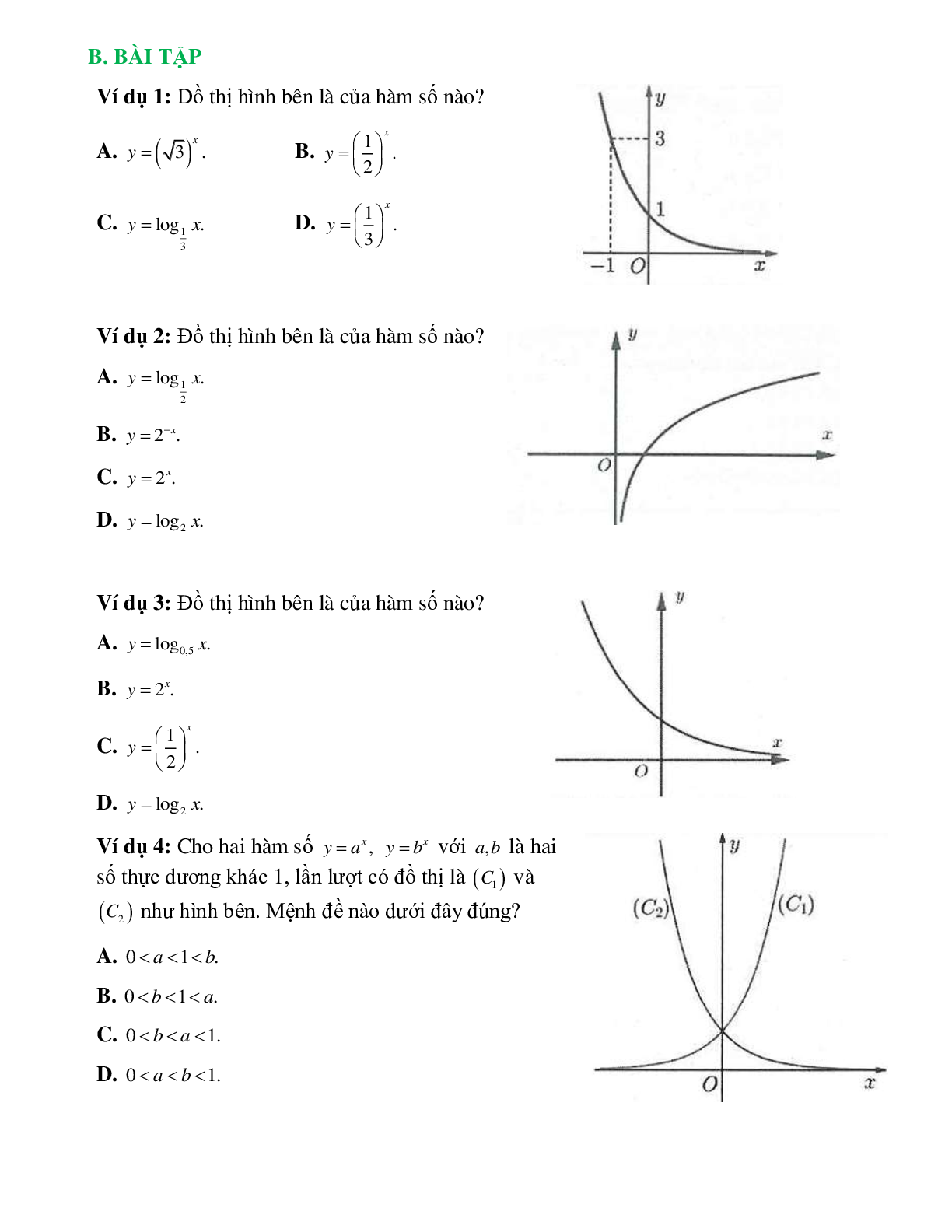
Bài 3: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Lời giải:
Đáp án : B
Giải thích :
Nhận thấy đây là đồ thị hàm số y=logax. Điểm A(2;-1) thuộc đồ thị hàm số nên
-1=loga2 ⇒ a-1=2 ⇒ 1/a=2 ⇒ a=0,5. Hàm số y=log0,5x
Bài 4: Tìm a để hàm số y=logax (0 < a ≠ 1) có đồ thị là hình bên dưới:
A. a=1/√2
B. a=-1/√2
C. a=1/2
D. a=√2
Lời giải:
Đáp án : D
Giải thích :
Đồ thị hàm số đi qua A(2;2) ⇒ 2=loga2 ⇒ a2=2 ⇒ a=√2 .
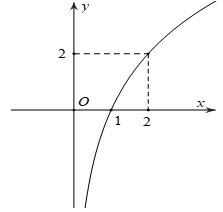
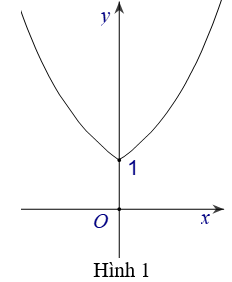
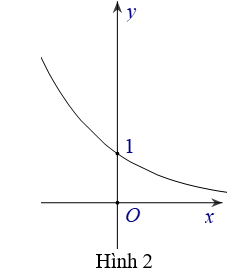
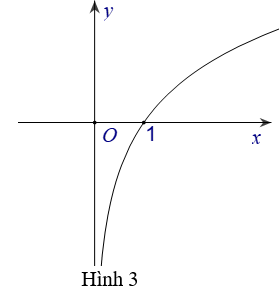
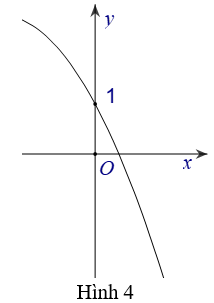
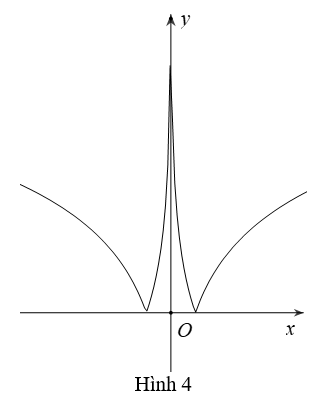
Bài 5: Biết hàm số y=2x có đồ thị là hình bên.
Khi đó, hàm số y=2|x| có đồ thị là hình nào trong bốn hình được liệt kê ở bốn A, B, C, D dưới đây ?
A. Hình 3
B. Hình 2
C. Hình 1
D. Hình 4
Lời giải:
Đáp án : A
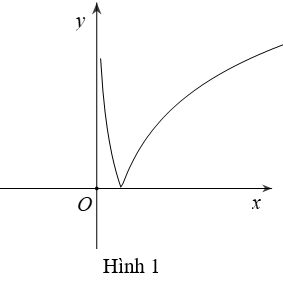
Bài 6: Cho hàm số y=log2(2x). Khi đó, hàm số y=|log2(2x)|. có đồ thị là hình nào trong bốn hình được liệt kê ở bốn phương án A, B, C, D dưới đây:
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Lời giải:
Đáp án : A
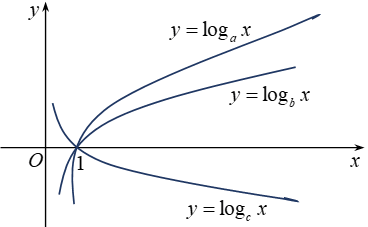
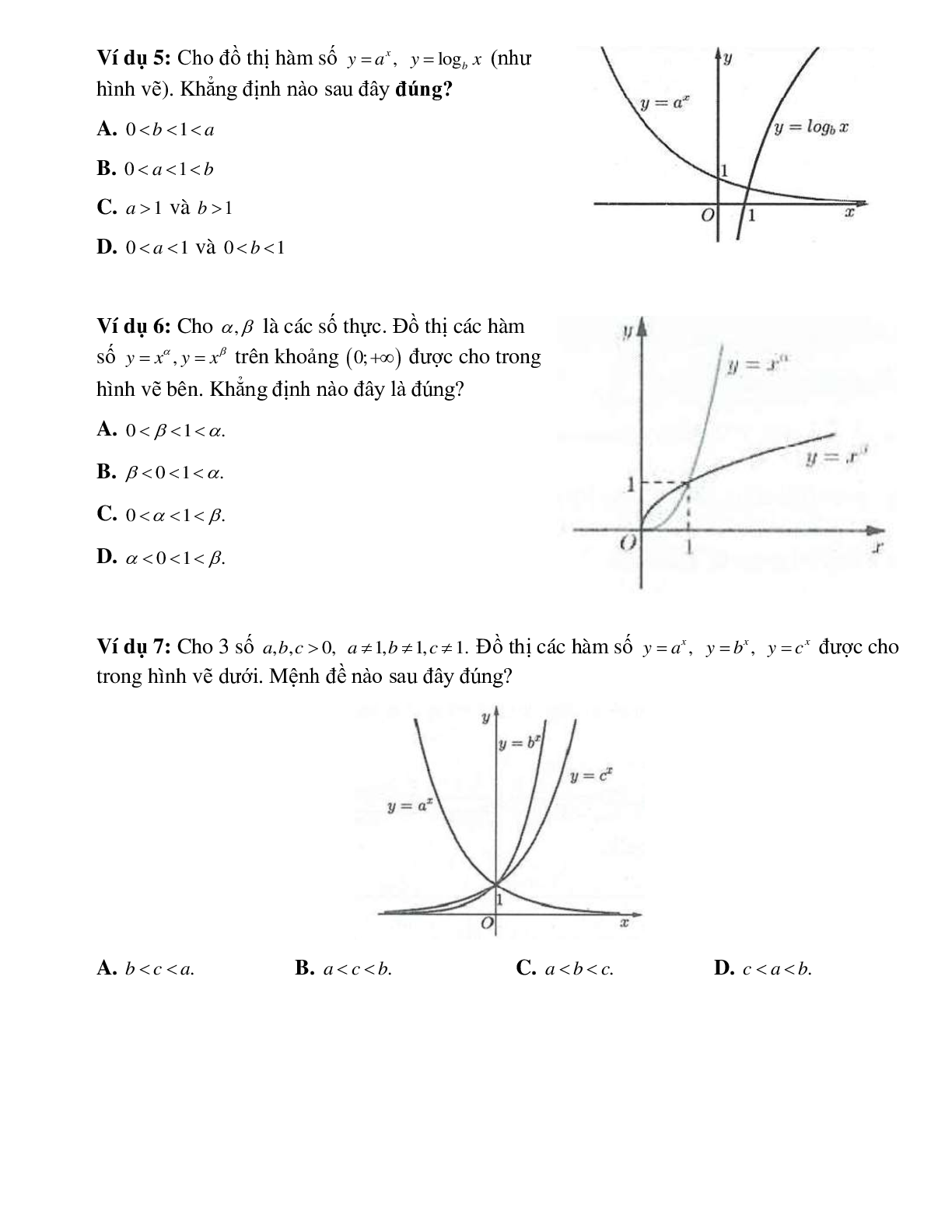
Bài 7: Hình bên là đồ thị của ba hàm số y=logax, y=logbx, y=logcx (0 < a, b, c ≠ 1) được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
A. b > c > a
B. a > b > c
C. b > a > c
D. a > c > b
Lời giải:
Đáp án : C
Giải thích :
Do y=logax và y=logbx là hai hàm dồng biến nên a,b > 1
Do y=logcx nghịch biến nên c < 1. Vậy c bé nhất.
Mặt khác: Lấy y=m, khi đó tồn tại x1,x2 > 0
Dễ thấy x1 < x2 ⇒ am < bm ⇒ a < b
Vậy b > a > c.
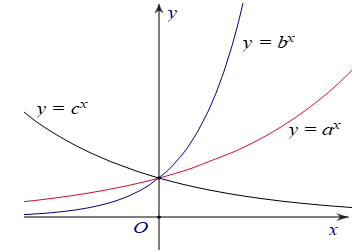
Bài 8: Hình bên là đồ thị của ba hàm số y=ax, y=bx, y=cx được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
A. c > b > a
B. a > b > c
C. a > c > b
D. b > a > c
Lời giải:
Đáp án : D
Giải thích :
Do y=ax và y=bx là hai hàm đồng biến nên a, b > 1
Do y=cx nghịch biến nên c < 1. Vậy x bé nhất.
Mặt khác: Lấy x=m, khi đó tồn tại y1, y2 > 0
Dễ thấy
Vậy b > a > c
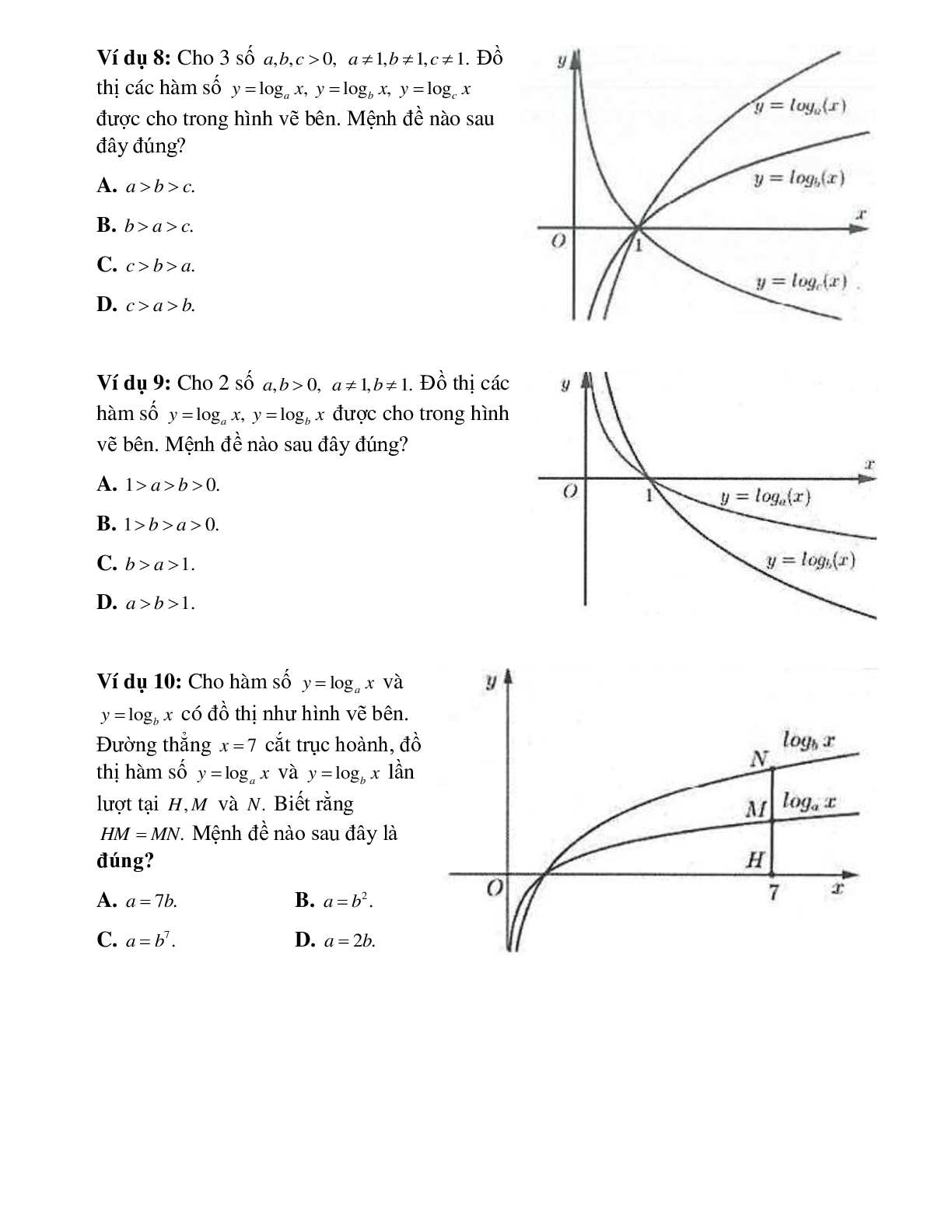
Bài 9: Hàm số nào có đồ thị như hình vẽ bên?
A. y=(1/3)x
B. y=(1/√2)x
C. y=3x
D. y=(√2)x
Lời giải:
Đáp án : A
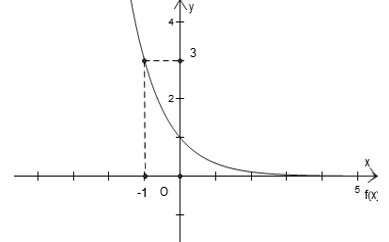
Bài 10: Từ các đồ thị số y=logax, y=logbx, y=logcx (0 < a, b, c ≠ 1) đã cho ở hình vẽ. Khẳng định nào sau đây đúng?
A. 0 < a < b < 1 < c
B. 0 < c < 1 < a < b
C. 0 < c < a < 1 < b
D. 0 < c < 1 < b < a
Lời giải:
Đáp án : A
Giải thích :
Ta thấy hàm số nghịch biến và đồ thị đi qua (0;1);(-1;3).
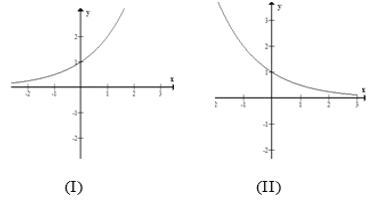
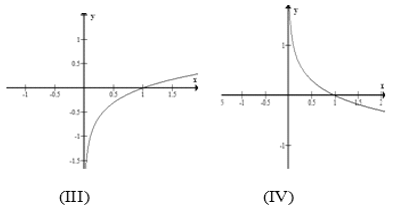
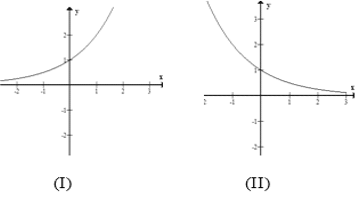
Bài 11: Trong các hình sau hình nào là dạng đồ thị của hàm số
A. (I)
B. (II)
C. (IV)
D. (III)
Lời giải:
Đáp án : B
Giải thích :
Hàm số y=logax và y=logbx đồng biến trên (0;+∞)⇒ a, b > 1
Hàm số y=logcx nghịch biến trên(0;+∞)⇒ 0 < c < 1
Suy ra 0 < c < 1 < a < b
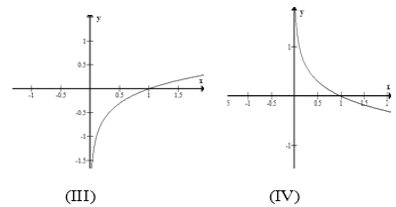
Bài 12: Trong các hình sau hình nào là dạng đồ thị của hàm số
A. (I)
B. (II)
C. (III)
D. (IV)
Lời giải:
Đáp án : B
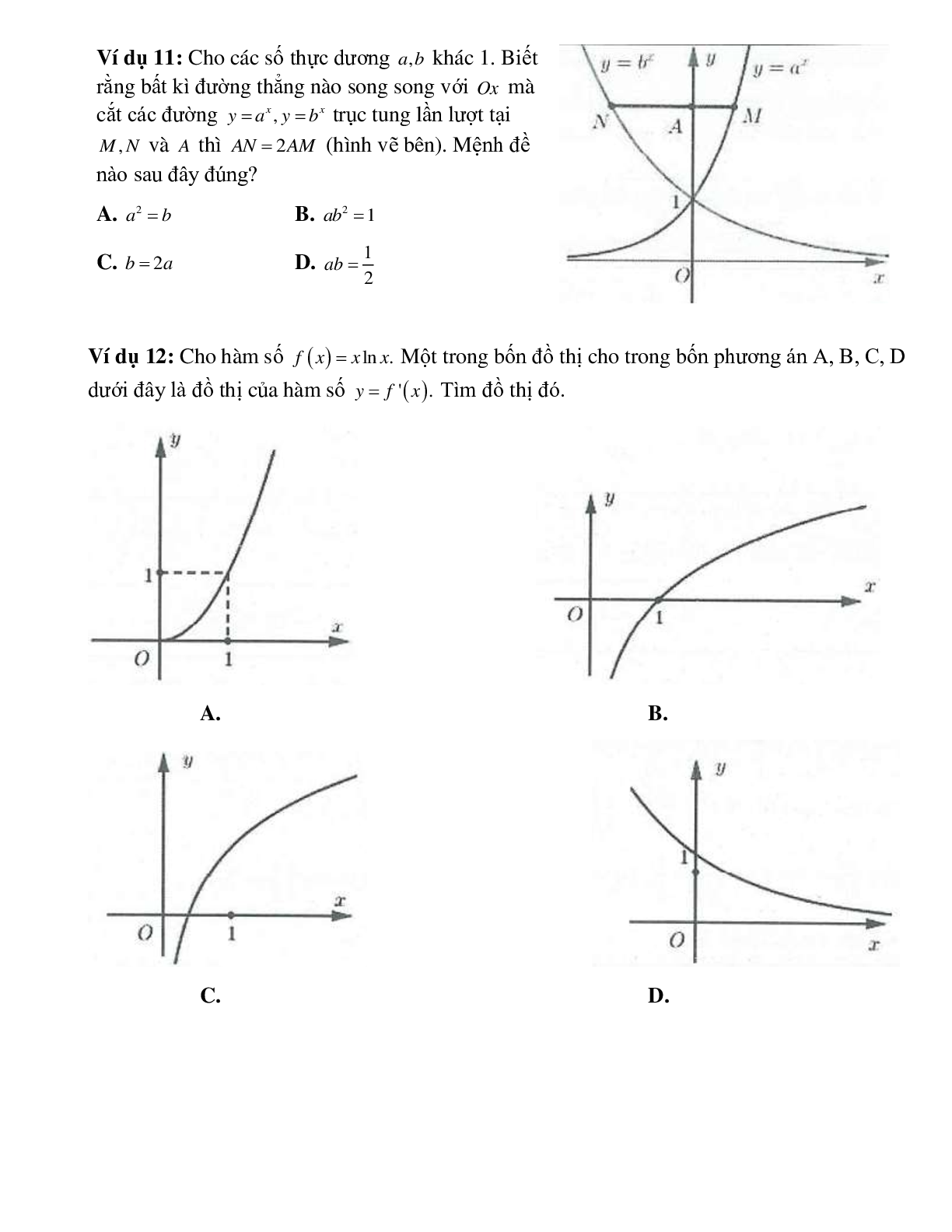
Bài 13: Cho bốn hàm số y=(√3)x (1),y=(1/√3)x (2),y=4x (3),y=(1/4)x (4) và bốn đường cong(C1),(C2),(C2),(C4) như hình vẽ bên. Đồ thị các hàm số (1), (2), (3), (4) lần lượt là:
A. (C2), (C3), (C4), (C1)
B. (C1), (C2), (C3), (C4)
C. (C4), (C1), (C3), (C2)
D. (C1), (C2), (C4), (C3)
Lời giải:
Đáp án : C
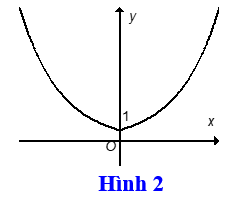
Bài 14: Cho hàm số y=(√2)x có đồ thị Hình 1 . Đồ thị Hình 2 là của hàm số nào dưới đây?
A. y=|(√2)x |
B. y=-(√2)x
C. y=(√2)|x|
D. y= -|(√2)x |
Lời giải:
Đáp án : C
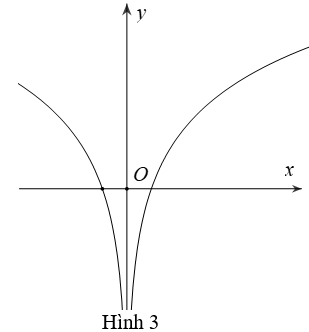
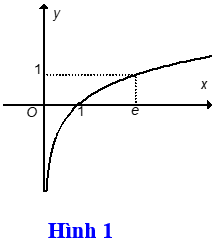
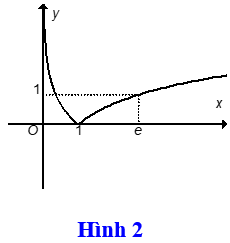
Bài 15: Cho hàm số y=lnx có đồ thị như Hình 1, Đồ thị Hình 2 là của hàm số nào dưới đây?
A. y=ln|x|
B. y=|lnx |
C. y=|ln(x+1) |
D. y=ln|x+1|
Lời giải:
Đáp án : B
Xem thêm các dạng bài tập Toán chi tiết và hay khác:
60 Bài tập về Hàm số lũy thừa (có đáp án năm 2023)
60 Bài tập về Lôgarit (có đáp án năm 2023)
60 Bài tập về Phương trình mũ và phương trình logarit (có đáp án năm 2023)
60 Bài tập về Bất phương trình mũ và bất phương trình logarit (có đáp án năm 2023)