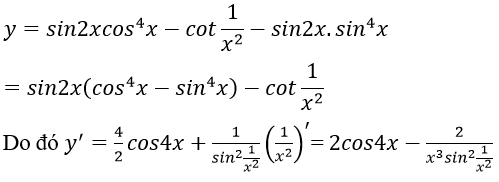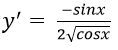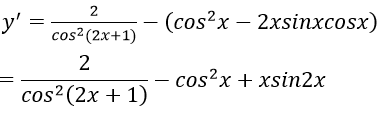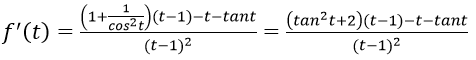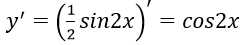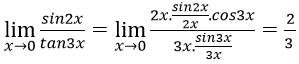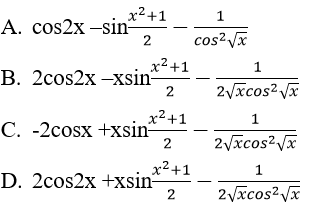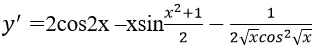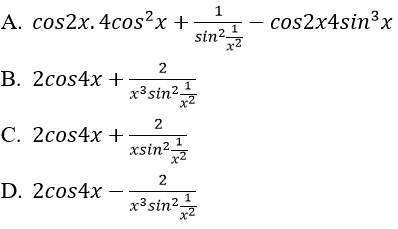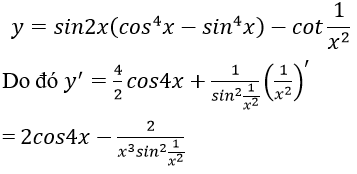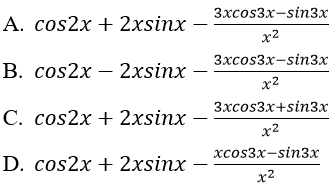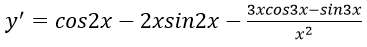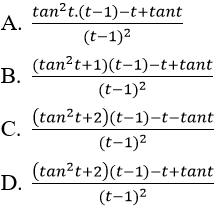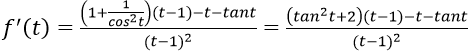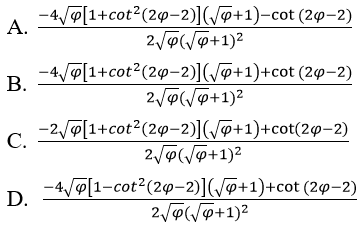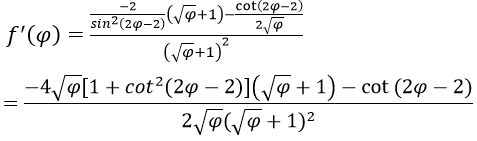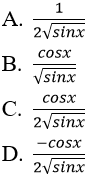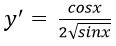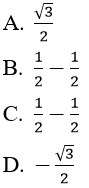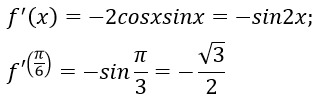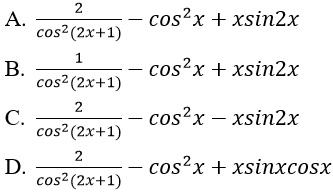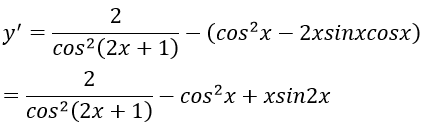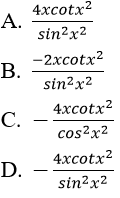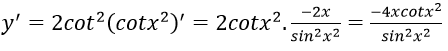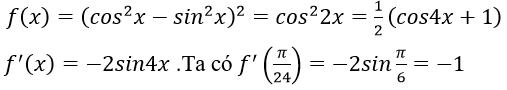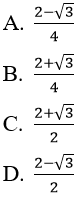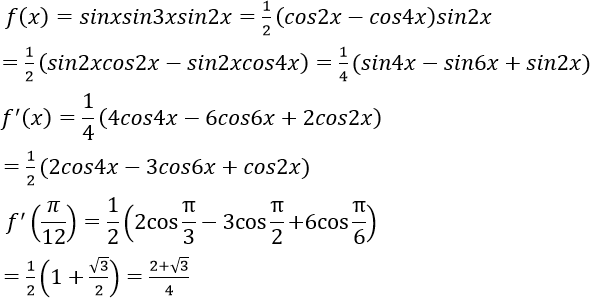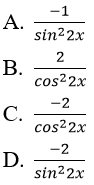Đạo hàm của hàm số lượng giác
LÝ THUYẾT
1. Giới hạn
Định lý 1.
Ví dụ 1. Tính
Lời giải
Đặt x – 1 = t.
Khi x tiến đến 1 thì t tiến đến 0.
2. Đạo hàm của hàm số y = sinx
Định lý 2.
Hàm số y = sinx có đạo hàm tại mọi và (sinx)’ = cosx.
Chú ý:
Nếu y = sinu và u = u(x) thì: (sinu)’ = u’.cosu
Ví dụ 2. Tính đạo hàm của hàm số
Lời giải
3. Đạo hàm của hàm số y = cosx
Định lý 3.
Hàm số y = cosx có đạo hàm tại mọi và (cosx)’ = - sinx.
Chú ý:
Nếu y = cosu và u = u(x) thì: (cosu)’ = - u’.sinu
Ví dụ 3. Tính đạo hàm của hàm số tại .
Lời giải
Đặt
Thay vào y’ ta được:
Vậy giá trị của đạo hàm của hàm số tại là
4. Đạo hàm của hàm số y = tanx
Định lý 4.
Hàm số y = tanx có đạo hàm tại mọi và (tanx)’ = .
Chú ý:
Nếu y = u và u = u(x) thì: (tanu)’ =
Ví dụ 4. Tính đạo hàm
Lời giải
Đặt u = 2 + tanx
5. Đạo hàm của hàm số y = cotx
Định lý 5.
Hàm số y = cotx có đạo hàm tại mọi và (cotx)’ = .
Chú ý:
Nếu y = u và u = u(x) thì: (cotu)’ =
Ví dụ 5. Tính đạo hàm của hàm y = cot x2.
Lời giải
y’ = (cot x2)’ = (x2)’.=.
6. Bảng quy tắc tính đạo hàm tổng hợp:

BÀI TẬP VẬN DỤNG (CÓ ĐÁP ÁN)
Bài 1. Tính các đạo hàm sau:
a)
b)
c)
d)
Lời giải
a)
b)
c)
d)
Bài 2. Chứng minh rằng các hàm số sau đây có đạo hàm không phụ thuộc x.
a)
b)
Lời giải
a)
b)
Bài 3. Tìm f’(2) biết f(x) = x2.sin(x – 2).
Lời giải
Ta có : f’(x) = 2x.sin(x – 2) + x2cos(x – 2)
Khi đó: f’(2) = 2.2.sin(2 – 2) + 22.cos(2 – 2)
= 4.0 + 4.1
= 0 + 4
= 4.
Vậy f’(2) = 4.
Bài 4: Đạo hàm của hàm số:
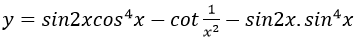
Lời giải
Bài 5: Tính đạo hàm của hàm số y = cos2x + cos4x + sin5x
Lời giải
Ta có: y' = -2sin2x - 4sin4x + 5cos5x
Bài 6: Đạo hàm của hàm số y = √cosx bằng biểu thức nào?
Lời giải
Bài 7: Đạo hàm của hàm số y = tan(2x+1) - xcos2x bằng biểu thức nào?
Lời giải
Bài 8: Đạo hàm của hàm số 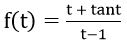
Lời giải
Bài 9: Đạo hàm của hàm số y = 6(sin4x + cos4x) - 4(sin6x + cos6x) bằng biểu thức nào?
Lời giải
y' = 6(sin2x + cos2x)2 - 12sin2xcos2x - 4(sin2x + cos2x)2 + 12sin2xcos2x(sin2x + cos2x) = 2
Bài 10: Tính đạo hàm của hàm số: y = sinx.cosx
Lời giải
BÀI TẬP TỰ LUYỆN (CÓ ĐÁP ÁN)
Bài 1: 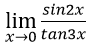
A. 1 B. 0 C. 2/3 D. 3/2
Lời giải:
Đáp án: C
Đáp án C
Bài 2: Đạo hàm của hàm số:
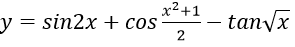
Lời giải:
Đáp án: B
Đáp án B
Bài 3: Đạo hàm của hàm số:
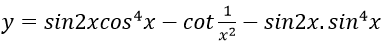
Lời giải:
Đáp án: D
Đáp án D
Bài 4: Đạo hàm cuả hàm số:
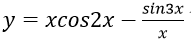
Lời giải:
Đáp án: B
Chọn đáp án B
Bài 5: Đạo hàm của hàm số:
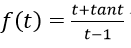
Lời giải:
Đáp án: C
Chọn đáp án C
Bài 6: Đạo hàm của hàm số:
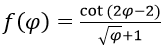
Lời giải:
Đáp án: A
Chọn đáp án A
Bài 7: Đạo hàm của hàm số y = 6(sin4x + cos4x) - 4(sin6x + cos6x) bằng biểu thức nào sau đây?
A. 24(sin3x + cos3x) - 24(sin5x + cos5x)
B. 24(sin3x - cos3x) - 24(sin5x + cos5x)
C. 2
D. 0
Lời giải:
Đáp án: D
y'= 6(sin2x + cos2x)2 - 12sin2xcos2x - 4(sin2x + cos2x)2 + 12sin2xcos2x(sin2x + cos2x) = 2
Chọn đáp án D
Bài 8: Đạo hàm của hàm số y = √sinx bằng biểu thức nào sau đây:
Lời giải:
Đáp án: C
Chọn đáp án C
Bài 9: Cho hàm số f(x) = cos2x. Giá trị của f'(π/6) bằng:
Lời giải:
Đáp án: D
Chọn đáp án D
Bài 10: Đạo hàm của hàm số y = tan(2x+1) - xcos2x bằng biểu thức nào sau đây:
Lời giải:
Đáp án: A
Chọn đáp án A
Bài 11: Đạo hàm của hàm số y = cot2x2 bằng biểu thức nào sau đây:
Lời giải:
Đáp án: D
Chọn đáp án D
Bài 12: Cho hàm số f(x) = sin4x + cos4x - 2sin2x cos2x. Giá trị của f'(π/24) bằng:
A. -1
B. 1
C. 1/2
D. (-1)/2
Lời giải:
Đáp án: A
Chọn đáp án A
Bài 13: Cho hàm số f(x) = sinx.sin2x.sin3x. Giá trị của f'(π/12)bằng:
Lời giải:
Đáp án: B
Chọn đáp án B
Bài 14: Đạo hàm của hàm số f(x) = cot2x bằng biểu thức nào sau đây?
Lời giải:
Đáp án: C
Chọn đáp án C
Bài 15: Đạo hàm cấp hai của hàm số y = cos2x bằng biểu thức nào sau đây?
A. -2sin2x
B. -4cos2x
C. -4sin2x
D. 4cos2x
Lời giải:
Đáp án: C
y’ = (cos2x)’= -4sin2x
Chọn đáp án C
Xem thêm các dạng bài tập toán hay khác:
60 Bài tập về ứng dụng hình học của tích phân (có đáp án năm 2023)
60 Bài tập về Nguyên hàm ( có đáp án năm 2023 )
60 Bài tập về số phức (có đáp án năm 2023)
60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024) có đáp án