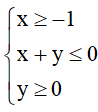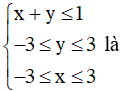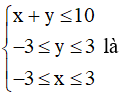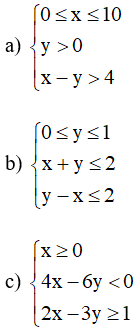30 Bài tập về miền nghiệm của bất phương trình
I. Phương pháp giải
1. Phương pháp xác định miền nghiệm của bất phương trình ax + by + c > 0
Bước 1: Vẽ đường thẳng (d): ax + by + c = 0
Bước 2: Lấy một điểm M(x0; y0) không thuộc đường thẳng d
Bước 3: Tính A = ax0 + by0 + c
-
Nếu A > 0 thì M thuộc miền nghiệm ta gạch chéo phần mặt phẳng không chứa M.
-
Nếu A < 0 thì M không thuộc miền nghiệm, nên ta sẽ gạch chéo phần mặt phửng chứa M
Chú ý:
-
Nếu có dấu bằng ta sẽ lấy cả đường thẳng (d), còn không có dấu bằng thì ta không lấy đường thẳng (d)
-
Nếu bài toán yêu cầu xác định miền nghiệm của bất phương trình ax + by + c < 0 thì ta sẽ làm bước 1;
-
bước 2 như trên nhưng trong bước 3, miền nghiệm sẽ gạch ngược lại.
2. Phương pháp xác định miền nghiệm của hệ bất phương trình
Bước 1: Xác định miền nghiệm của từng bất phương trình.
Bước 2: Phần còn lại không gạch chéo trong mặt phẳng tọa độ chính là miền nghiệm của hệ bất phương
trình đã cho.
3. Ví dụ minh họa
Ví dụ 1. Xác định miền nghiệm của các bất phương trình sau:
a) 2x−y≥0.
b) x−2y2>2x+y+13.
Lời giải:
a) Trong mặt phẳng tọa độ, vẽ đường thẳng (d): 2x−y=0, ta có (d) chia mặt phẳng thành hai nửa mặt phẳng.
Chọn một điểm bất kì không thuộc đường thẳng đó, chẳng hạn điểmM(1;0), ta thấy (1;0) là nghiệm của bất
phương trình đã cho.
Vậy miền nghiệm cần tìm là nửa mặt phẳng chứa bờ (d) và chứa điểm M(1;0) (miền không được tô màu
trên hình vẽ).
b) Ta có x−2y2>2x−y+13 ⇔3(x−2y)−2(2x−y+1)>0 ⇔−x−4y−2>0 ⇔x+4y+2<0.
Trong mặt phẳng tọa độ, vẽ đường thẳng Δ:x+4y+2=0.
Xét điểm O(0;0), ta thấy (0;0) không phải là nghiệm của bất phương trình đã cho do đó miền nghiệm cần tìm
là nửa mặt phẳng bờ Δ (không kể đường thẳng Δ) và không chứa điểm O(0;0) (miền không được tô màu
trên hình vẽ).
Ví dụ 2. Xác định miền nghiệm của các hệ bất phương trình sau:
a) {x+y−2≥0x−3y+3≤0
b) ⎧⎩⎨x+y>02x−3y+6>0x−2y+1≥0
Lời giải:
a) Vẽ các đường thẳng (d):x+y−2=0, (d′):x−3y+3=0 trên mặt phẳng tọa độ Oxy.
Xét điểm O(0;0), thấy (0;0) không phải là nghiệm của bất phương trình x+y−2≥0 và x−3y+3≤0.
Do đó miền nghiệm cần tìm là phần mặt phẳng không được tô màu trên hình vẽ kể cả hai đường
thẳng (d) và (d′).
b) Vẽ các đường thẳng (d):x+y=0, (d′):2x−3y+6=0 và (d”):x−2y+1=0 trên mặt phẳng tọa độ Oxy.
Xét điểm O(0;0), thấy (0;0) là nghiệm của bất phương trình 2x−3y+6>0 và x−2y+1≥0.
Do đó O(0;0) thuộc miền nghiệm của bất phương trình 2x−3y+6>0 và x−2y+1≥0.
Xét điểm M(1;0) ta thấy (1;0) là nghiệm của bất phương trình x+y>0 do đó điểm M(1;0) thuộc miền nghiệm
bất phương trình x+y>0.
Vậy miền nghiệm cần tìm là phần mặt phẳng không được tô màu trên hình vẽ kể cả đường thẳng (d”).
Ví dụ 3. Xác định miền nghiệm bất phương trình (x−y)(x3+y3)≥0.
Ta có (x−y)(x3+y3)≥0 ⇔(x−y)(x+y)(x2−xy+y2)≥0 ⇔(x−y)(x+y)≥0 ⇔{x−y≥0x+y≥0 (1) hoặc {x−y≤0x+y≤0 (2).
Như vậy miền nghiệm của bất phương trình đã cho là gồm hai miền nghiệm của hệ bất phương trình
(1) và (2).
Vẽ các đường thẳng (d):x+y=0, (d′):x−y=0 trên mặt phẳng tọa độ Oxy.
Xét điểm M(1;0), ta có (1;0) là nghiệm của các bất phương trình của hệ (1) do đó M(1;0) thuộc miền nghiệm
của hệ bất phương trình (1).
Xét điểm N(−1;0), ta có (−1;0) là nghiệm của các bất phương trình của hệ (2) do đó N(−1;0) thuộc miền
nghiệm của hệ bất phương trình (2).
Vậy miền nghiệm cần tìm là phần mặt phẳng không được tô màu trên hình vẽ kể cả hai đường
thẳng (d), (d′).
 II. Bài tập vận dụng
II. Bài tập vận dụng
Bài 1: Biểu diễn miền nghiệm của hệ bất phương trình:
a) {x+2y<−4 y≥x+5;
b) {4x−2y>8x≥0y≤0.
Lời giải:
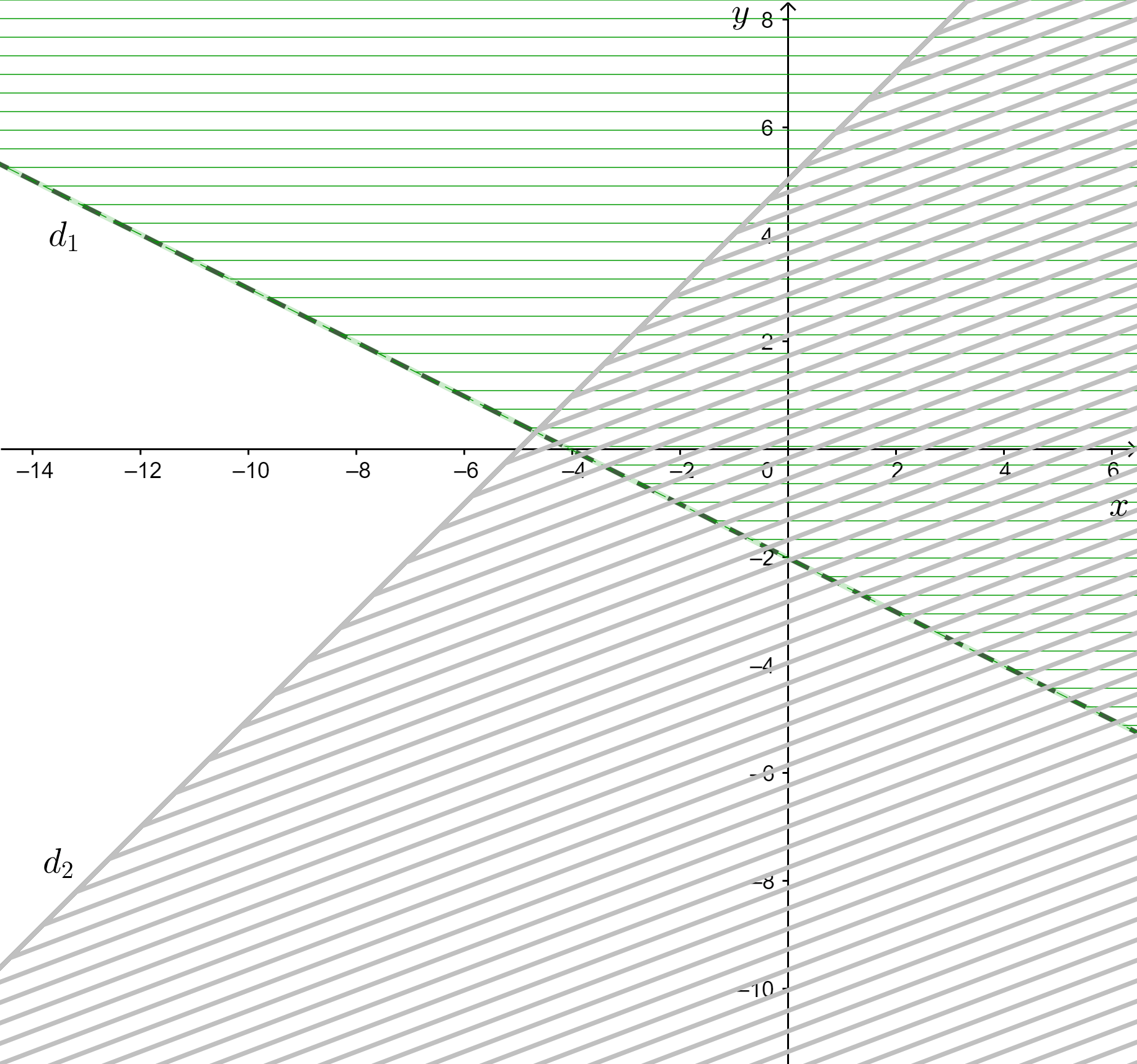
a) {x+2y<−4 y≥x+5⇔{x+2y<−4−x+y≥5
+ Trên cùng một mặt phẳng tọa độ Oxy, vẽ các đường thẳng:
d1: x + 2y = – 4;
d2: – x + y = 5.
+ Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là phần không gạch sọc trên hình bao gồm một phần đường
biên d2, không bao gồm đường biên d1.
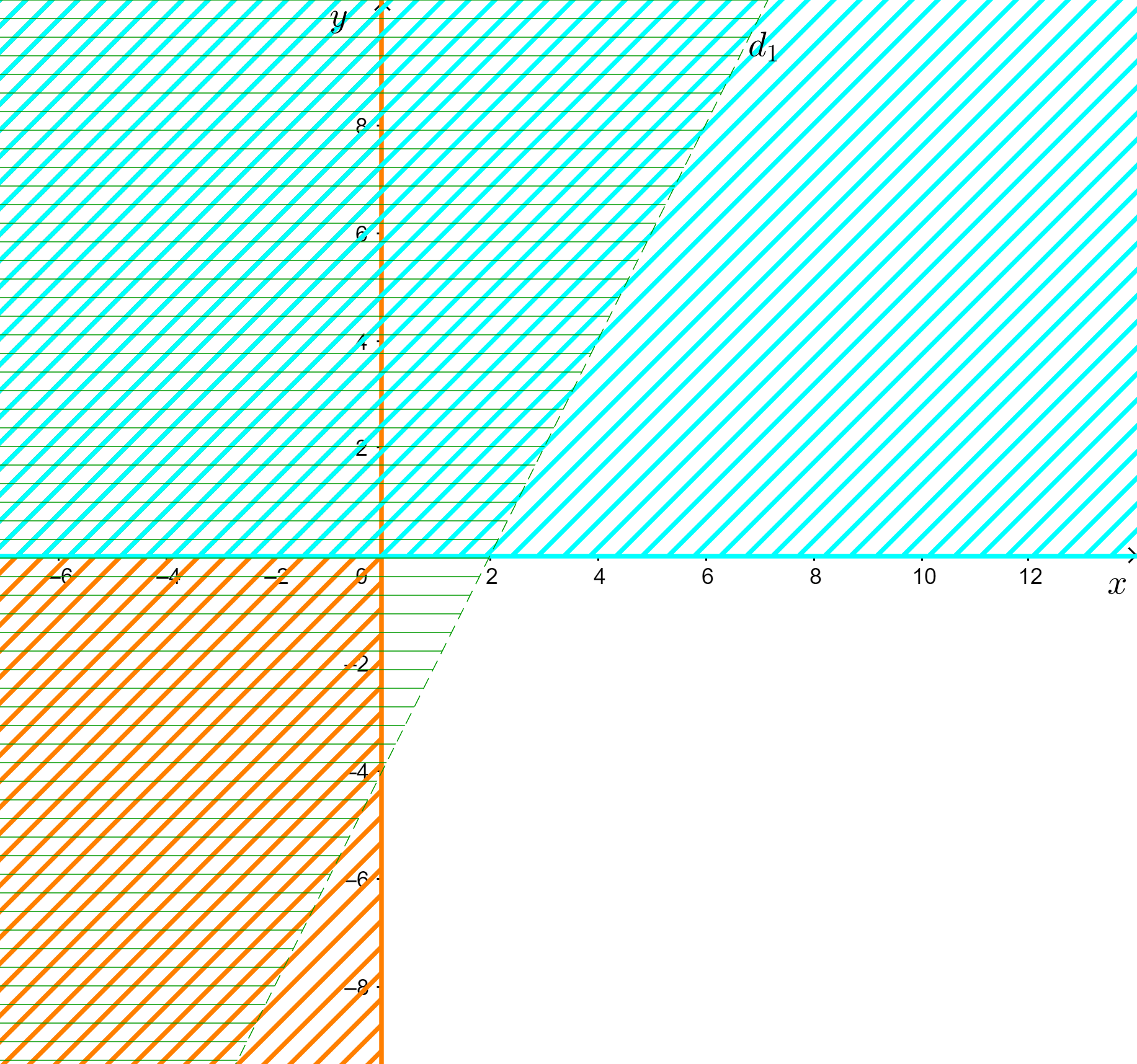
b) {4x−2y>8x≥0y≤0.
+ Trên cùng một mặt phẳng tọa độ Oxy, vẽ các đường thẳng:
d1: 4x – 2y = 8;
d2: x = 0 là trục tung;
d3: y = 0 là trục hoành.
+ Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là phần không gạch sọc trên hình bao gồm một phần trục tung,
trục hoành và không bao gồm đường thẳng d1.
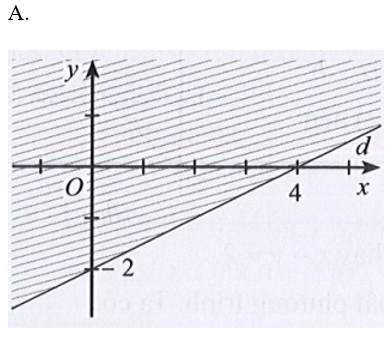
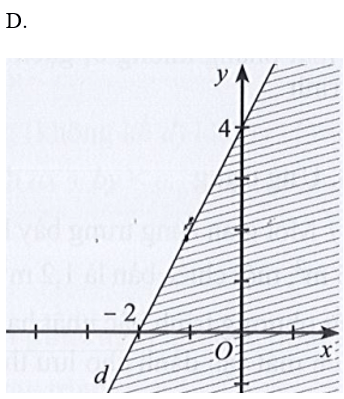
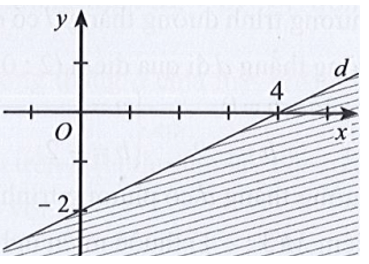
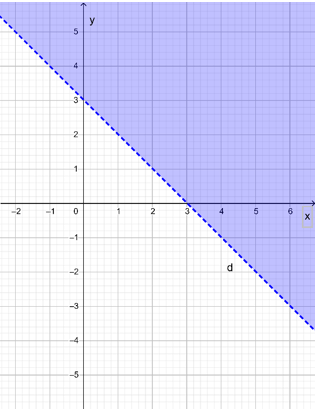
Bài 2: Miền nghiệm của bất phương trình x – 2y < 4 được xác định bởi miền nào (nửa mặt phẳng không bị gạch và không kể d) sau đây?
Lời giải:
Đáp án đúng là B
Phương trình đường thẳng d có dạng: x – 2y = 4.
Đường thẳng d cắt hai trục tọa độ Ox, Oy lần lượt tại hai điểm có tọa độ (4; 0) và (0; – 2).
Ta có: 0 – 2.0 = 0 < 4 (luôn đúng). Do đó miền nghiệm của bất phương trình chứa điểm (0; 0) và không chứa đường thẳng d.
Khi đó miền nghiệm là nửa mặt phẳng không bị gạch và không kể d được thể hiện trong hình vẽ sau:
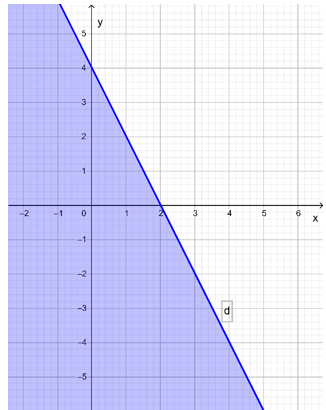
Bài 3: Miền nghiệm của bất phương trình 2x – 3y > 5 là nửa mặt phẳng (không kể đường thẳng d: 2x – 3y = 5) không chứa điểm có tọa độ nào sau đây?
A. (0; 0);
B. (3; 0);
C. (1; – 2);
D. (– 3; – 4).
Lời giải:
Đáp án đúng là B
+) Thay x = 0, y = 0 vào bất phương trình 2x – 3y > 5, ta được:
2.0 – 3.0 > 5 ⇔ 0 > 5 (vô lí)
Do đó cặp số (0; 0) không thuộc miền nghiệm của bất phương trình đã cho.
+) Thay x = 3, y = 0 vào bất phương trình 2x – 3y > 5, ta được:
2.3 – 3.0 > 5 ⇔ 6 > 5 (thỏa mãn)
Do đó cặp số (0; 0) thuộc miền nghiệm của bất phương trình đã cho.
+) Thay x = 1, y = – 2 vào bất phương trình 2x – 3y > 5, ta được:
2.1 – 3.(– 2) > 5 ⇔ 8 > 5 (thỏa mãn)
Do đó cặp số (1; – 2) thuộc miền nghiệm của bất phương trình đã cho.
+) Thay x = – 3, y = –4 vào bất phương trình 2x – 3y > 5, ta được:
2.(– 3) – 3.(– 4) > 5 ⇔ 6 > 5 (thỏa mãn)
Do đó cặp số (– 3; – 4) thuộc miền nghiệm của bất phương trình đã cho.
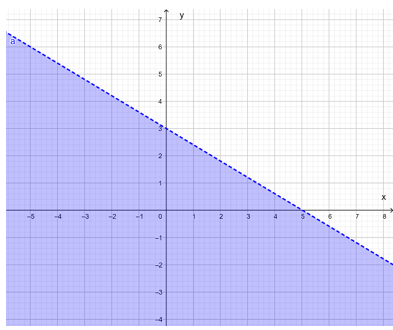
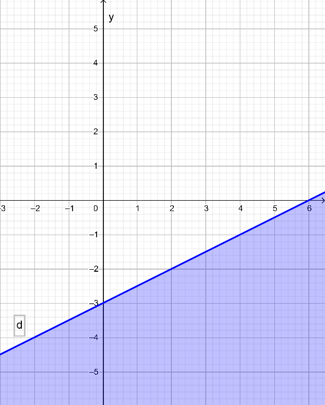
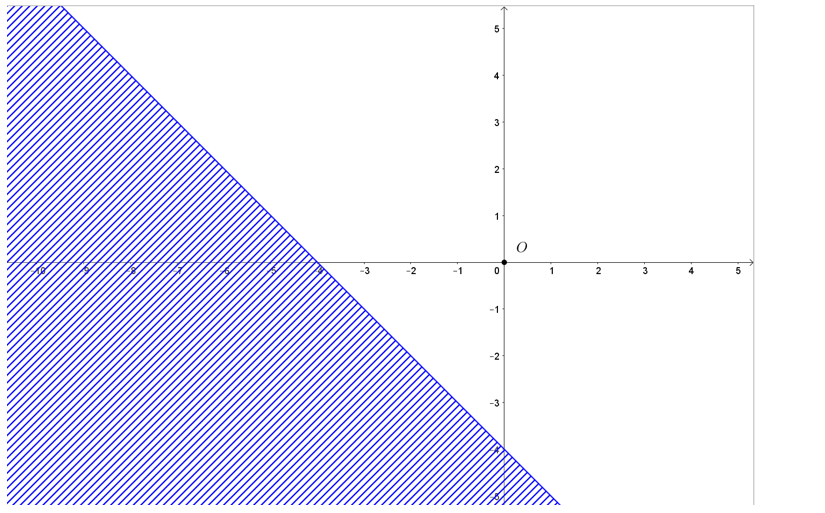
Bài 4: Biểu diễn miền nghiệm của mỗi bất phương trình sau:
a) 3x + 5y < 15;
b) x – 2y ≥ 6;
c) y > – x + 3;
d) y ≤ 4 – 2x.
Lời giải:
a) Biểu diễn miền nghiệm của bất phương trình 3x + 5y < 15 gồm các bước sau:
+) Vẽ đường thẳng d: 3x + 5y = 15:
Đường thẳng d đi qua hai điểm (0; 3) và (5; 0).
+) Lấy điểm O(0; 0), ta có: 3.0 + 5.0 = 0 < 15.
Vậy miền nghiệm của bất phương trình đã cho là nửa mặt phẳng chứa điểm O(0; 0) và không kể đường thẳng d là nửa mặt phẳng tô màu trong hình sau:
b) Biểu diễn miền nghiệm của bất phương trình x – 2y ≥ 6 gồm các bước sau:
+) Vẽ đường thẳng d: x – 2y = 6:
Đường thẳng d đi qua hai điểm (0; – 3) và (6; 0).
+) Lấy điểm O(0; 0), ta có: 0 – 2.0 = 0 < 6.
Vậy miền nghiệm của bất phương trình đã cho là nửa mặt phẳng không chứa điểm O(0; 0) và kể cả đường thẳng d là nửa mặt phẳng tô màu trong hình sau:
c) Biểu diễn miền nghiệm của bất phương trình y > – x + 3 hay x + y > 3 gồm các bước sau:
+) Vẽ đường thẳng d: x + y = 3:
Đường thẳng d đi qua hai điểm (0; 3) và (3; 0).
+) Lấy điểm O(0; 0), ta có: 0 + 0 = 0 < 3.
Vậy miền nghiệm của bất phương trình đã cho là nửa mặt phẳng không chứa điểm O(0; 0) và không kể đường thẳng d là nửa mặt phẳng tô màu trong hình sau:
d) Biểu diễn miền nghiệm của bất phương trình y ≤ 4 – 2x hay 2x + y ≤ 4 gồm các bước sau:
+) Vẽ đường thẳng d: 2x + y = 4:
Đường thẳng d đi qua hai điểm (2; 0) và (0; 4).
+) Lấy điểm O(0; 0), ta có: 2.0 + 0 = 0 ≤ 4 .
Vậy miền nghiệm của bất phương trình đã cho là nửa mặt phẳng chứa điểm O(0; 0) và kể cả đường thẳng d là nửa mặt phẳng tô màu trong hình sau:
Bài 5: Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + 5y ≤ 10?
A. (5; 2).
B. (-1; 4).
C. (2; 1).
D. (-5; 6).
Lời giải:
Đáp án đúng là: C
Thay x = 4; y = 2 vào biểu thức 2x + 5y ta được 2 . 4 + 5. 2 = 18 > 10 nên phương án A không thỏa mãn.
Thay x = -1; y = 4 vào biểu thức 2x + 5y ta được 2 . (-1) + 5 . 4 = 18 > 10 nên phương án B không thỏa mãn.
Thay x = -5; y = 6 vào biểu thức 2x + 5y ta được 2 . (-5) + 5 . 6 = 20 > 10 nên phương án D không thỏa mãn.
Thay x = 2; y = 1 vào biểu thức 2x + 5y ta được 2 . 2 + 5 . 1 = 9 < 10 nên phương án C đúng.
Vậy ta chọn phương án C.
Bài 6: Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x - 3y > 13 ?
A. (1; -5).
B. (2; -4).
C. (3; -3).
D. (8; 1).
Lời giải:
Đáp án đúng là: D
Thay x = 1; y = -5 vào biểu thức 2x - 3y ta được 2 . 1 - 3 . (-5) = 17 > 13 nên phương án A không thỏa mãn.
Thay x = 2; y = -4 vào biểu thức 2x - 3y ta được 2 . 2 - 3 . (-4) = 16 > 13 nên phương án B không thỏa mãn.
Thay x = 3; y = -3 vào biểu thức 2x - 3y ta được 2 . 3 - 3 . (-3) = 15 > 13 nên phương án C không thỏa mãn.
Thay x = 8; y = 1 vào thức 2x - 3y ta được 2 . 8 - 3 . 1 = 13 nên phương án D đúng.
Vậy ta chọn phương án D.
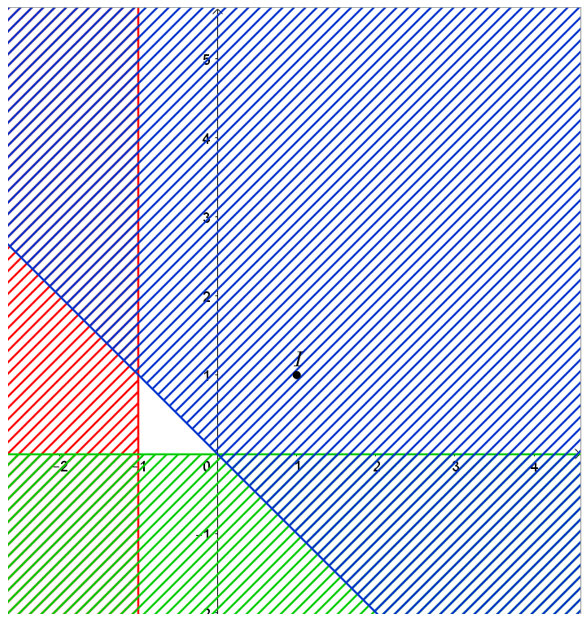
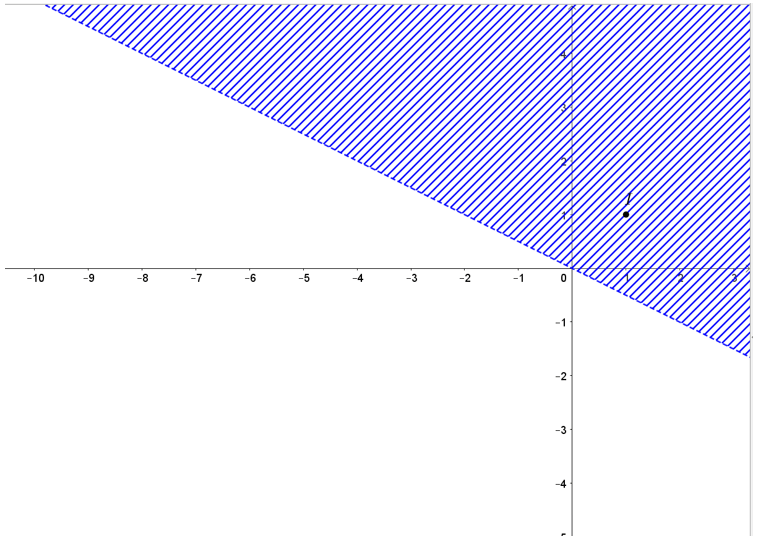
Bài 7:
Miền nghiệm của hệ bất phương trình
A. Một nửa mặt phẳng.
B. Miền tam giác.
C. Miền tứ giác.
D. Miền ngũ giác.
Lời giải:
Đáp án đúng là: B
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x = -1 là một đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng -1.
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x ta được 1 > -1.
Suy ra miền nghiệm của bất phương trình x ≥ -1 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Vẽ đường thẳng d2: x + y = 0 bằng cách vẽ một đường thẳng đi qua hai điểm (0; 0) và (-1; 1).
Chọn điểm I(1; 1) ∉d2 và thay vào biểu thức x + y ta được 1 + 1 = 2 > 0.
Suy ra miền nghiệm của bất phương trình x + y ≤ 0 là nửa mặt phẳng bờ d2 không chứa điểm I(1; 1).
• Đường thẳng d3: y = 0 trùng với trục Ox.
Chọn điểm I(1; 1) ∉ d3 và thay vào biểu thức y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d3 chứa điểm I(1; 1).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
Ta thấy miền nghiệm của hệ bất phương trình trên là miền tam giác.
Vậy chọn phương án B.
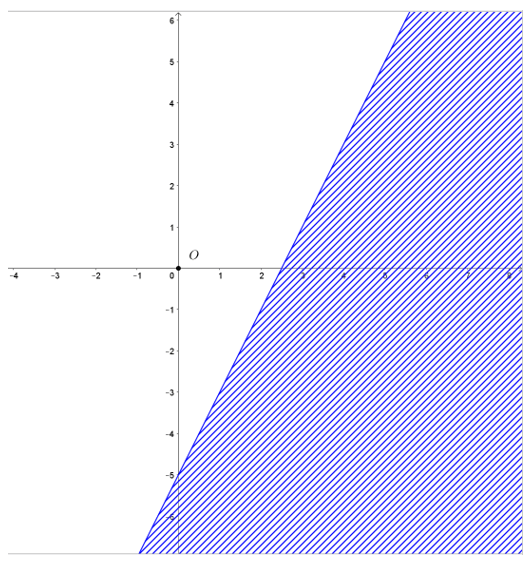
Bài 8:
Miền nghiệm của bất phương trình
A. Miền lục giác.
B. Miền tam giác.
C. Miền tứ giác.
D. Miền ngũ giác.
Lời giải:
Đáp án đúng là: D
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x + y = 1 bằng cách vẽ đường thẳng đi qua hai điểm (0; 1) và (1; 0).
Chọn điểm O(0; 0) ∉ d1 và thay vào biểu thức x + y được 0 < 1.
Suy ra miền nghiệm của bất phương trình x + y ≤ 1 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0).
• Đường thẳng d2: y = -3 là đường thẳng song song với trục Ox và đi qua điểm có hoành độ bằng -3.
Chọn điểm O(0; 0) ∉ d2 và thay vào biểu thức y được 0 > -3.
Suy ra miền nghiệm của bất phương trình y ≥ -3 là nửa mặt phẳng bờ d2 chứa điểm O(0; 0).
• Đường thẳng d3: y = 3 là đường thẳng song song với trục Ox và đi qua điểm có hoành độ bằng 3.
Chọn điểm O(0; 0) và thay vào biểu thức y được 0 < 3.
Suy ra miền nghiệm của bất phương trình y ≤ 3 là nửa mặt phẳng bờ d3 chứa điểm O(0; 0).
• Đường thẳng d4: x = -3 là đường thẳng song song với trục Oy và đi qua điểm có tung độ bằng -3.
Chọn điểm O(0; 0) ∉ d4 và thay vào biểu thức x được 0 > -3.
Suy ra miền nghiệm của bất phương trình x ≥ -3 là nửa mặt phẳng bờ d4 chứa điểm O(0; 0).
• Đường thẳng d5: x = 3 là đường thẳng song song với trục Oy và đi qua điểm có tung độ bằng 3.
Chọn điểm O(0; 0) và thay vào biểu thức x được 0 < 3.
Suy ra miền nghiệm của bất phương trình x ≤ 3 là nửa mặt phẳng bờ d5 chứa điểm O(0; 0).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
Ta thấy miền nghiệm của hệ là miền ngũ giác.
Vậy chọn phương án D.
Bài 9:
Miền nghiệm của hệ bất phương trình
A. Miền lục giác.
B. Miền tam giác.
C. Miền tứ giác.
D. Miền ngũ giác.
Lời giải:
Đáp án đúng là: C
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x + y = 10 bằng cách vẽ đường thẳng đi qua hai điểm (4; 6) và (5; 5).
Chọn điểm O(0; 0)∉ d1 và thay vào biểu thức x + y được 0 < 10.
Suy ra miền nghiệm của bất phương trình x + y ≤ 10 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0).
• Đường thẳng d2: y = -3 là đường thẳng song song với trục Ox và đi qua điểm có hoành độ bằng -3.
Chọn điểm O(0; 0) ∉ d2 và thay vào biểu thức y được 0 > -3.
Suy ra miền nghiệm của bất phương trình y ≥ -3 là nửa mặt phẳng bờ d2 chứa điểm O(0; 0).
• Đường thẳng d3: y = 3 là đường thẳng song song với trục Ox và đi qua điểm có hoành độ bằng 3.
Chọn điểm O(0; 0) và thay vào biểu thức y được 0 < 3.
Suy ra miền nghiệm của bất phương trình y ≤ 3 là nửa mặt phẳng bờ d3 chứa điểm O(0; 0).
• Đường thẳng d4: x = -3 là đường thẳng song song với trục Oy và đi qua điểm có tung độ bằng -3.
Chọn điểm O(0; 0) ∉ d4 và thay vào biểu thức x được 0 > -3.
Suy ra miền nghiệm của bất phương trình x ≥ -3 là nửa mặt phẳng bờ d4 chứa điểm O(0; 0).
• Đường thẳng d5: x = 3 là đường thẳng song song với trục Oy và đi qua điểm có tung độ bằng 3.
Chọn điểm O(0; 0) và thay vào biểu thức x được 0 < 3.
Suy ra miền nghiệm của bất phương trình x ≤ 3 là nửa mặt phẳng bờ d5 chứa điểm O(0; 0).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
Ta thấy miền nghiệm của hệ là miền tứ giác.
Vậy chọn đáp án C.
Bài 10: Biểu diễn miền nghiệm của các bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
a) x + y ≥ -4;
b) 2x - y ≤ 5;
c) x + 2y < 0;
d) -x + 2y > 0.
Lời giải:
a) Biểu diễn tập nghiệm của bất phương trình x + y ≥ -4 trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x + y = -4 bằng cách vẽ đường thẳng đi qua hai điểm (0; -4) và (-4; 0).
• Chọn điểm O(0; 0) ∉ d1 và thay vào biểu thức x + y ta được 0 > -4.
Suy ra miền nghiệm của bất phương trình x + y ≥ -4 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0).
b) Biểu diễn tập nghiệm của bất phương trình 2x - y ≤ 5 trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: 2x - y = 5 bằng cách vẽ đường thẳng đi qua hai điểm (0; -5) và (3; 1).
• Chọn điểm O(0; 0) ∉ d1 và thay vào biểu thức 2x - y ta được 0 < 5.
Suy ra miền nghiệm của bất phương trình 2x - y ≤ 5 là nửa mặt phẳng bờ d1 chứa điểm O(0; 0).
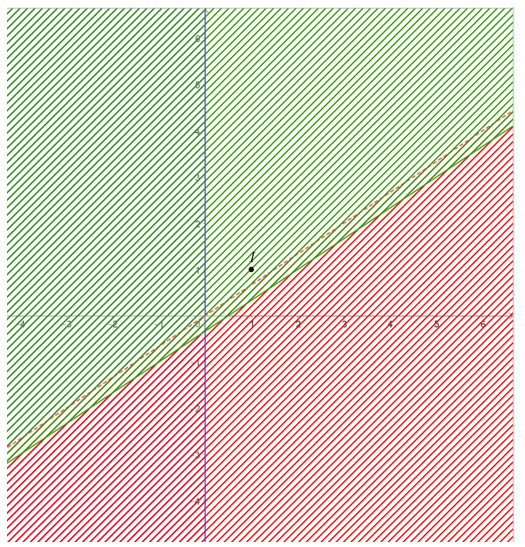
c) Biểu diễn tập nghiệm của bất phương trình x + 2y < 0 trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: x + 2y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (2; -1).
Chọn điểm I(1; 1)∉ d1 và thay vào biểu thức x + 2y ta được 1 + 2 . 1 = 3 > 0.
• Suy ra miền nghiệm của bất phương trình x + 2y < 0 là nửa mặt phẳng bờ d1 không chứa điểm I(1; 1) và bỏ đi đường thẳng d1.
d) Biểu diễn tập nghiệm của bất phương trình -x + 2y > 0 trên mặt phẳng tọa độ:
• Vẽ đường thẳng d1: -x + 2y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (2; 1).
• Chọn điểm I(1; 1)∉d1 và thay vào biểu thức -x + 2y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình -x + 2y > 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1) và bỏ đi đường thẳng d1.
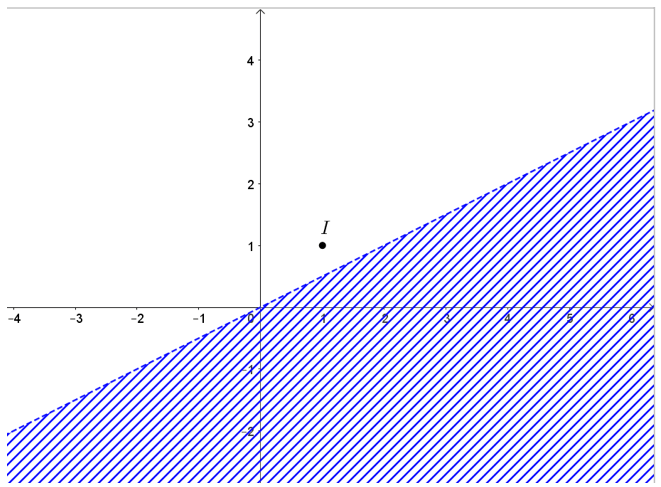
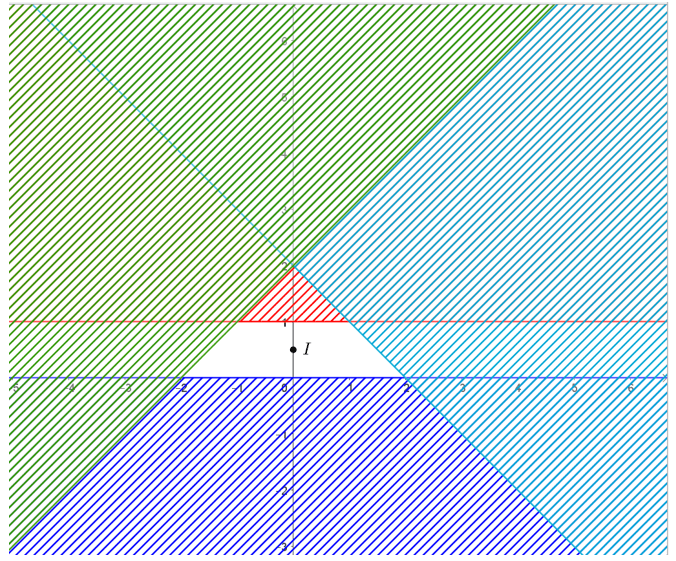
Bài 11: Biểu diễn miền nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
Lời giải:
a) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1)∉ d1 và thay vào biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Đường thẳng d2: x = 10 là đường thẳng song song với trục Oy và đi qua điểm có hoành độ bằng 10.
Chọn điểm I(1; 1) ∉ d2 và thay vào biểu thức x ta được 1 < 10.
Suy ra miền nghiệm của bất phương trình x ≤ 10 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1).
• Đường thẳng d3: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(1; 1) ∉ d3 và thay vào biểu thức y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình y > 0 là nửa mặt phẳng bờ d3 chứa điểm I(1; 1) và bỏ đi đường thẳng d3.
• Vẽ đường thẳng d4: x - y = 4 bằng cách vẽ đường thẳng đi qua hai điểm (4; 0) và (0; -4).
Chọn điểm I(1; 1) ∉ d4 và thay vào biểu thức x - y ta được 0 < 4.
Suy ra miền nghiệm của bất phương trình x - y > 4 là nửa mặt phẳng bờ d4 không chứa điểm I(1; 1) và bỏ đi đường thẳng d4.
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
b) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(0; 0,5) Ï d1 và thay vào biểu thức y ta được 0,5 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(0; 0,5).
• Đường thẳng d2: y = 1 là đường thẳng song song với trục Ox và đi qua điểm có tung độ bằng 1.
Chọn điểm I(0; 0,5) ∉ d2 và thay vào biểu thức y ta được 0,5 < 1.
Suy ra miền nghiệm của bất phương trình y ≤ 1 là nửa mặt phẳng bờ d2 chứa điểm I(0; 0,5).
• Vẽ đường thẳng d3: x + y = 2 bằng cách vẽ đường thẳng đi qua hai điểm (2; 0) và (0; 2).
Chọn điểm I(0; 0,5) ∉ d3 và thay vào biểu thức x + y ta được 0,5 < 2.
Suy ra miền nghiệm của bất phương trình x + y ≤ 2 là nửa mặt phẳng bờ d3 chứa điểm I(0; 0,5).
• Vẽ đường thẳng d4: y - x = 2 bằng cách vẽ đường thẳng đi qua hai điểm (0; 2) và (-2; 0).
Chọn điểm I(0; 0,5) ∉ d4 và thay vào biểu thức y - x ta được 0,5 < 2.
Suy ra miền nghiệm của bất phương trình y - x ≤ 2 là nửa mặt phẳng bờ d4 chứa điểm I(0; 0,5).
Khi đó miền nghiệm của hệ là miền không bị gạch như hình vẽ dưới đây:
c) Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1) ∉ d1 và thay vào biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Vẽ đường thẳng d2: 4x - 6y = 0 bằng cách vẽ đường thẳng đi qua hai điểm (0; 0) và (3; 2).
Chọn điểm I(1; 1)∉d2 và thay vào biểu thức 4x - 6y ta được -2 < 0.
Suy ra miền nghiệm của bất phương trình 4x - 6y < 0 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1) và bỏ đi đường thẳng d2.
• Vẽ đường thẳng d3: 2x - 3y = 1 bằng cách vẽ đường thẳng đi qua hai điểm (2; 1) và (5; 3).
Chọn điểm I(1; 1) ∉ d3 và thay vào biểu thức 2x - 3y ta được -1 < 1.
Suy ra miền nghiệm của bất phương trình 2x - 3y ≥ 1 là nửa mặt phẳng bờ d3 không chứa điểm I(1; 1).
Khi đó hệ vô nghiệm vì mặt phẳng tọa độ đều bị gạch.
Xem thêm các dạng bài tập hay, có đáp án:
60 Bài tập về Phương trình mũ và phương trình logarit (có đáp án năm 2024)
60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024)
50 Bài tập Phương trình quy về phương trình bậc hai (có đáp án năm 2024)
100 Bài tập về Phương trình quy về phương trình bậc hai (có đáp án năm 2024)
500 Bài tập bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2024)