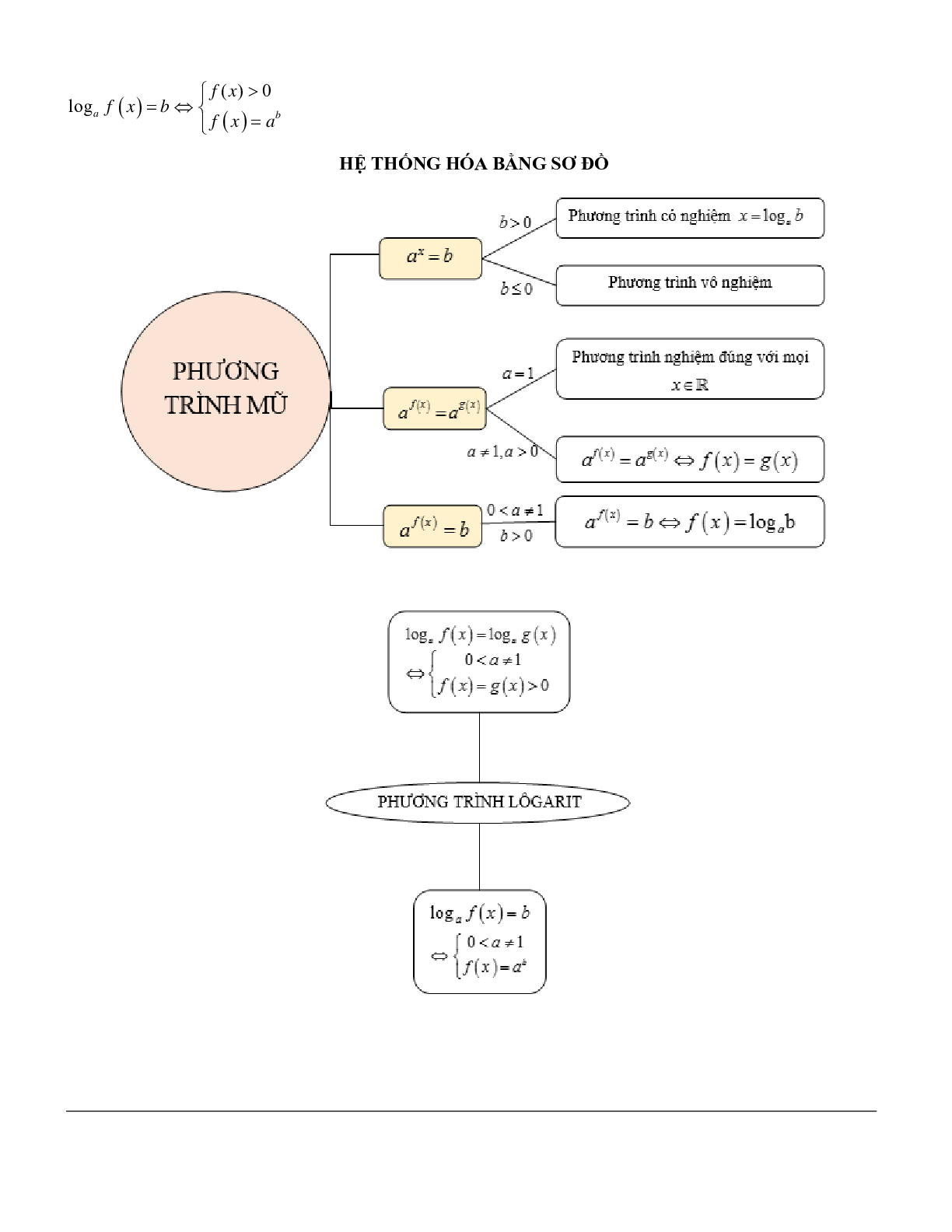
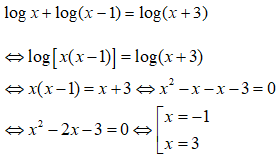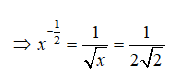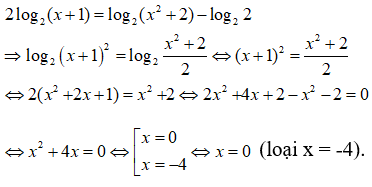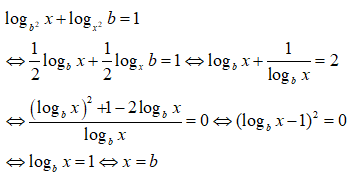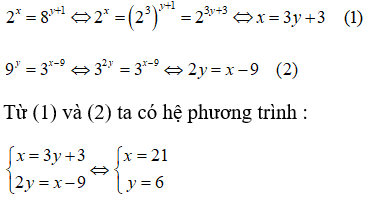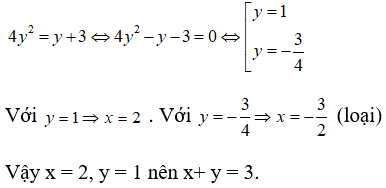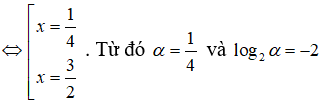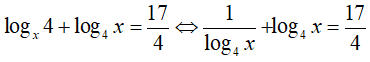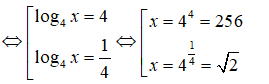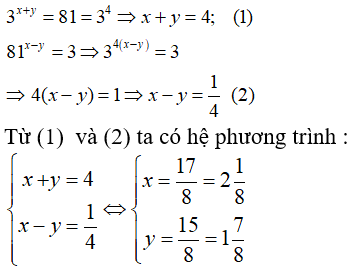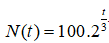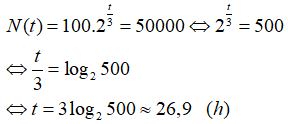Phương trình mũ và phương trình logarit
Kiến thức cần nhớ
1. Phương trình mũ
1.1. Phương trình mũ cơ bản
– Phương trình mũ cơ bản có dạng: ax = b (a > 0; a ≠ 1).
Để giải phương trình trên, ta sử dụng định nghĩa logarit.
Với b > 0 ta có: ax = b⇔x = logab.
Với b ≤ 0, phương trình vô nghiệm.
– Minh họa bằng đồ thị
Hoành độ giao điểm của đồ thị hai hàm số y = ax và y = b là nghiệm của phương trình ax = b.
Số nghiệm của phương trình là số giao điểm của hai đồ thị.
Rõ ràng, nếu b ≤ 0 thì hai đồ thị không cắt nhau nên phương trình vô nghiệm.
Nếu b > 0 ta có hai đồ thị như hình dưới đây. Trên mỗi hình, hai đồ thị luôn cắt nhau tại một điểm nên phương trình có nghiệm duy nhất.
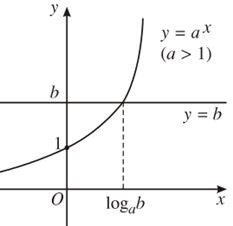
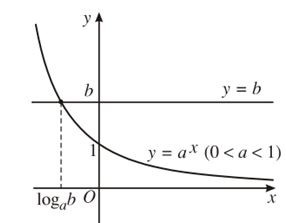
Kết luận:
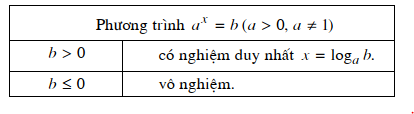
– Ví dụ 1. Giải phương trình 2x + 1 + 2x + 2 = 16.
Lời giải:
Ta có: 2x + 1 + 2x + 2 = 16.
⇔2.2x + 4.2x = 16
⇔6.2x = 16
⇔2x = 83⇔x = log283
Vậy x=log283.
1.2. Cách giải một số phương trình mũ cơ bản
a) Đưa về cùng cơ số.
– Ví dụ 2. Giải phương trình 3x+ 2 = (13)6−2x
Lời giải:
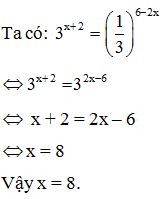
b) Đặt ẩn phụ
– Ví dụ 3. Giải phương trình 4x – 5. 2x + 6 = 0
Lời giải:
Đặt t = 2x (với t > 0)
Phương trình đã cho trở thành: t2 – 5t + 6 = 0
⇔[t=2t=3 ⇒[2x= 2 ⇒x= 12x = 3⇒x = log23
Vậy phương trình đã cho có 2 nghiệm là x = 1 và x = log23.
c) Logarit hóa.
– Ví dụ 4. Giải phương trình: 3x. 5x2 =1
Lời giải:
Lấy logarit cơ số 3 hai vế ta được:
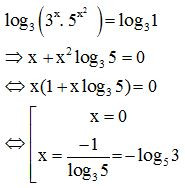
Vậy phương trình đã cho có 2 nghiệm là x = 0 và x = – log53.
2. Phương trình logarit
– Phương trình logarit là phương trình có chứa ẩn số trong biểu thức dưới dấu logarit.
– Ví dụ 5. Các phương trình log2x=4;log23x+2log4x=0… đều là phương trình logarit.
2.1. Phương trình logarit cơ bản
– Phương trình logarit cơ bản có dạng: logax = b (a > 0; a ≠ 1).
Theo định nghĩa logarit ta có:
logax = b⇔x = ab
– Minh họa bằng đồ thị
Vẽ đồ thị hàm số y = loga x và đường thẳng b trên cùng một hệ tọa độ.
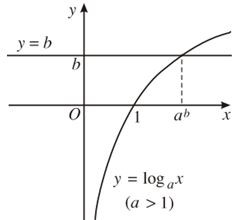
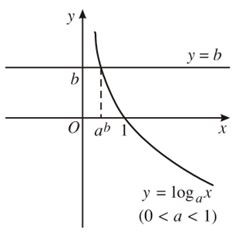
Trong cả hai trường hợp, ta đều thấy đồ thị của các hàm số y = logax và đường thẳng y = b luôn cắt nhau tại một điểm với mọi b∈R
Kết luận: Phương trình logax = b (a > 0; a ≠ 1) luôn có nghiệm duy nhất x = ab với mọi b.
2.2. Cách giải một số phương trình logarit đơn giản
a) Đưa về cùng cơ số
Ví dụ 6. Giải phương trình log3x + log9x = 6.
Lời giải:
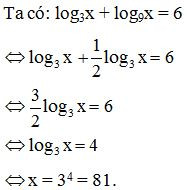
Vậy nghiệm của phương trình đã cho là x = 81.
b) Đặt ẩn phụ
– Ví dụ 7. Giải phương trình log25x +3log5x =0
Lời giải:
Đặt t =log5x, phương trình đã cho trở thành:
t2 + 3t = 0 nên t = 0 hoặc t = –3.
Với t = 0 thì log5x = 0 nên x = 1.
Với t = –3 thì log5x = –3 nên x = 5–3.
Vậy phương trình đã cho có 2 nghiệm là x = 1 và x = 5–3.
c) Mũ hóa
– Ví dụ 8. Giải phương trình: log3(90 – 3x) = x + 2
Lời giải:
Điều kiện của phương trình là 90 – 3x > 0.
Phương trình đã cho tương đương với:
90 – 3x = 3x + 2 hay 90 – 3x = 9.3x
⇔10.3x = 90
⇔3x = 9 nên x = 2 (thỏa mãn điều kiện)
Vậy nghiệm của phương trình đã cho là x = 2.
Các dạng bài tập về phương trình mũ và phương trình logarit
(Xem thêm các dạng bài tập trong file pdf)
Dạng 1. Phương pháp đưa về cùng cơ số.
Dạng 2. Phương pháp đặt ẩn phụ.
Dạng 3. Phương pháp logarit hóa, mũ hóa.
Dạng 4. Phương pháp biến đổi thành tích.
Dạng 5. Phương pháp sử dụng tính đơn điệu.
Bài tập có hướng dẫn
1. Bài tập vận dụng
Bài 1: Giải phương trình logx = log(x + 3) - log(x - 1)
Lời giải:
Điều kiện x > 1. Khi đó phương trình tương đương với
Loại nghiệm x = -1 do không thỏa mãn điều kiện. Phương trình có một nghiệm x = 3.
Chú ý: Cũng như ở ví dụ 5, sai lầm học sinh dễ gặp bài này là do chủ quan muốn tiết kiệm thời gian mà quên đặt điều kiện, dẫn tới không loại được nghiệm x = -1 và chọn phương án nhiễu D.
Bài 2: Nếu log7(log3(log2x)) = 0 thì x-12 bằng :
Lời giải:
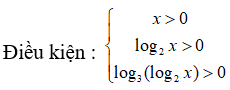
log7(log3(log2x)) = 0 ⇔ log3(log2x) = 70 = 1
⇔ log2x = 3t ⇔ x = 23 = 8
Bài 3: Giải phương trình log√2(x + 1) = log2(x2 + 2) - 1
Lời giải:
Điều kiện x > -1. Khi đó phương trình tương đương với
2log2(x + 1) = log2(x2 + 2)
Bài 4: Cho biết logb2x + logx2b = 1, b > 0, b ≠ 1, x ≠ 1. Khi đó x bằng?
Lời giải:
Điều kiện: x > 0
Chú ý. Khác với các ví dụ trên, các biến đổi trong ví dụ này không làm mở rộng miền xác định của phương trình (x > 0). Do đó ta đã không nhất thiết phải đặt điều kiện x > 0. Trong nhiều trường hợp việc bỏ qua đặt điều kiện sẽ làm đơn giản hơn và tiết kiệm thời gian.
Bài 5: Cho biết 2x = 8y + 1 và 9y = 3x - 9 . Tính giá trị của x + y
Lời giải:
Vậy x + y =27.
Bài 6: Giả sử x, y là hai số thực thỏa mãn đồng thời 3x2 - 2xy = 1 và 2log3x = log3(y + 3). Tính x + y
Lời giải:
Điều kiện x > 0, y > -3.
Ta có: 3x2 - 2xy = 1 = 30 ⇔ x2 - 2xy = 0
⇔ x(x - 2y) = 0 ⇔ x - 2y = 0 (x > 0) ⇔ x = 2y (1)
2log3x = log3( y + 3) ⇔ log3x2 = log3(y + 3) ⇔ x2 = y + 3 (2)
Thế (1) vào (2) ta được:
Bài 7: Giả sử α và β là hai nghiệm của phương trình 3 + 2log2x = log2(14x - 3). Khẳng định nào sau đây là đúng ?
Lời giải:
Trước hết, ta giải phương trình 3 + 2log2x = log2(14x - 3) (1)
Điều kiện x > 314. Khi đó (1) <=7gt; log28 + log2x2 = log2(14x - 3)
⇔ 8x2 = 14x - 3 ⇔ = 8x2 - 14x + 3 = 0
Bài 8: Tính tích các nghiệm của phương trình logx4 + log4x = 174
Lời giải:
Điều kiện : x > 0 ; x ≠ 1
Đặt t = log4x, nhận được phương trình:
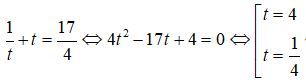
Tích hai nghiệm : 256.√2
Bài 9: Tìm hai số x và y đồng thời thỏa mãn 3x + y = 81 và 81x - y = 3
Lời giải:
Bài 10: Một quần thể vi khuẩn bắt đầu từ 100 cá thể và cứ sau 3 giờ thì số cá thể lại tăng gấp đôi. Bởi vậy, số cá thể vi khuẩn được biểu thị theo thời gian t (tính bằng giờ) bằng công thức
Hỏi sau bao lâu thì quần thể này đạt đến 50000 cá thể (làm tròn kết quả đến hàng phần mười) ?
Lời giải:
Sau t giờ thì số cá thể vi khuẩn có được là :
2. Bài tập tự luyện có hướng dẫn
(Xem thêm các bài tập trong file pdf)
Xem thêm các dạng bài tập Toán chi tiết và hay khác:
60 Bài tập về Hàm số lũy thừa (có đáp án năm 2023)
60 Bài tập về Lôgarit (có đáp án năm 2023)
60 Bài tập về Bất phương trình mũ và bất phương trình logarit (có đáp án năm 2023)